题21
题目
[!question]+
(21) (本题满分 11 分)
已知函数
分析
[!NOTE]+
没读懂这个题目,我在考虑对称性的事情,但是实际上不是,因为这里没有具体可以拿出来对称的函数
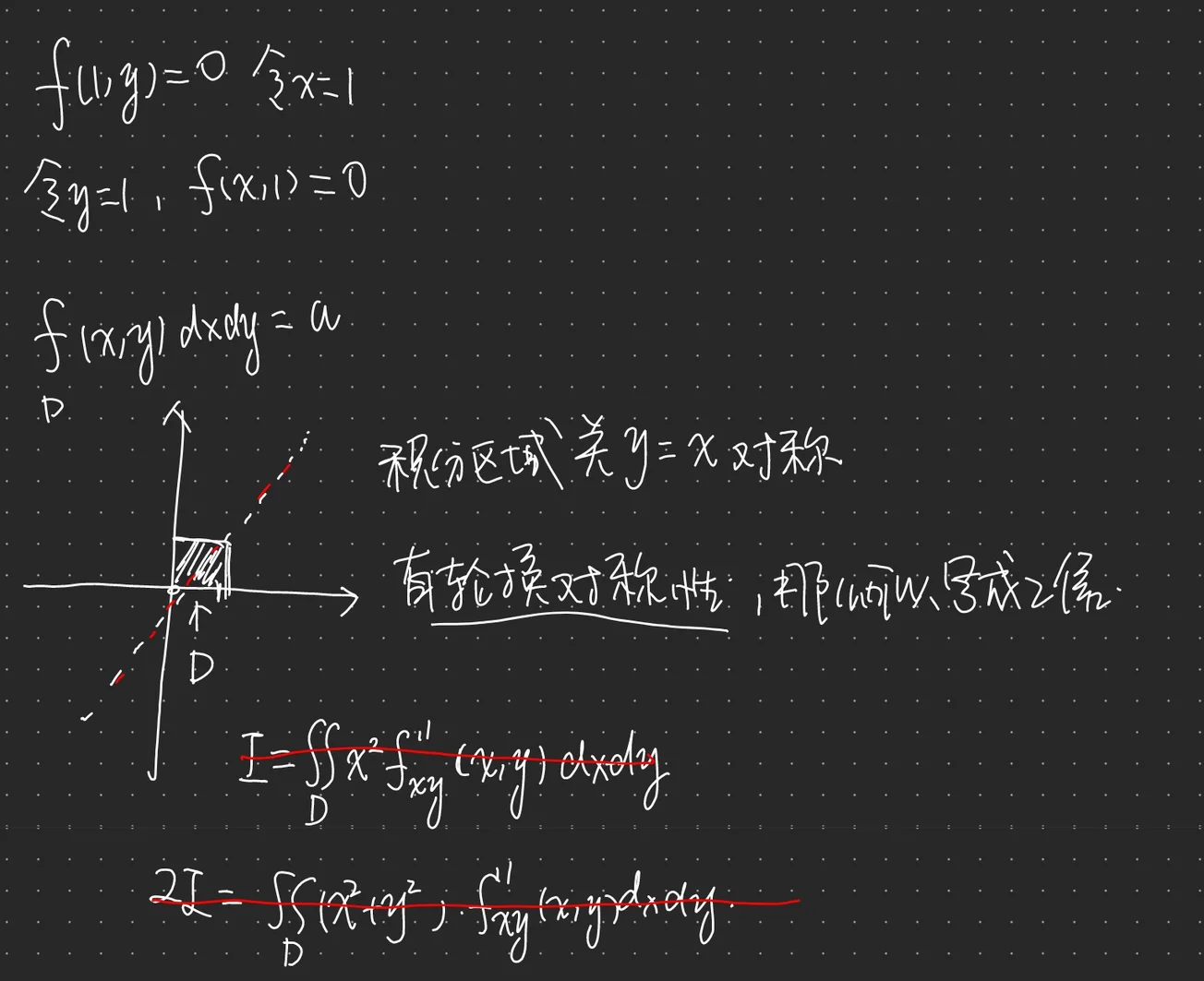
解
[!done]-

一般来说,给定一个二重积分
(解) 由于
由于
从而,
Jun 19, 20253 min read
[!question]+
(21) (本题满分 11 分)
已知函数
[!NOTE]+
没读懂这个题目,我在考虑对称性的事情,但是实际上不是,因为这里没有具体可以拿出来对称的函数

[!done]-

一般来说,给定一个二重积分
(解) 由于
由于
从而,