题5

题5

题目

[!error]+
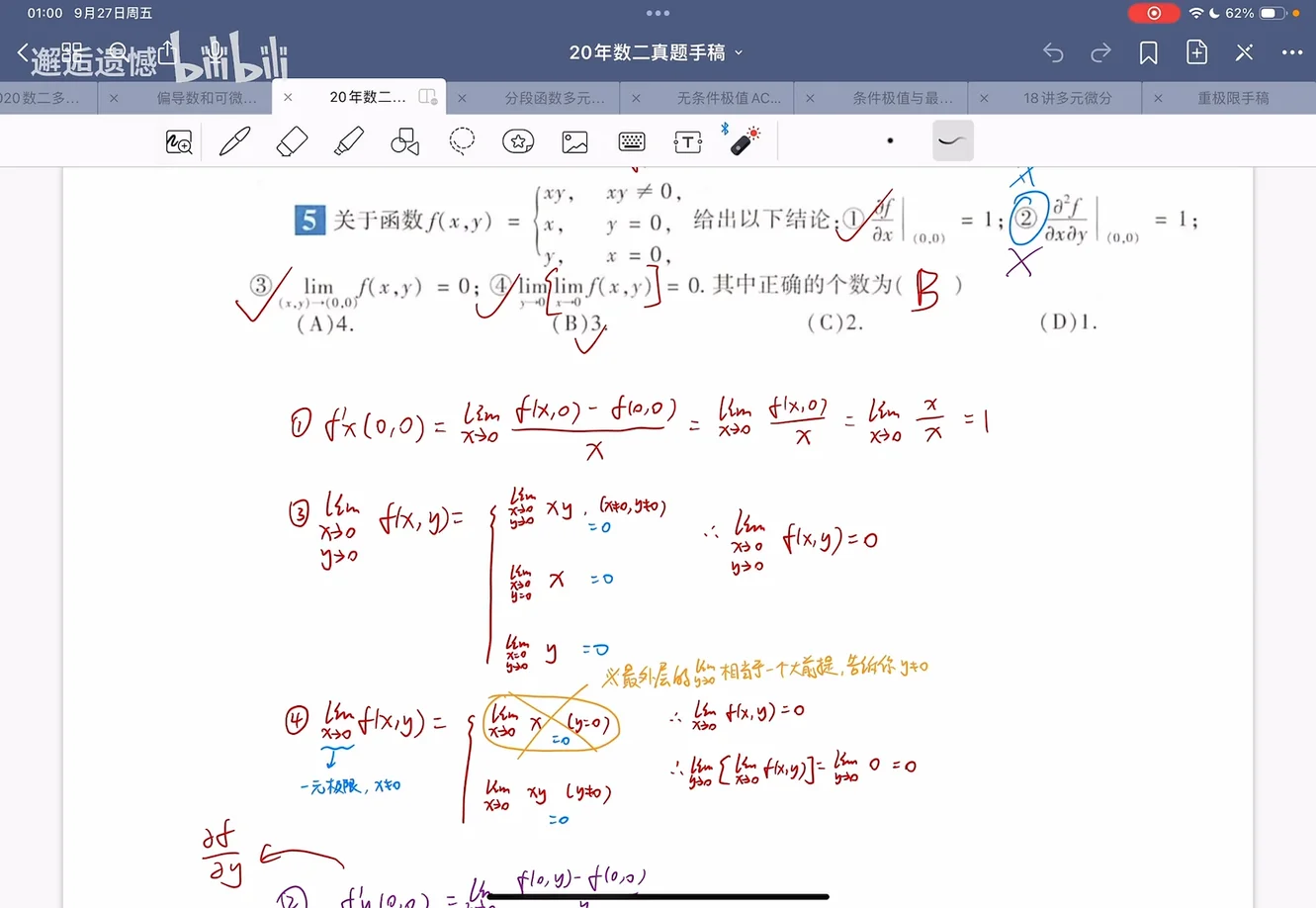
关于函数 ，给出以下结论：
① ；
② ；
③ ；
④ .
其中正确的个数为 ( )
(A) 4.
(B) 3.
(C) 2.
(D) 1.

分析

[!NOTE]+
邂逅遗憾认为是考研历史上多元函数的极限中最难的一道，关键是第二个命题的混合偏导数，这里分段了，不要拿公式直接求导，用定义式
第四个命题中外层的如何理解？
最外层的相当于一个大前提，告诉你

现在重新做，又忘记了

多元分段函数偏导用定义

解

[!done]-
二元函数的极限 设二元函数 的定义域为 , 是 的聚点. 若存在常数 , 对于任意给定的正数 , 总存在正数 , 使得当点 时, 都有

成立, 则称常数 为函数 当 时的极限, 记作 . 二元函数的极限也叫做二重极限.

二元函数的偏导数 设函数 在点 的某一邻域内有定义, 当 固定在 而 在 处有增量 时, 相应的函数有增量 , 若

存在,则称此极限为函数 在点 处对 的偏导数,记作 或 .

解 根据偏导数的定义,

① 正确.

根据偏导数的定义,

但是根据定义,当 时,

不存在, 当然也不存在.

② 不正确.

根据 的定义,

• 当 时, ,当 时,

• 当 时, ;

• 当 时, .

而 ,故 .

③ 正确.

按照累次极限的顺序,先计算 ,再计算 . 根据累次极限的定义,只需考虑 的情况.

④ 正确.

因此,共有 3 个结论正确,应选 B.