https://www.bilibili.com/video/BV1fH4y1f7bR?t=4.9
AB可交换,AB都可以做相似对角化,而且是同一个可逆矩阵P的作用下实现的,在例8.13中证明了它,在例8.12中运用了
Q:AB的矩阵乘法,可以写成他们的线性组合,那么
A:AB可交换前后顺序
结论1:无论可变换与否,
Q:下面称作西尔维斯特定理
结论2:更进一步,若
A:
当
定理的证明是显然的,注意到:
两侧取行列式,定理得证。
Q:能够得到矩阵可交换的常用条件:
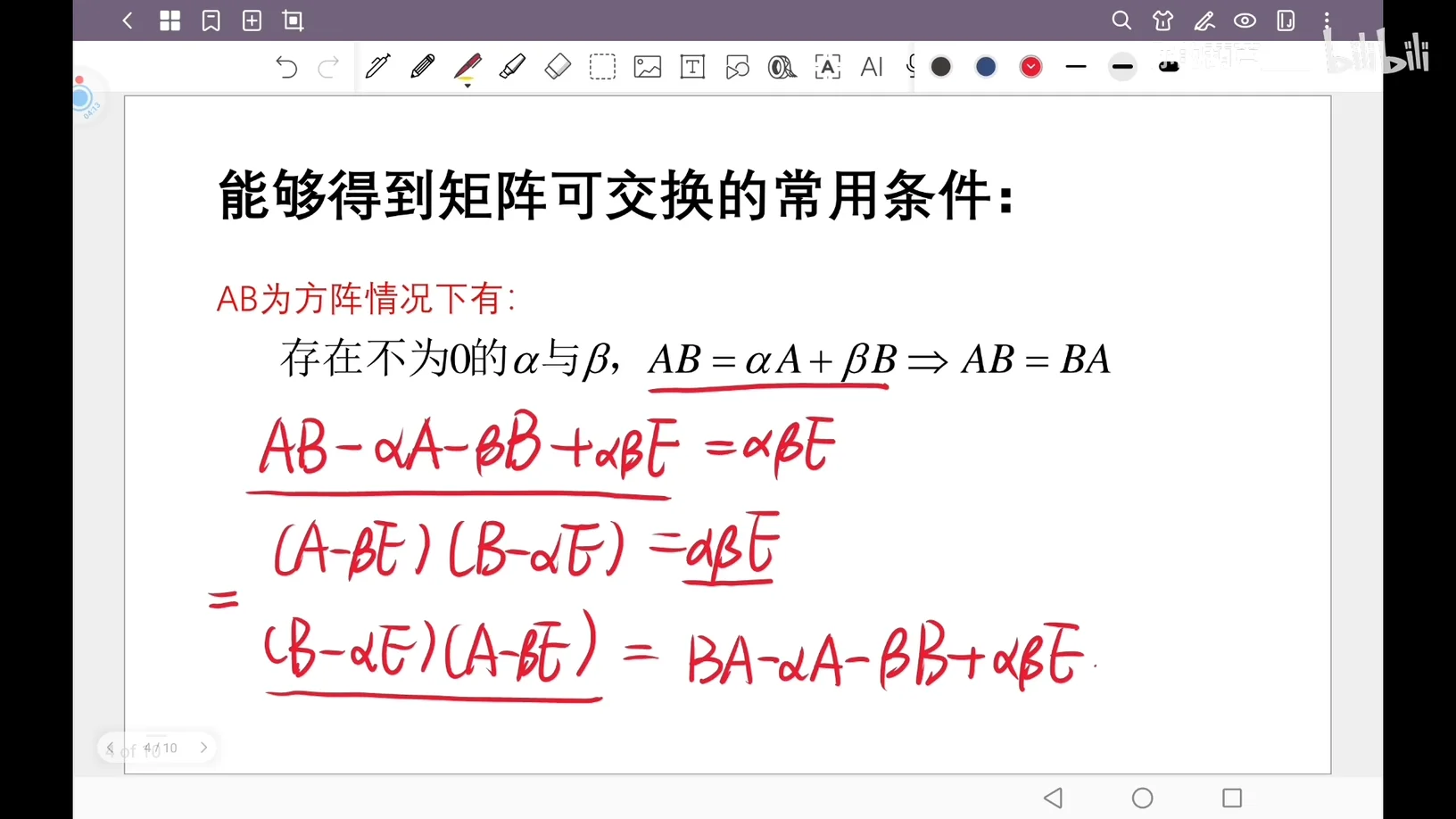
A:存在不为
上面这个条件A和B可以分解开组合起来,可以得到AB是可交换的,但是反过来,由可交换是不能得到AB可以拆开的这个条件的
Q:可交换矩阵的特征值、特征向量关系
A、B为n阶方阵,且AB=BA,则有:
A:(注:1需要掌握,2、3可作为拓展视情况而定)
- A与B存在公共特征向量,注意,只是说有相同的,不是全都是一样的
- 对A的任一
- 对AB的任一
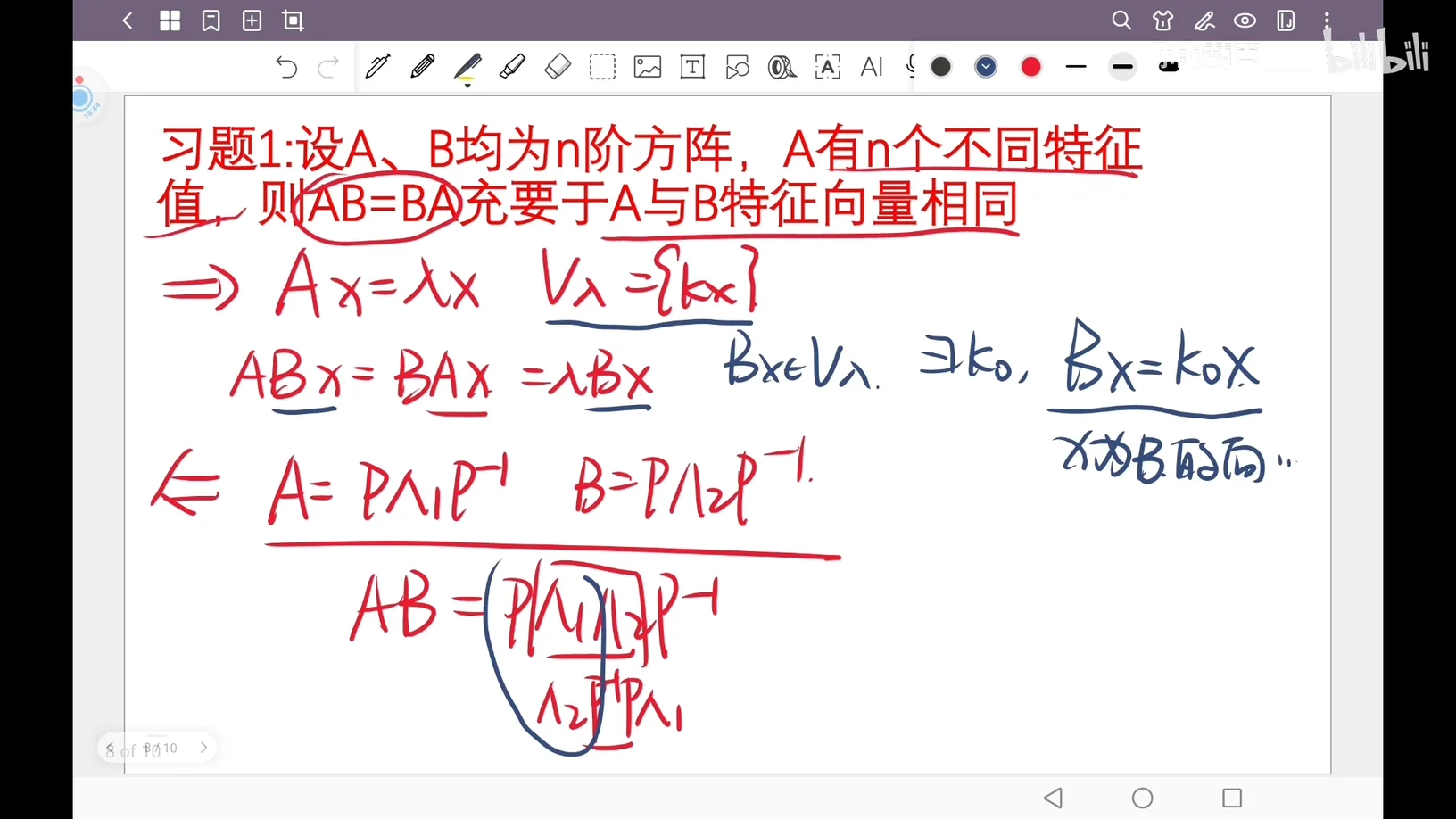
Q:习题 1:设
A:我们要证明的是:如果
(1) 必要性:
(2) 充分性:
3. 分步推理:
(1) 必要性:
- 假设:
- 目标: 证明
- 推理过程:
- 设
- 对等式两边左乘
- 由于
- 因此,我们有
- 由于
- 这意味着
- 由于
(2) 充分性:
- 设
- 假设:
- 目标: 证明
- 推理过程:
- 由于
- 由于
- 现在,我们可以计算
- 由于对角矩阵的乘法满足交换律,所以
- 因此,我们得到
- 由于
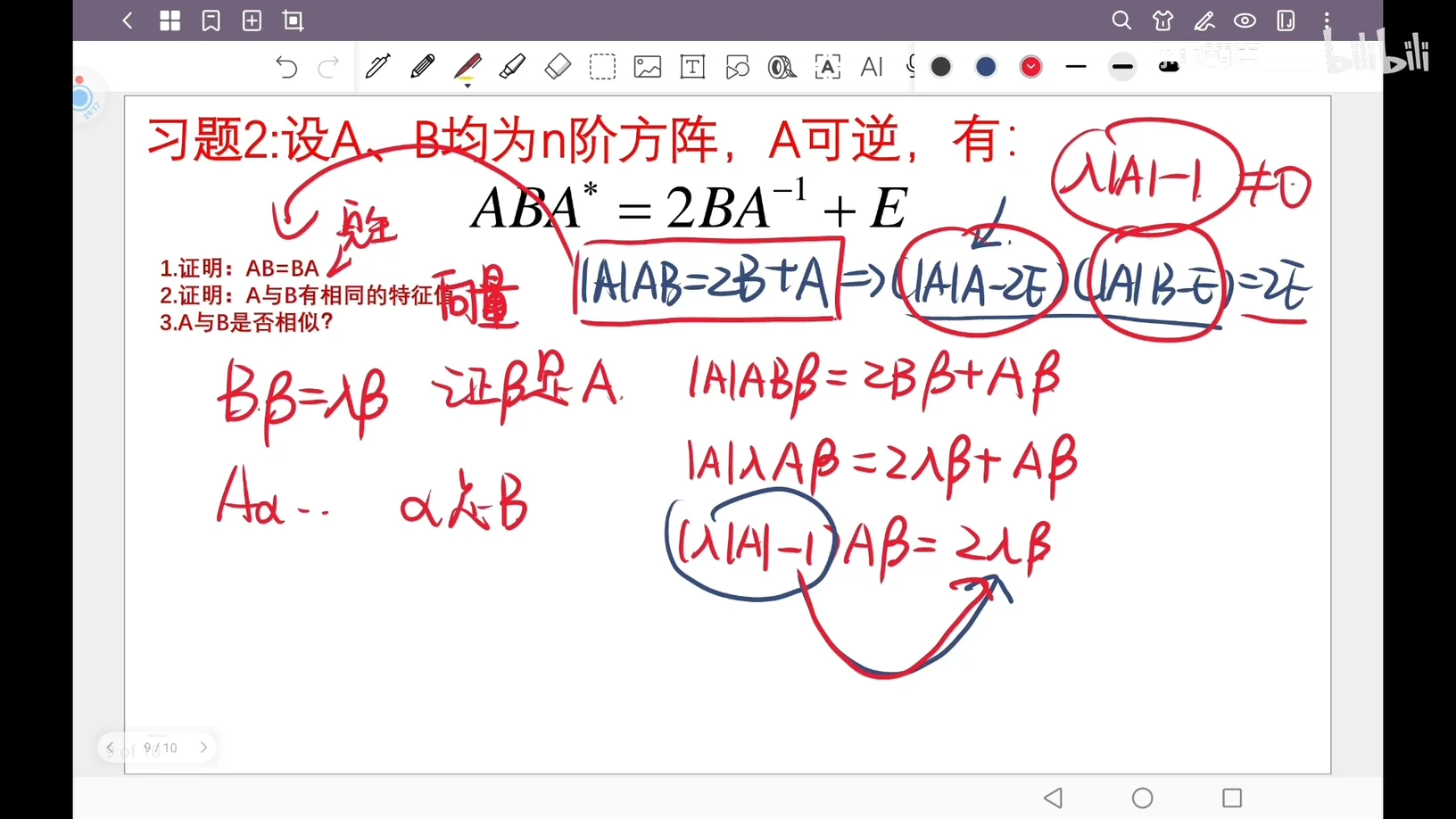
习题 2: 设
- 证明:
- 证明:
判断左边的系数不为0,除到右边来就得到了定义的形式