例2.18
题目
Q:设函数
①若
②若
正确的选项是 ( ).
(A) 仅①正确
(B) 仅②正确
(C) ①②都正确
(D) ①②都错误
分析
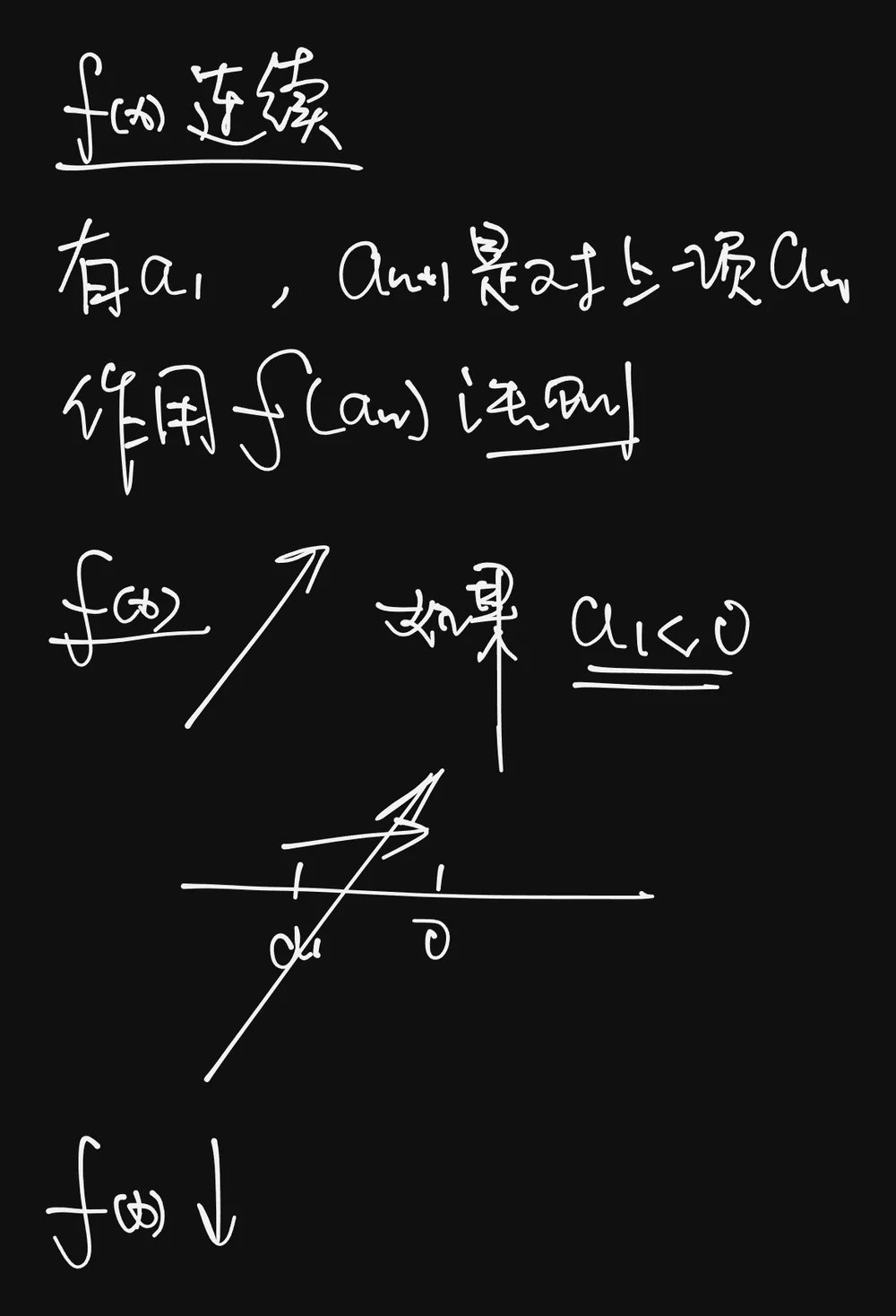
A:最好思考的方向应该是,设置一个单调增有上界的函数,手动模拟一个,然后再设置一些a1…an带进去具体的函数再看
但是一时之间,脑袋里面没有想到什么函数是这样的
- 01:10

严格单增加有上界,这是右侧的顶端,而在0的左侧,有是越增加越小的,也就是所谓的增长是要看方向和起点的
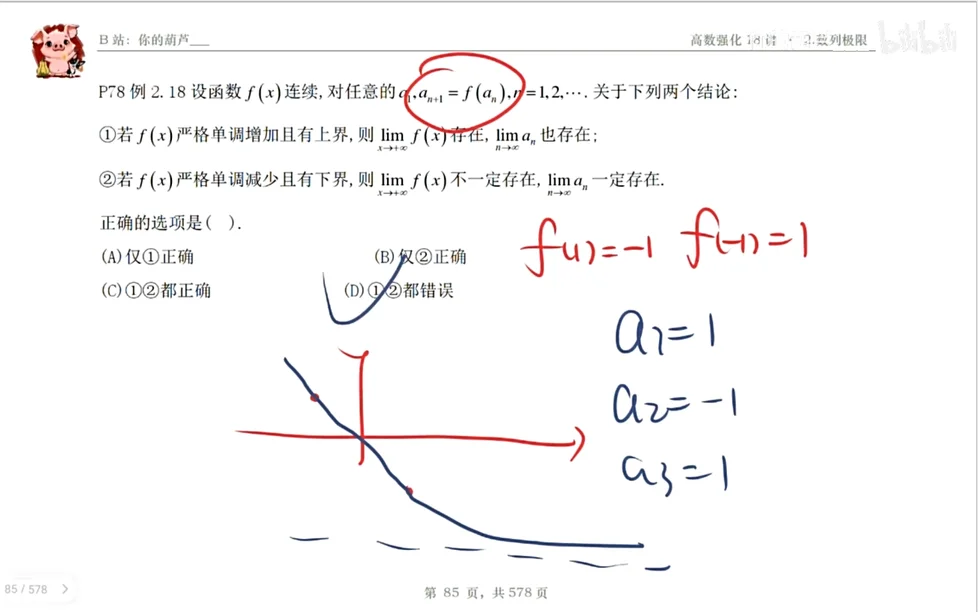
第二个的核心思想在于,数列是离散的,可以把它卡在某些点上面反复跳,而不影响作用法则在整个坐标轴上的表现
解
应选(D).
对于①,取
令
对于②,取
令
【注】(1) 解析中所取的两个反例说明了两种
①
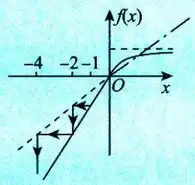
(a)
②
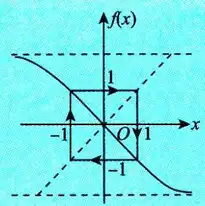
(b)
(2)对于