题19

题19

题目

[!question]+
将长为 的铁丝分成三段,依次围成圆、正方形与正三角形. 三个图形的面积之和是否存在最小值?若存在,求出最小值.

分析

[!NOTE]+
拉格朗日乘数法记得算出来驻点以后，驻点之间比较可以知道区域内谁是极大值极小值，同时再和区域边界上的值做比较，才能判断为约束下的最值

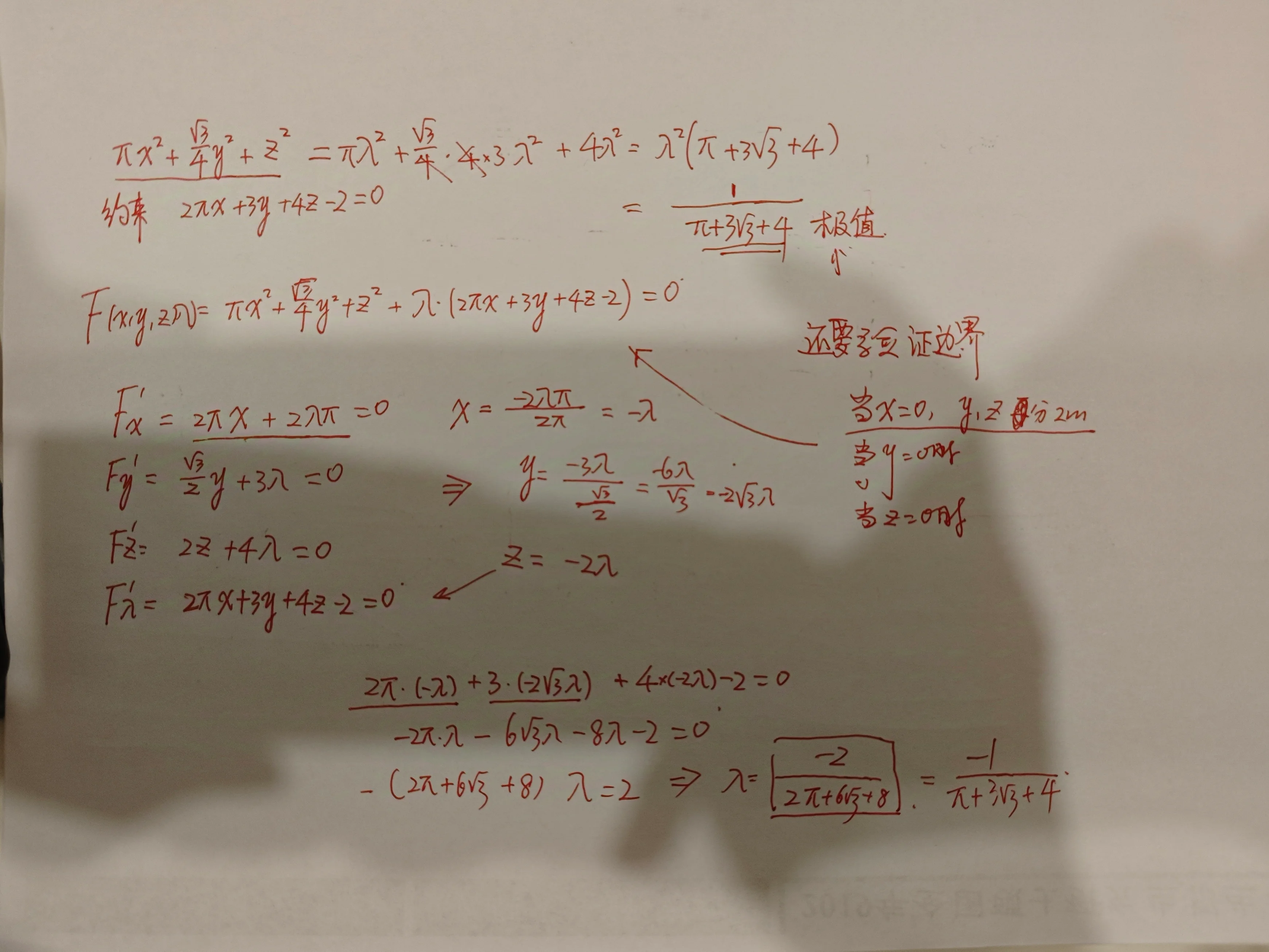
解

[!done]-
本题为一个实际问题，应先根据题意建立目标函数，即三个图形的面积之和，并写出约束条件。圆、正方形、正三角形的面积分别为其半径、边长、边长的函数，而圆的半径、正方形的边长、正三角形的边长可用它们的周长表示，从而可以用圆、正方形、正三角形的周长作为变量建立目标函数。

解：设圆、正方形、正三角形的周长分别为 ，则圆的半径 ，正方形的边长 ，正三角形的边长 。于是，三个图形的面积之和为

.

由于三段铁丝的周长之和为 2，故 。

建立拉格朗日函数 。

令

由前三个方程可得 。

代入 可得

.

于是，。

将所得 的值代入 可得

.

为了判定所求得可能的极值点是否为最小值点，我们把问题转化为目标函数 在有界闭区域 上的最值问题。

由于连续函数在有界闭区域上一定能取到最值，故若我们能分别计算出 在边界 上的最值，再与 比较，则所得最小值即为区域 上的最小值。

当 时， 在 下的最小值为 。

当 时， 在 下的最小值为 。

当 时， 在 下的最小值为 。

4 个值比较可得， 为整个区域 上的最小值，也为 时的 的最小值。三个图形的面积之和存在最小值，最小值为 。

注：本题也可以将目标函数写为圆的半径 、正方形的边长 、正三角形的边长 的函数，从而目标函数为 ，约束条件为 。利用拉格朗日乘数法可求得拉格朗日函数 的唯一驻点。