邻接表

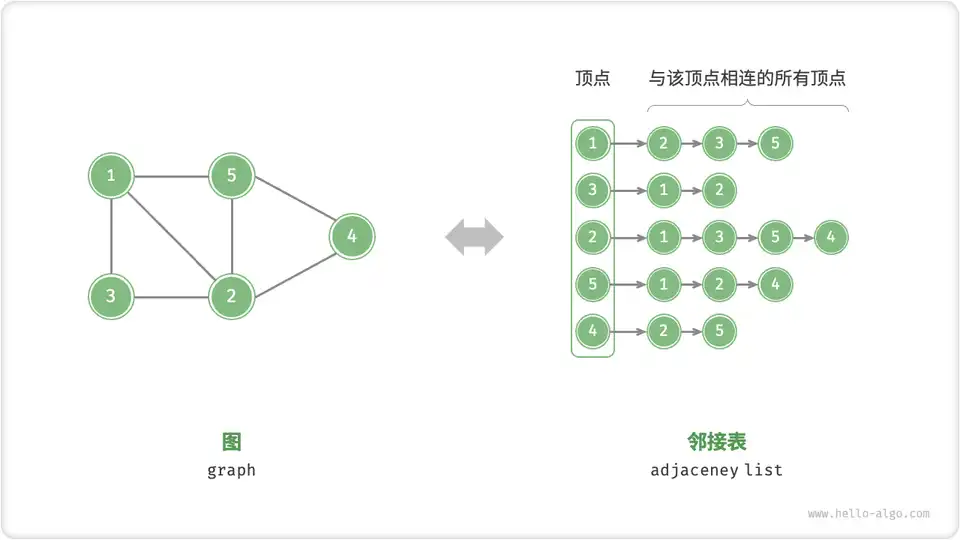
邻接表存储的是点，存每一个点的相邻点，和他们的边权
每一个点用 表示， 是一个集合，用结构体来表示相邻点和这个边权

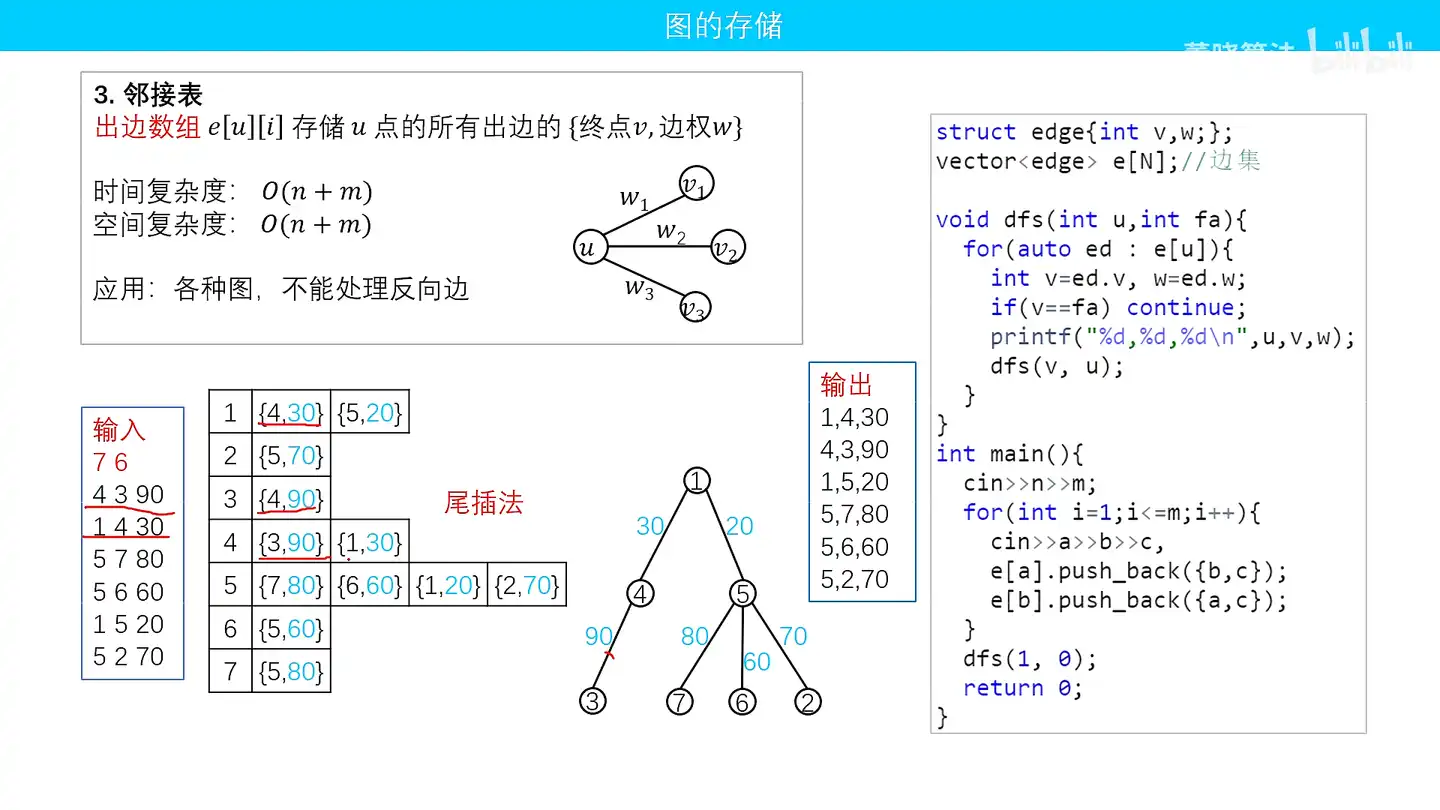
比如 是点4，，e是出边数组这个数据集合，这个4号点下有很多的数据，也就是它的出边，比如3和1，也就是这个数组的

领接表存两次

注意！因为点只知道，自己去向哪里，不知道谁要进入自己，所以，一组 点边点 需要正反存储两次，分别表示入度和出度。
e[a].push_back({b,c}) 这是正向的存储 4 3 90
e[b].push_back({a,c}) 这是反向的存储 3 4 90

邻接表的复杂度

• 时间复杂度：添加边和查询边的操作为 ，其中 是顶点的度（即直接相连的顶点数）
• 空间复杂度：，其中 是顶点数， 是边数。

邻接表的使用场景

• 适用于稀疏图，因为它们在存储上比邻接矩阵更节省空间
• 不能处理有反向的边的情况
• 在稀疏图中添加和查询边时更加高效，但牺牲了查询任意两个顶点之间是否存在边的时间复杂度（需要遍历链表）

邻接表的实现

建图

struct edge{int v,w}; //每一个点存储出边和边权
vector<edge> e[N];//每一个点
 
int main() {
  cin >> n >> m; 
  for(int i = 1 ; i<=m; i++) {
    cin >> a >> b >> c;
    e[a].push_back({b,c});
    e[b].push_back({a,c}); 
  }
  dfs(1,0)//从根节点开始搜索,根节点没有父节点
}

遍历

遍历分为两种，一种是dfs遍历，一种是bfs遍历
DFS遍历

void dfs(int u, int fa) { //fa是起点的父节点
  for(auto ed : e[u]) { //遍历每一个点
    int v = ed.v, w = ed.w;
    if(v==fa) continue; //因为被正反存过两遍，所以当前的出边是遍历过的父节点，不再搜索
    cout << u << v << w;
    dfs(v,u)//当前节点是父节点，进入子节点搜索
  }
}

BFS遍历

void bfs(int u) { //从根节点开始搜索
  queue<int> q; //定义一个队列
  q.push(u);//根节点入队
  while(q.size()) {//队列不为空
    int x = q.front();//取出队首元素
    q.pop();//队首元素出队
    for(auto ed : e[x]) {//遍历每一个点
      int v = ed.v, w = ed.w;//取出每一个点的出边
      cout << x << v << w;//输出
      q.push(v);//子节点入队
    }
  }
}