邻接矩阵

05:21
用二维数组来存储边和权值，比如 表示，1去向2，之间的权重是20

设图的顶点数量为 ，「邻接矩阵 adjacency matrix」使用一个 大小的矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 或 表示两个顶点之间是否存在边，或者直接用这个值来定义权重

如下图所示，设邻接矩阵为 、顶点列表为 ，那么矩阵元素 表示顶点 到顶点 之间存在边，反之 表示两顶点之间无边。

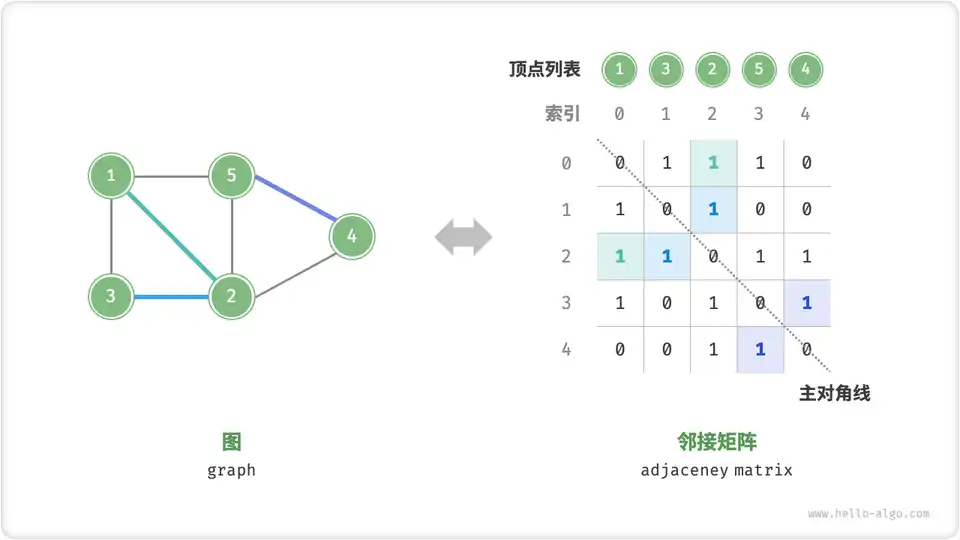
邻接矩阵具有以下特性。

• 顶点不能与自身相连，因此邻接矩阵主对角线元素没有意义。
• 对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称。
• 将邻接矩阵的元素从 和 替换为权重，则可表示有权图。

使用邻接矩阵表示图时，我们可以直接访问矩阵元素以获取边，因此增删查操作的效率很高，时间复杂度均为 。然而，矩阵的空间复杂度为 ，内存占用较多

邻接矩阵的复杂度

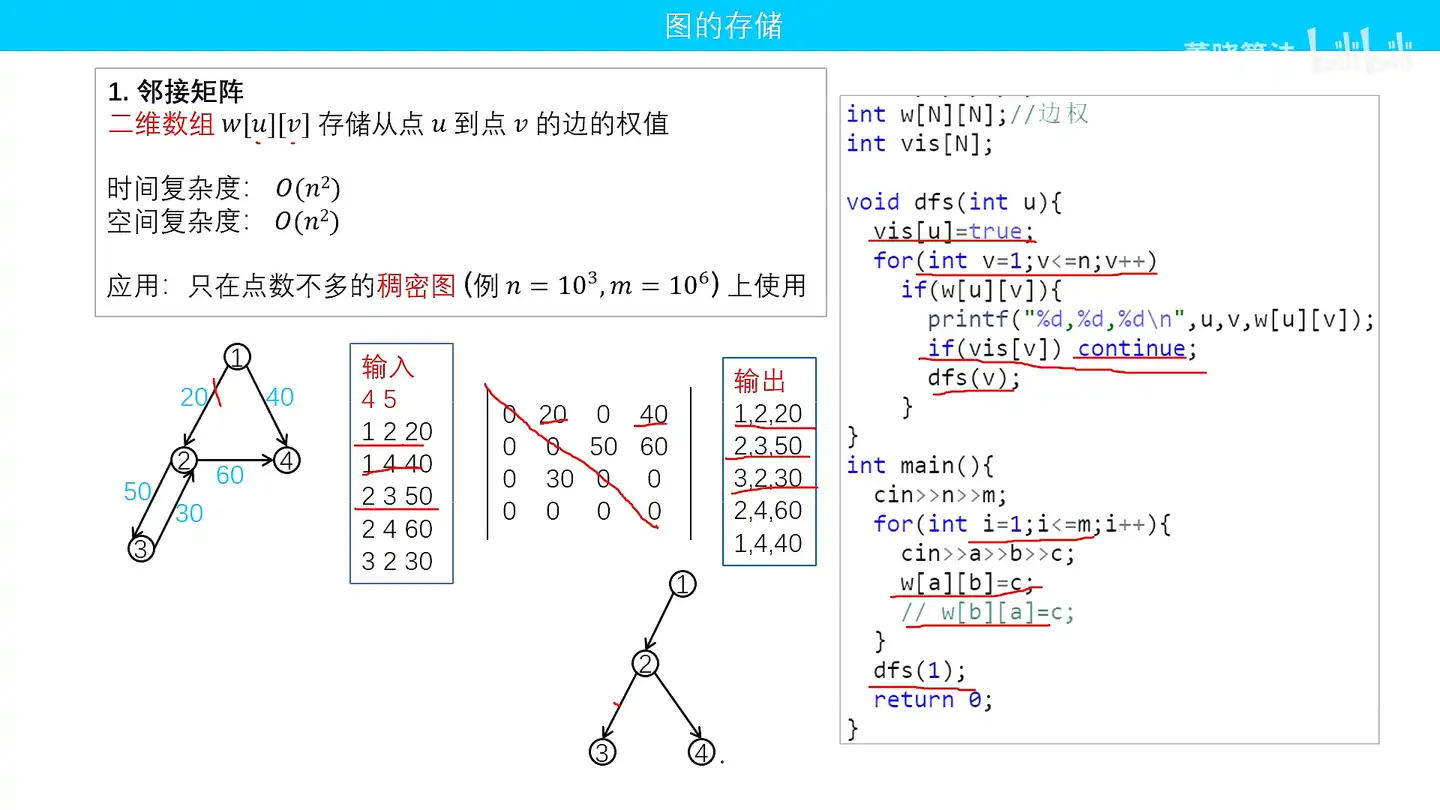
• 时间复杂度
• 空间复杂度

邻接矩阵的使用场景

点数不多的稠密图

邻接矩阵的实现

建图

int main() {
  cin >> n >> m;
  for(int i=1; i<=m; i++) {
   cin >> a >> b >> c; 
   w[a][b] = c; 
  }
  dfs(1); //遍历
}

遍历

void dfs(int u) { //从哪个节点开始搜索
  vis[u] = true; //这个节点来过
  for(int v = 1; v <= n; v++) { //v的相邻节点
    if(w[u][v]) { //这个节点是有值的，那么就是两点有联系
      cout << u << v << w[u][v];
      if(vis[v]) continue; //如果已经遍历过，1 2 20 和 2 1 20 是同一个东西，跳过
      dfs(v); //向下搜子节点 
    }
  } 
}