边集数组

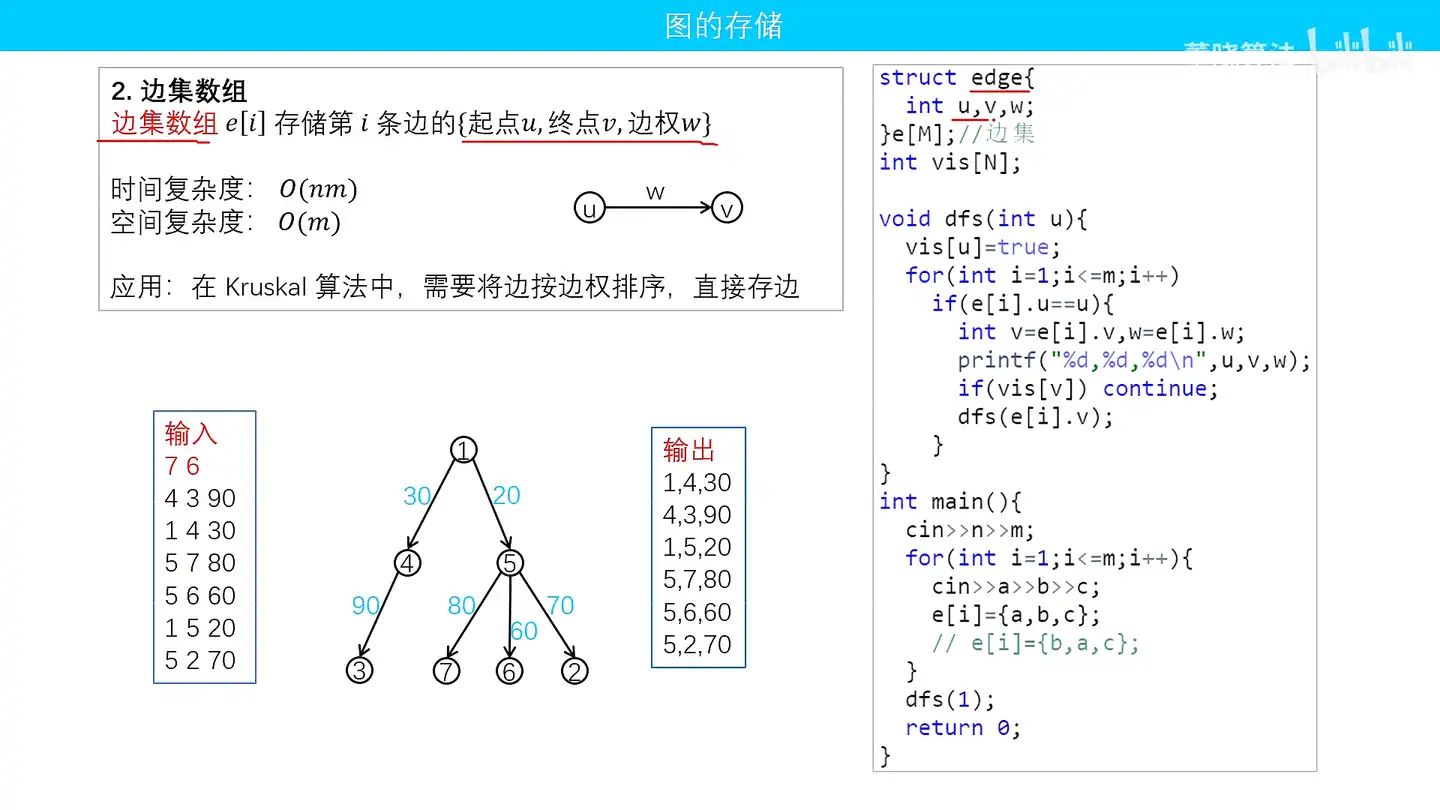
定义一个集合，这个的枚举来定义图中一个节点的三个元素

• 起点
• 终点
• 边权
  这个集合是边集数组 图中的每一个边由每一个 来组合出来

IMPORTANT

边集数组的 是图中的每一条边

边集数组的复杂度

• 时间复杂度：
• 空间复杂度：

边集数组的使用场景

需要将边按照边权来进行使用的时候，比如在kruskal算法里面，要按照边的权重为判断指标来做决策

边集数组的实现

建图

定义集合e

struct edge{
  int u,v,w;
}e[N];

int main() {
  cin >> n >> m;
  for(int i = 1; i<=m; i++) {
    cin >> a >> b >> c; //a是起点，b是终点，c是边权
    e[i] = {a,b,c};
  }
  dfs(1) //自己决定起点
}

遍历

void dfs(int u) { //起点编号1
  vis[u] = true; //来过了1
  for(int i = 1; i<=m; i++) {
    if(e[i].u==u){//第1条边的起点，是不是点1，如果不是，找到起点是1是这个边，操作这个边
      int v=e[i].v, w=e[i].w; //取出这条边的权重和终点
      cout << u << v << w; //当前的点线关系
      //如果这个边的终点，已经去过了
      if(vis[v]) continue; //我们就不去了
      dfs(e[i].v) //否则我们去到终点为起点的边
    } 
  }
}