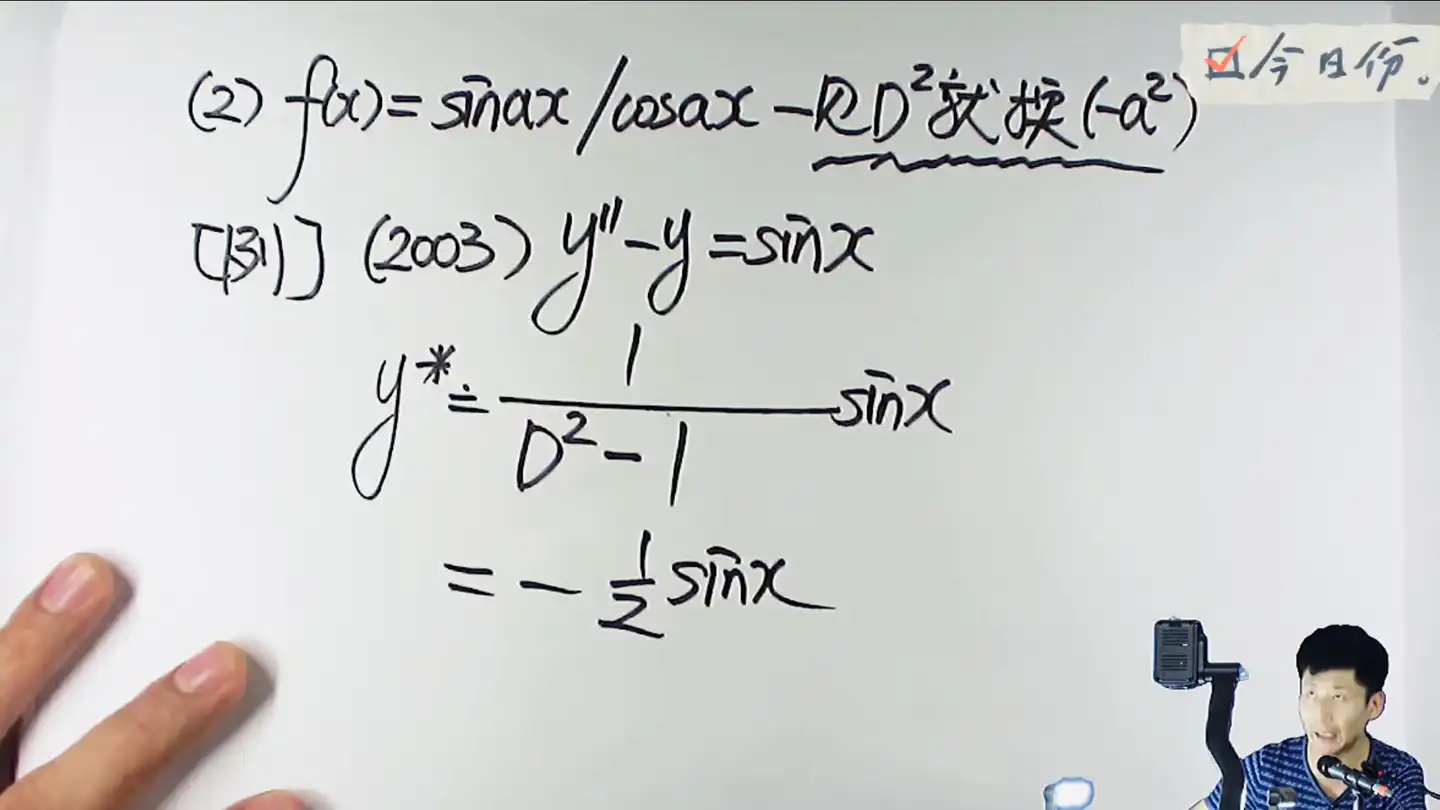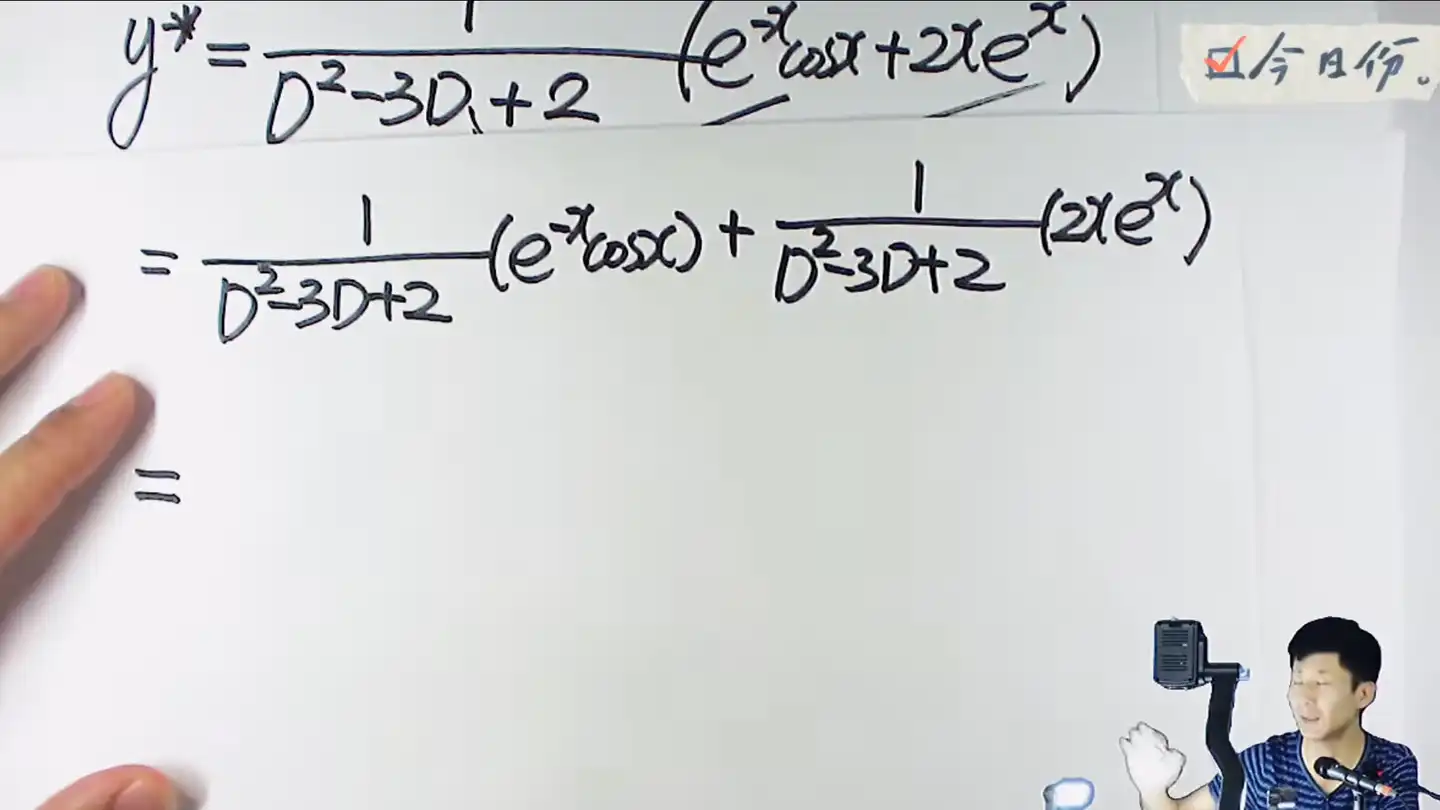自由项是e,见D就换k
自由项
例题
特解
特征方程用算子描述
此处
练习

解答
练习
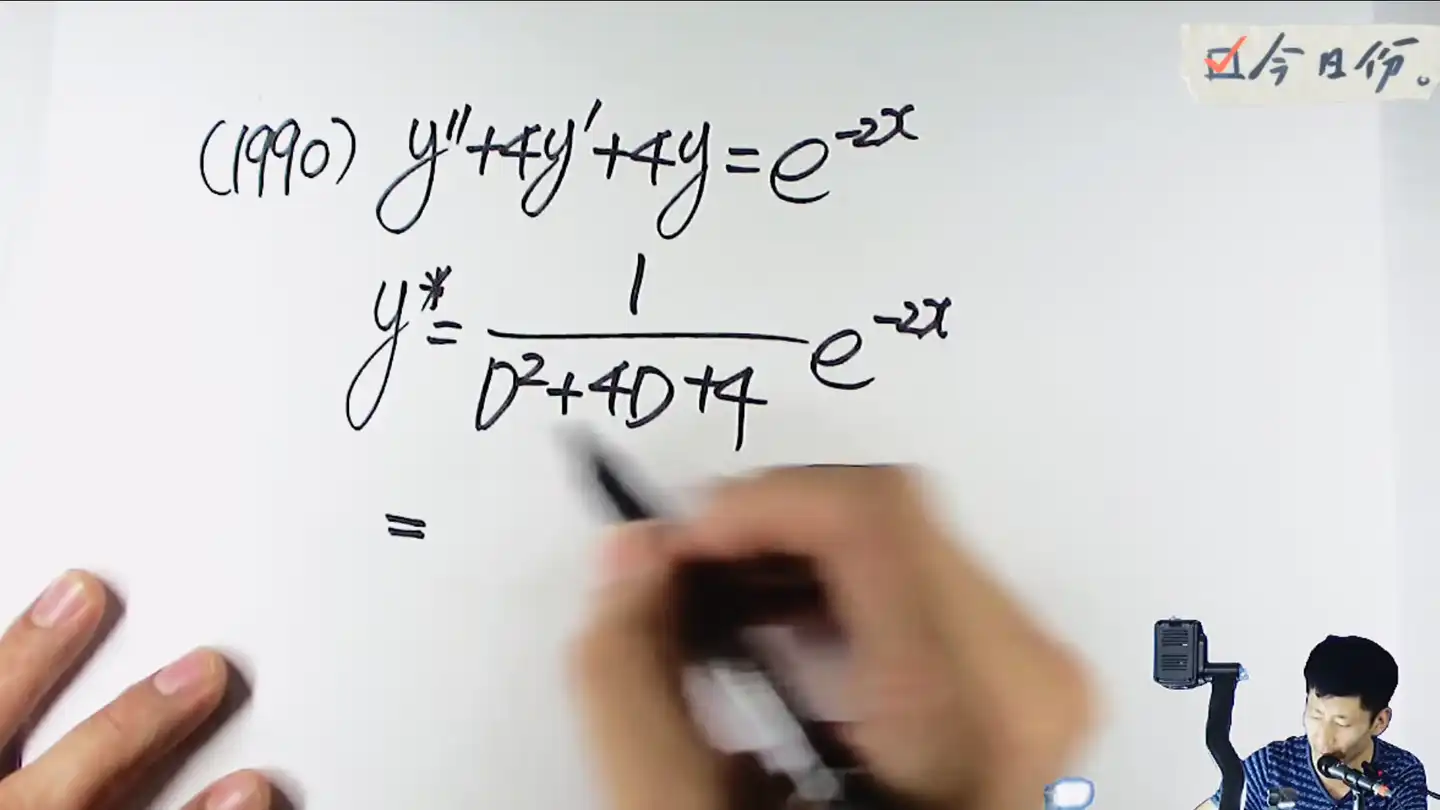
分母为零如何处理
- 00:12:33
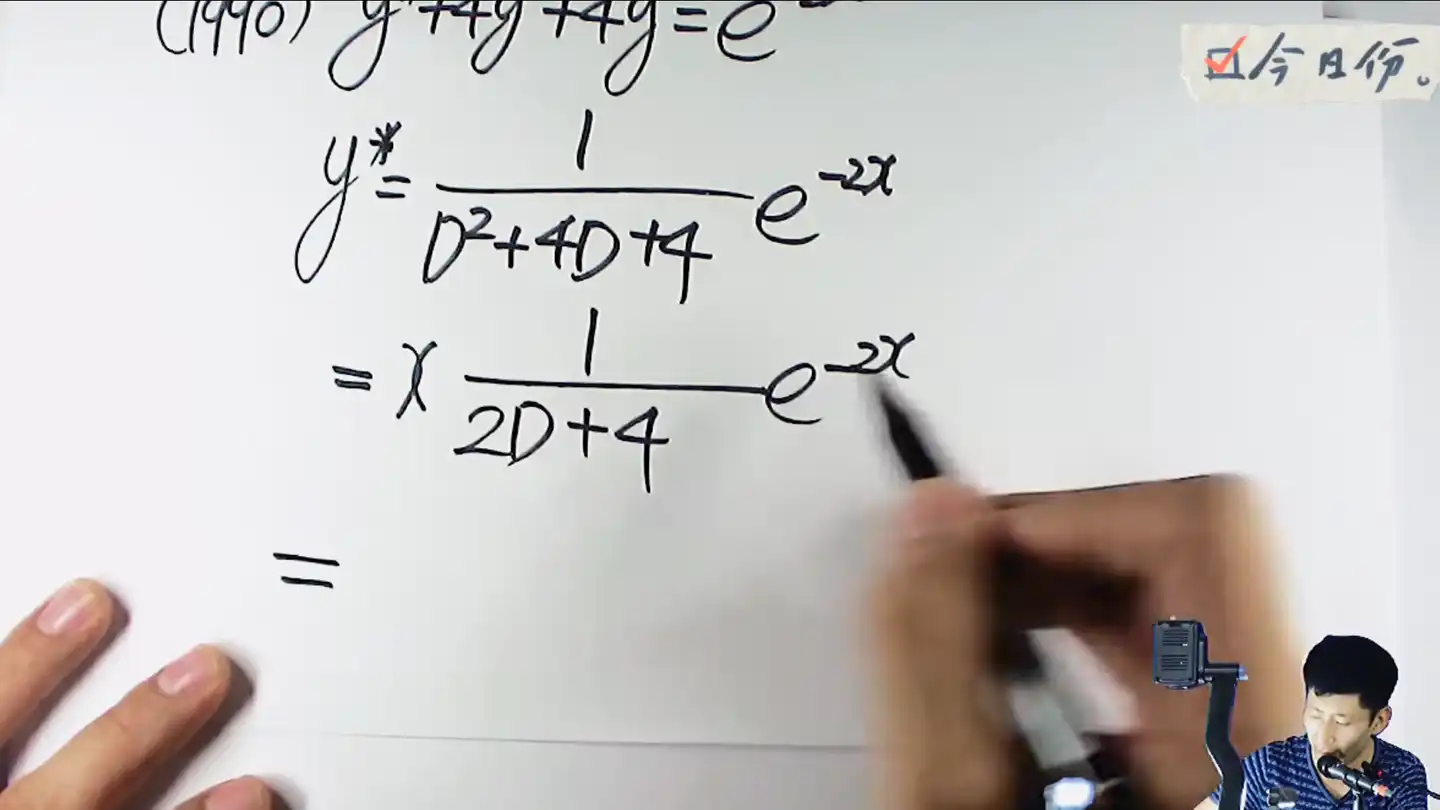
提一个x出来,对着特征方程求导
这里带进去,分母还是为0,继续提一个x出来,然后对着特征方程求导
自由项是三角,见D方就换-a方
自由项
注意这里的a
例题
特解
代成算子
把
练习
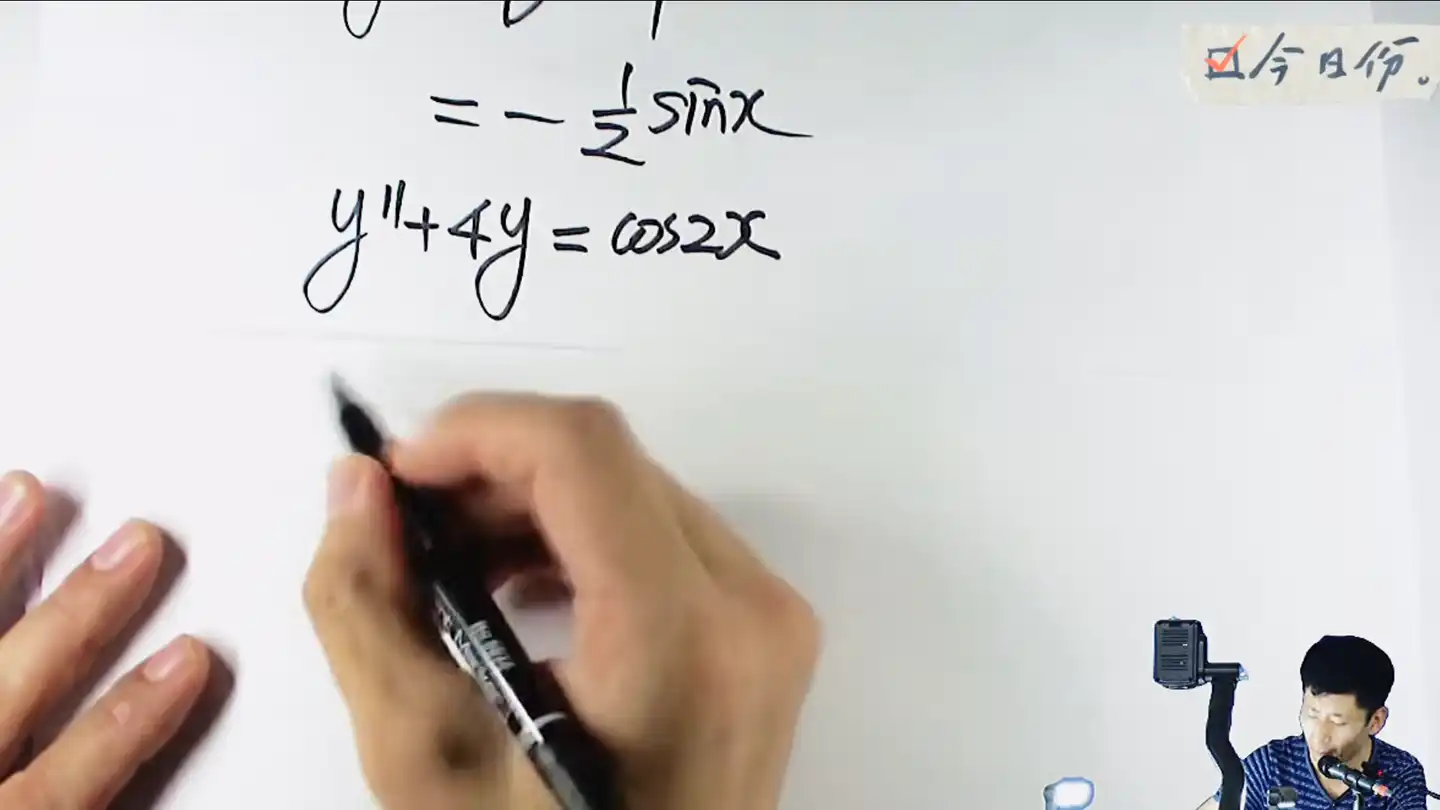
分母为0提x,导一次
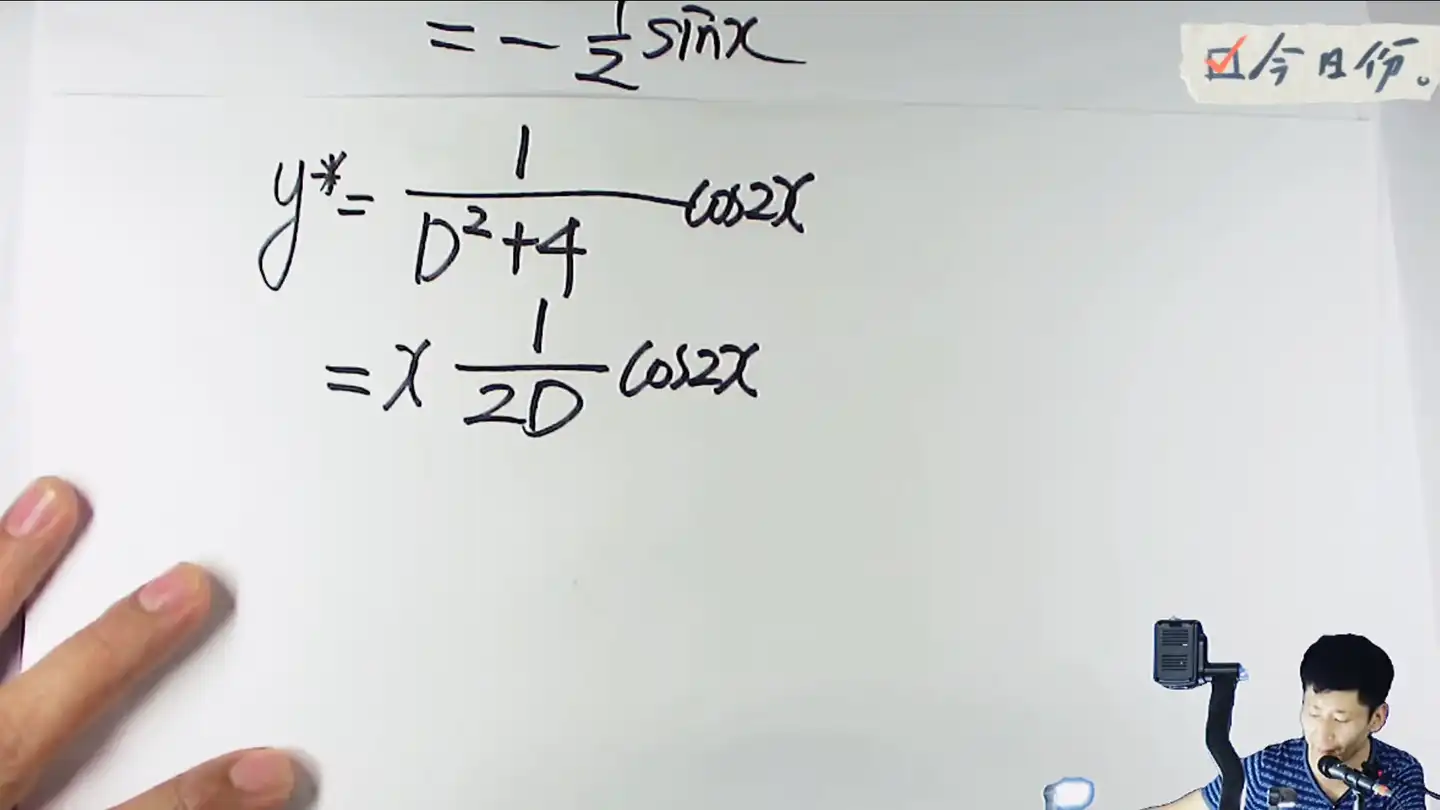
这里得到
其中
abc系数全齐
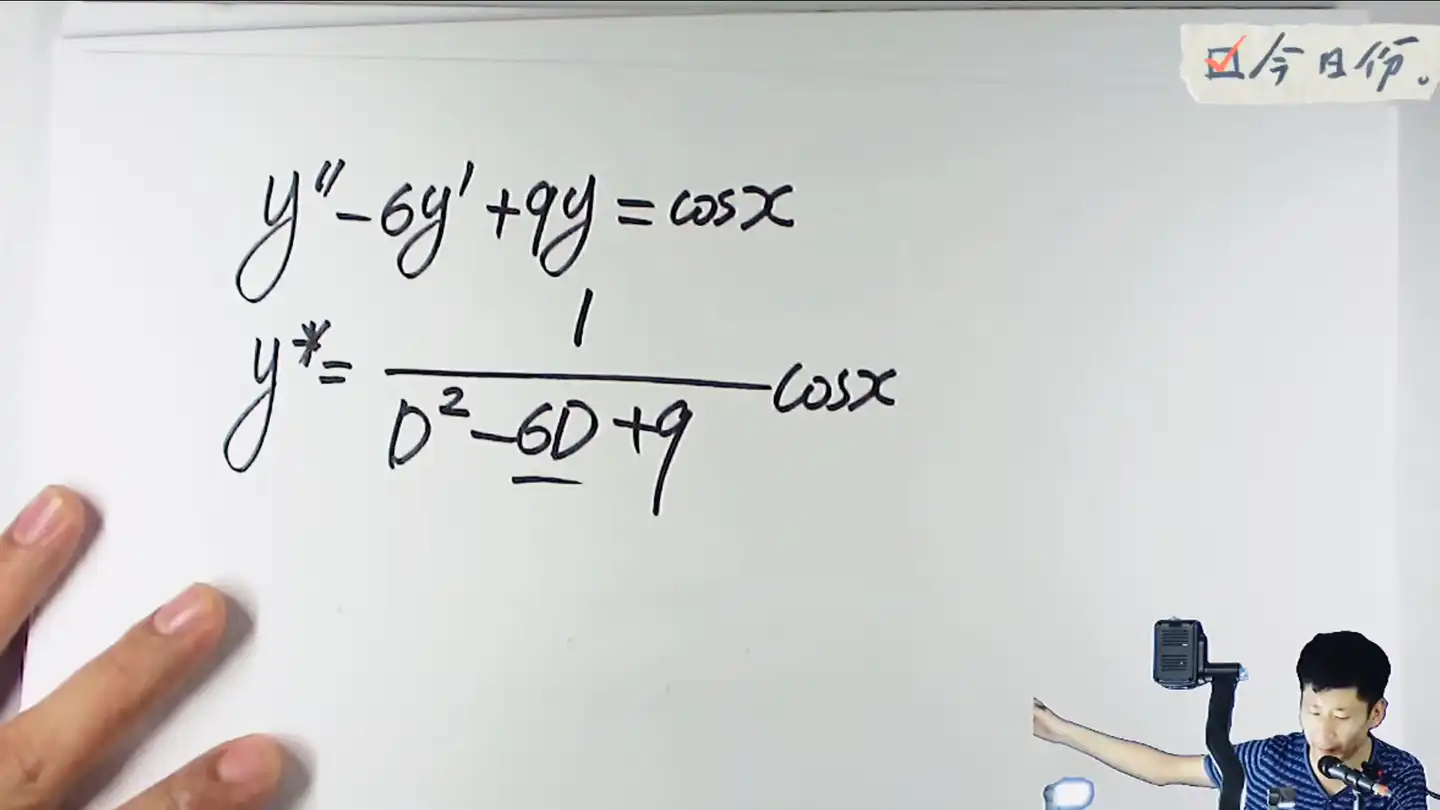
依然先转化为
接着根据见D方换-a方的原则换掉D方 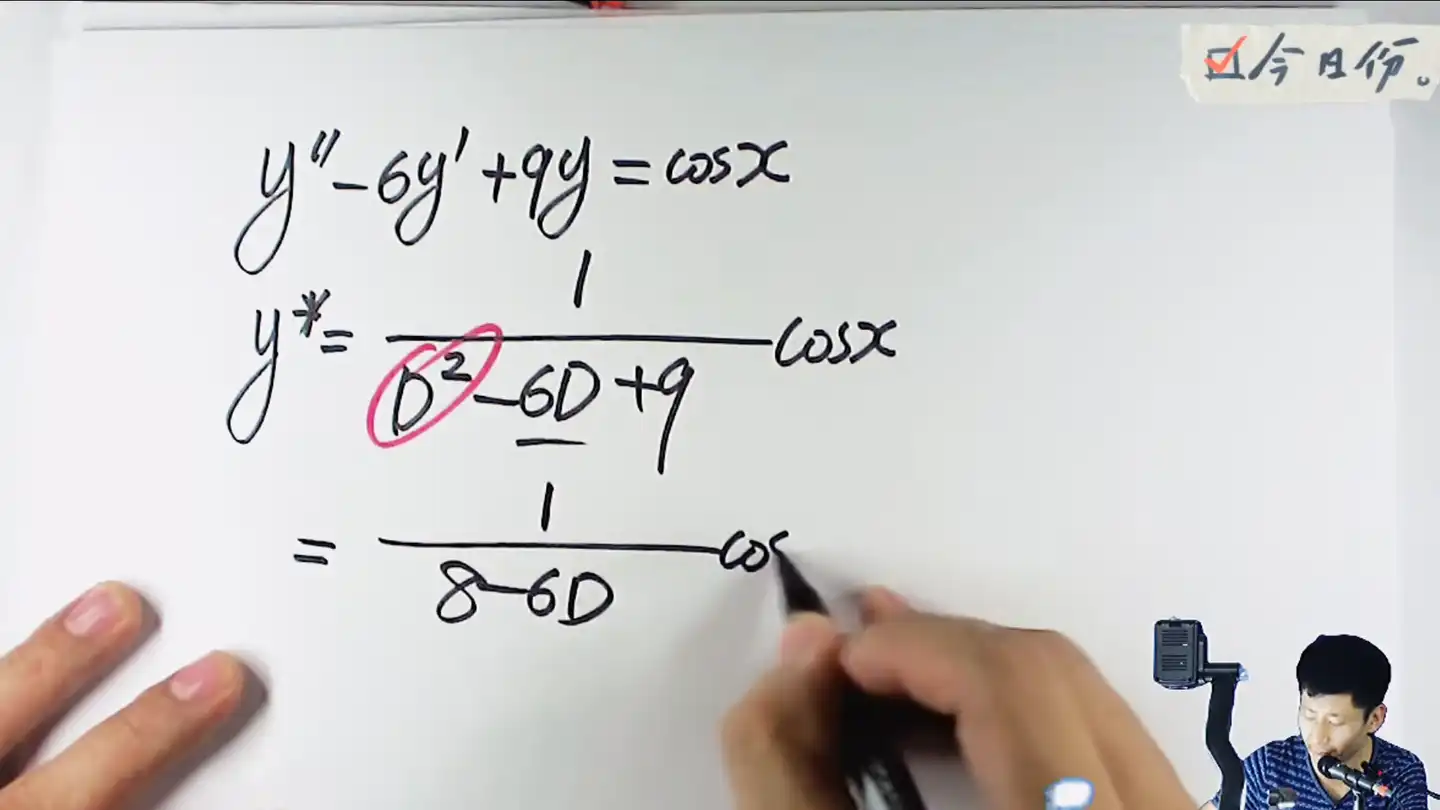
没有方了,接着平方差公式凑平方 
继续用见D方换-a方的原则换掉D方 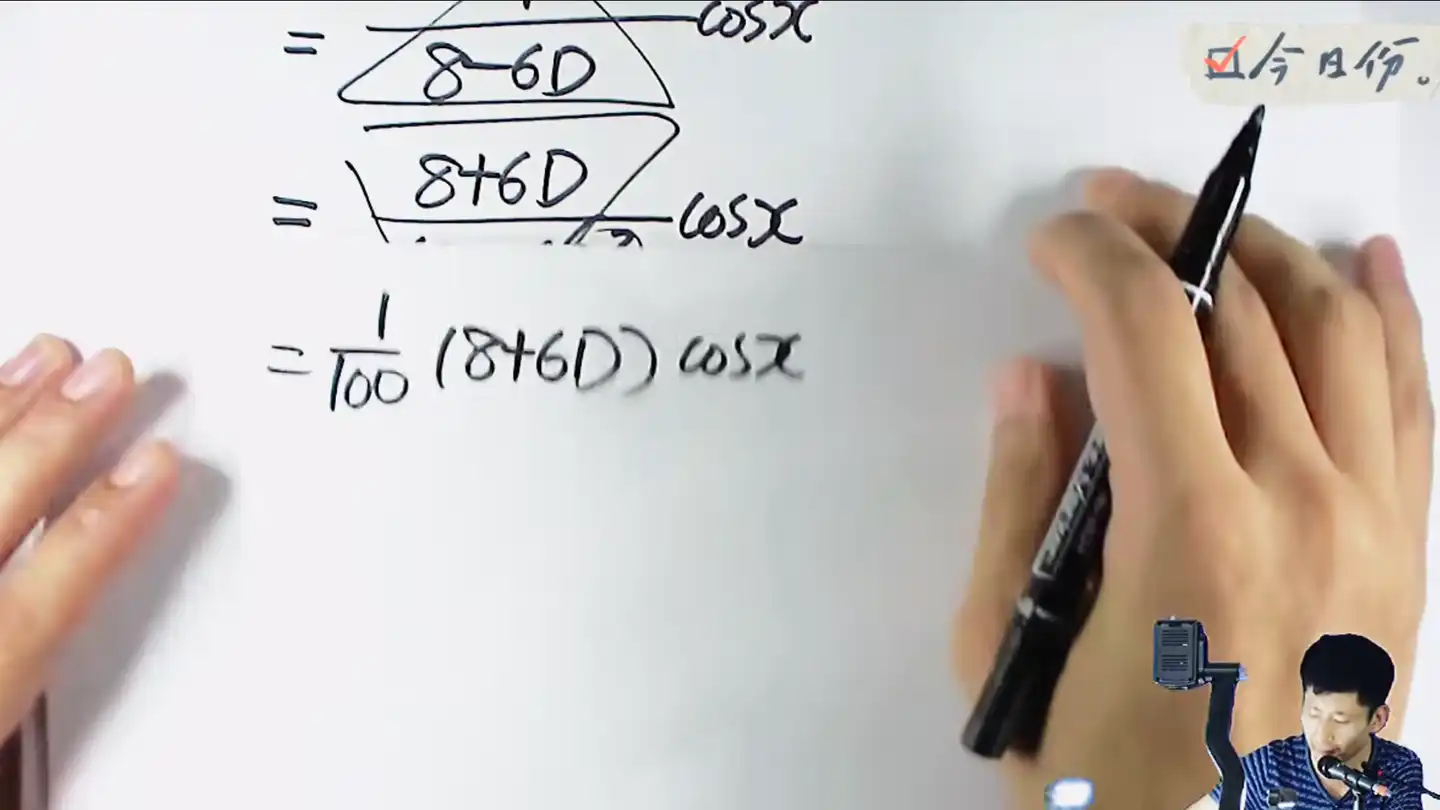
接着把算子D和自由项放在一起进行求导 
自由项是x的多项式
有一些前置的细节,需要了解 - 00:21:33
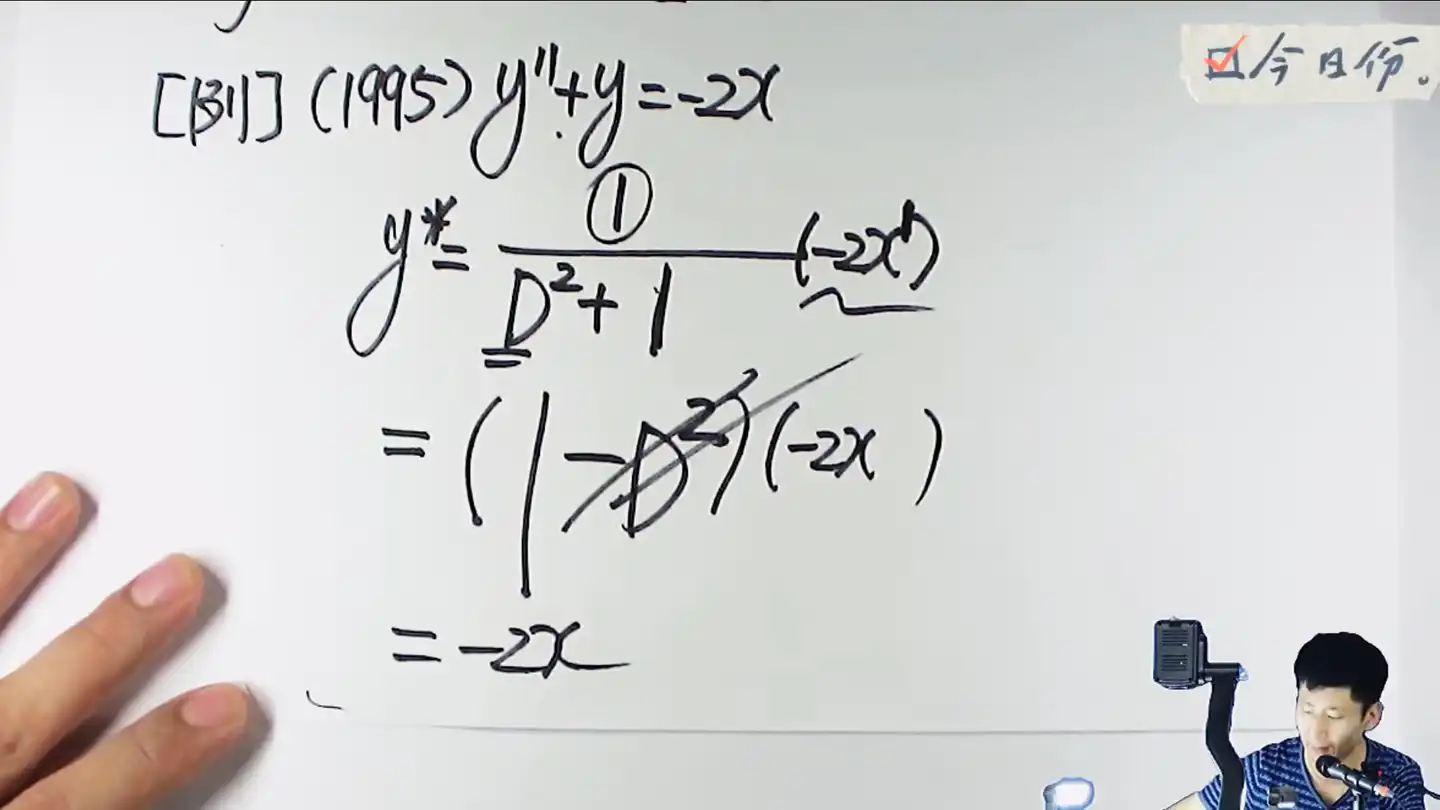
和之前的套路一样,先写出来这个固定的
然后需要把特征方程这部分用无穷递缩等比公式来改写一下,这里的D存在一个展开的项数的问题,这个展开多少和自由项的次数相关,比如在图中这个示范中,自由项是1次的,甚至都不需要D,因为这个D是二次的,已经超过了这个1次,是展不开到这里的
练习
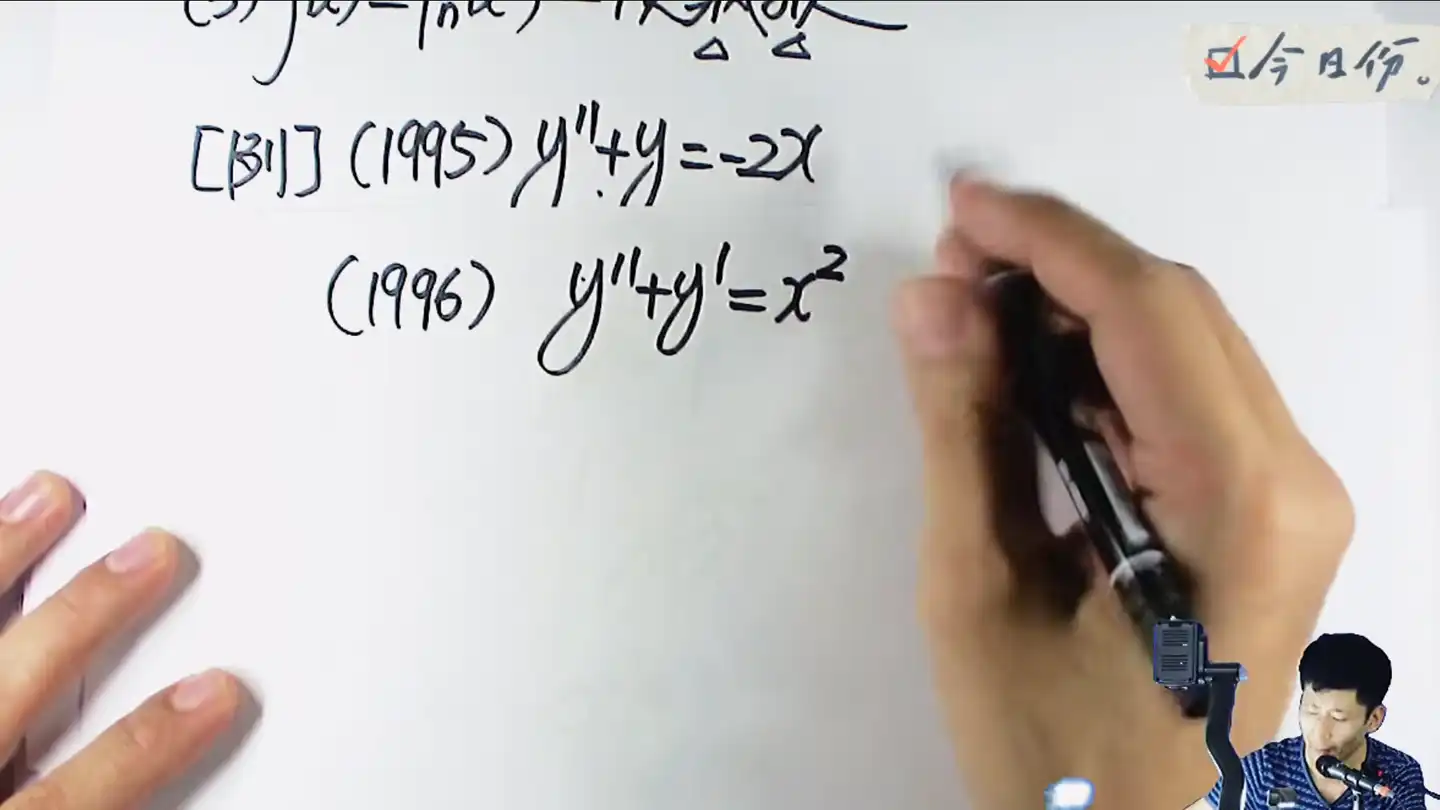
自由项2次同时系数有ab
依然先按照套路写出来这个先
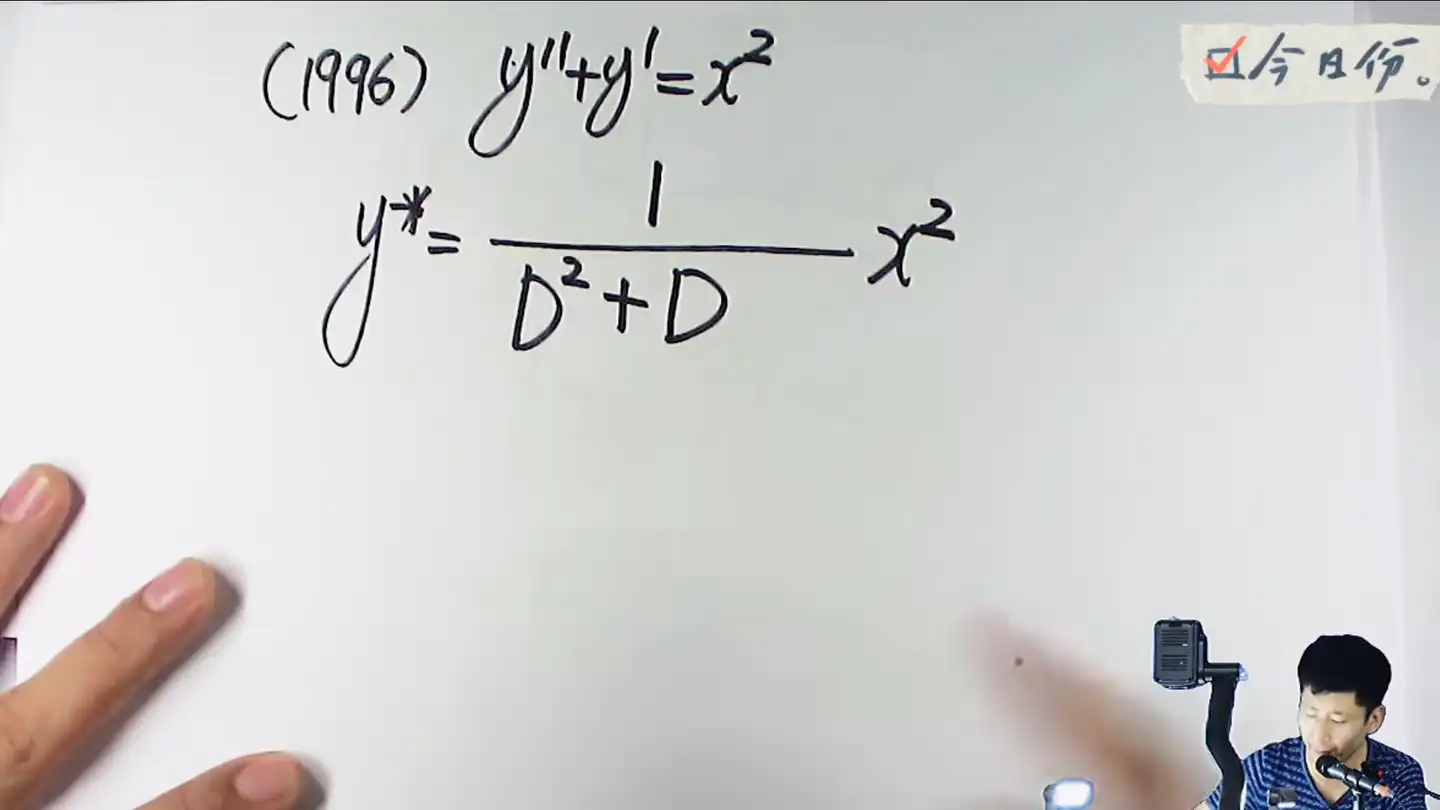
这里得到的式子里面没有
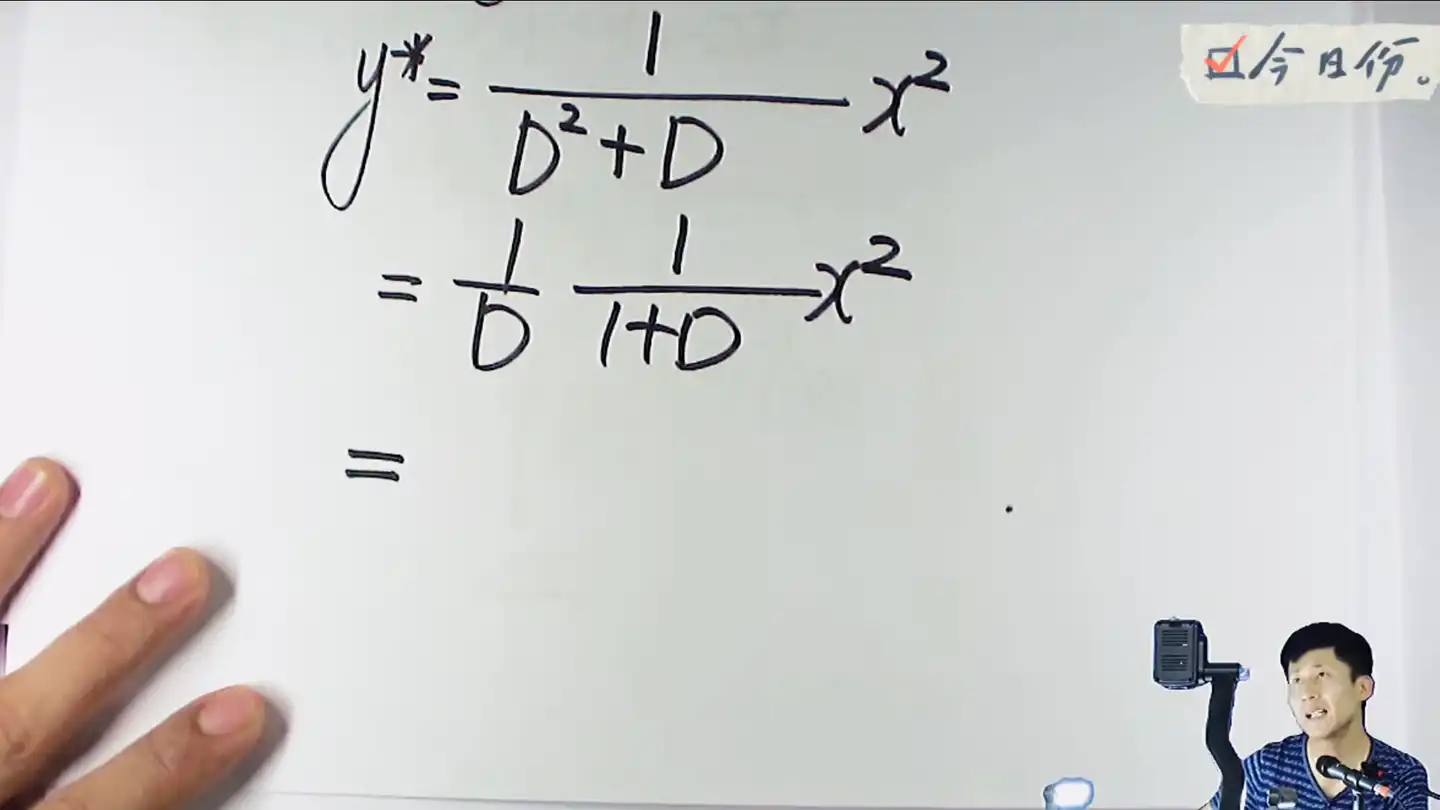
提出来以后,这里式子的优先顺序是从右向左匹配,这里的 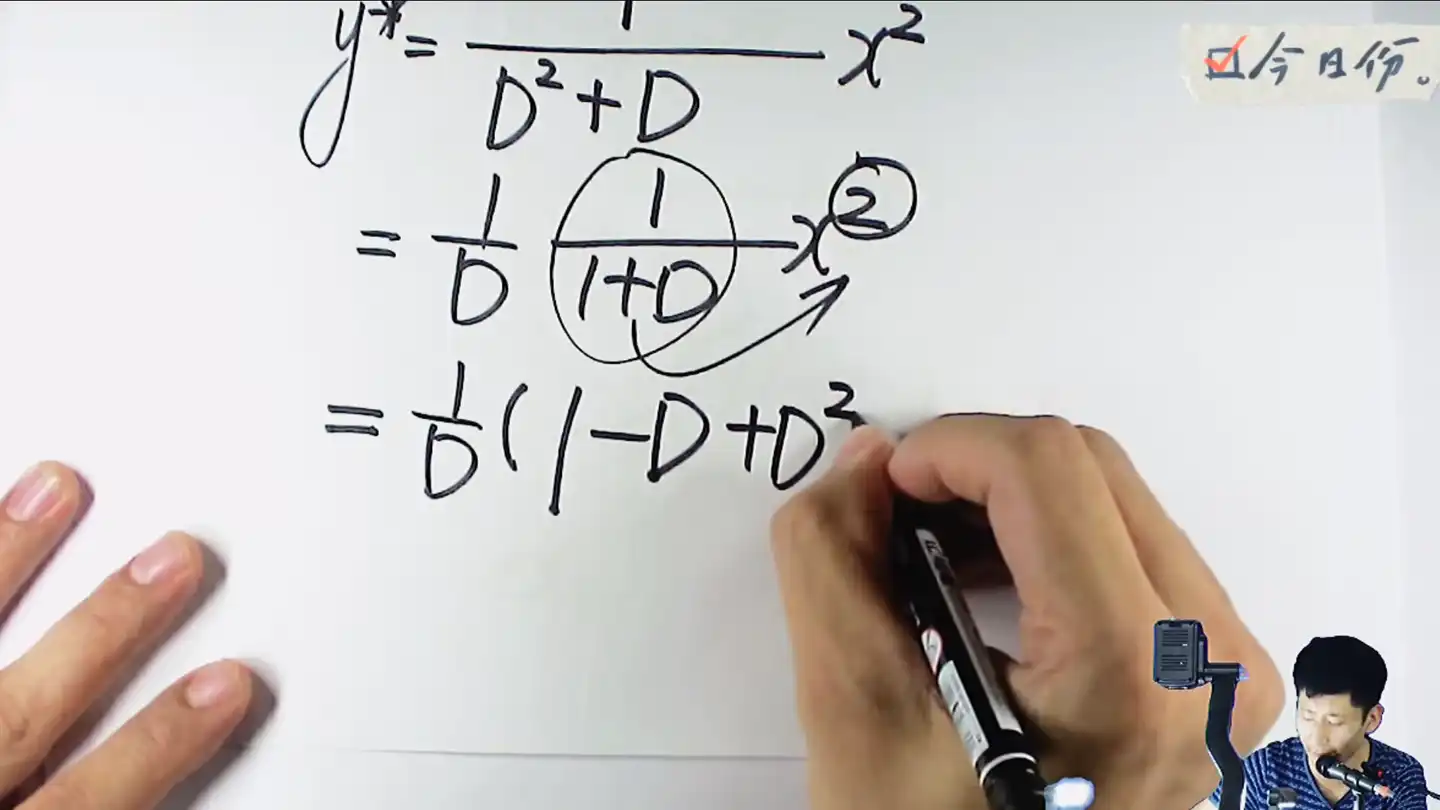
第二项这里是负数,第三项就写正数,还要带着次数升幂,因为自由项最高是2次的,这里展开还原的数列写到2次就差不多了 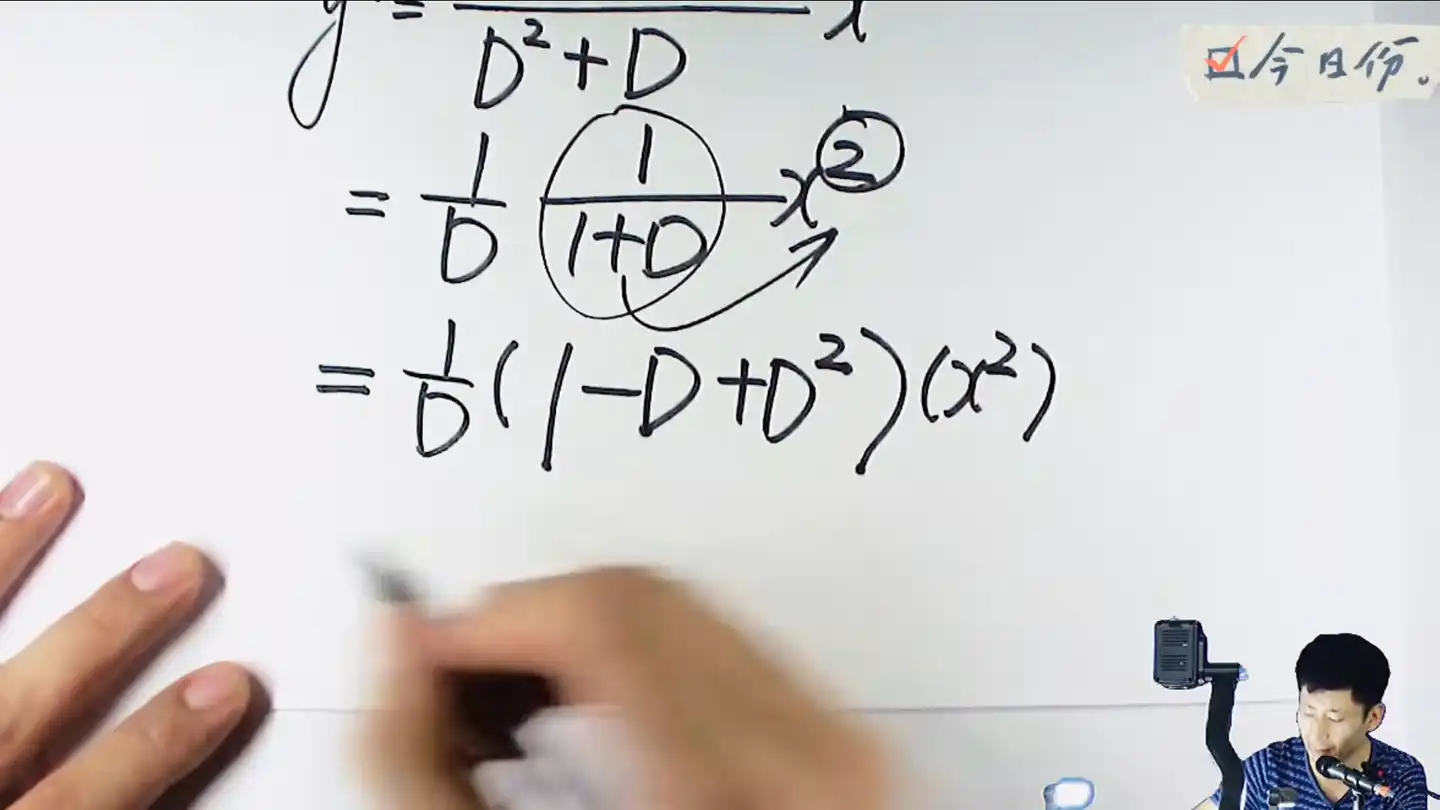
接着还是近水楼台先得月,从右边往左边走,根据运算法则对x进行作用,D是求导,D方是二阶导,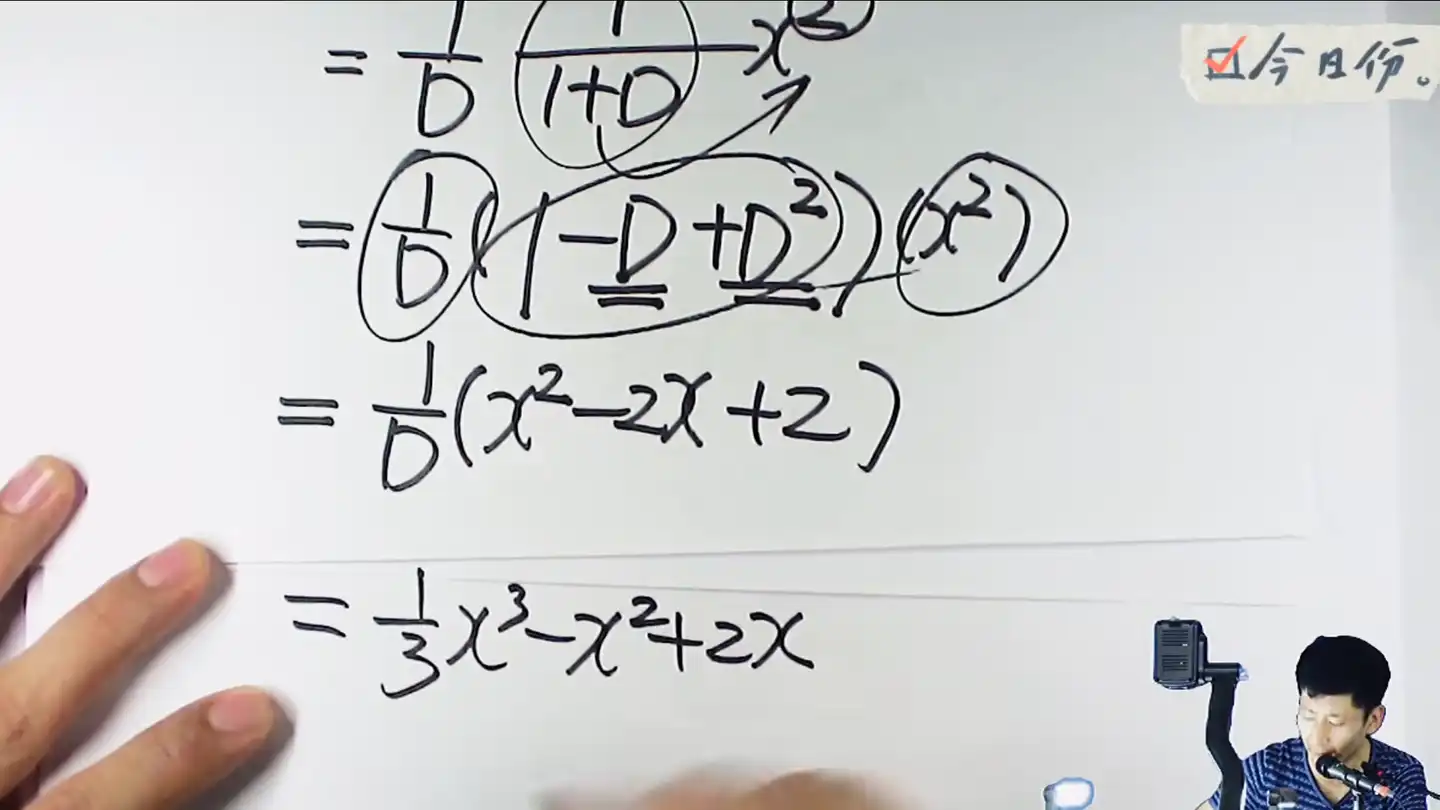
- 00:26:36
如果自由项这里写成这种的,上面这个时间戳这里说明了,可以正常带着常数 
abc加二次自由项全齐
这还是之前多项式自由项这种,只是这里是abc系数全齐全,比较复杂
还是秉持这几个原则
- 近水楼台先得月
- 凑出来
- 把分式展开还原成多次幂的数列排列
比如说下面这里拿到这个,可以提取出来一个2,把常数这里凑配为1,然后按照来处理 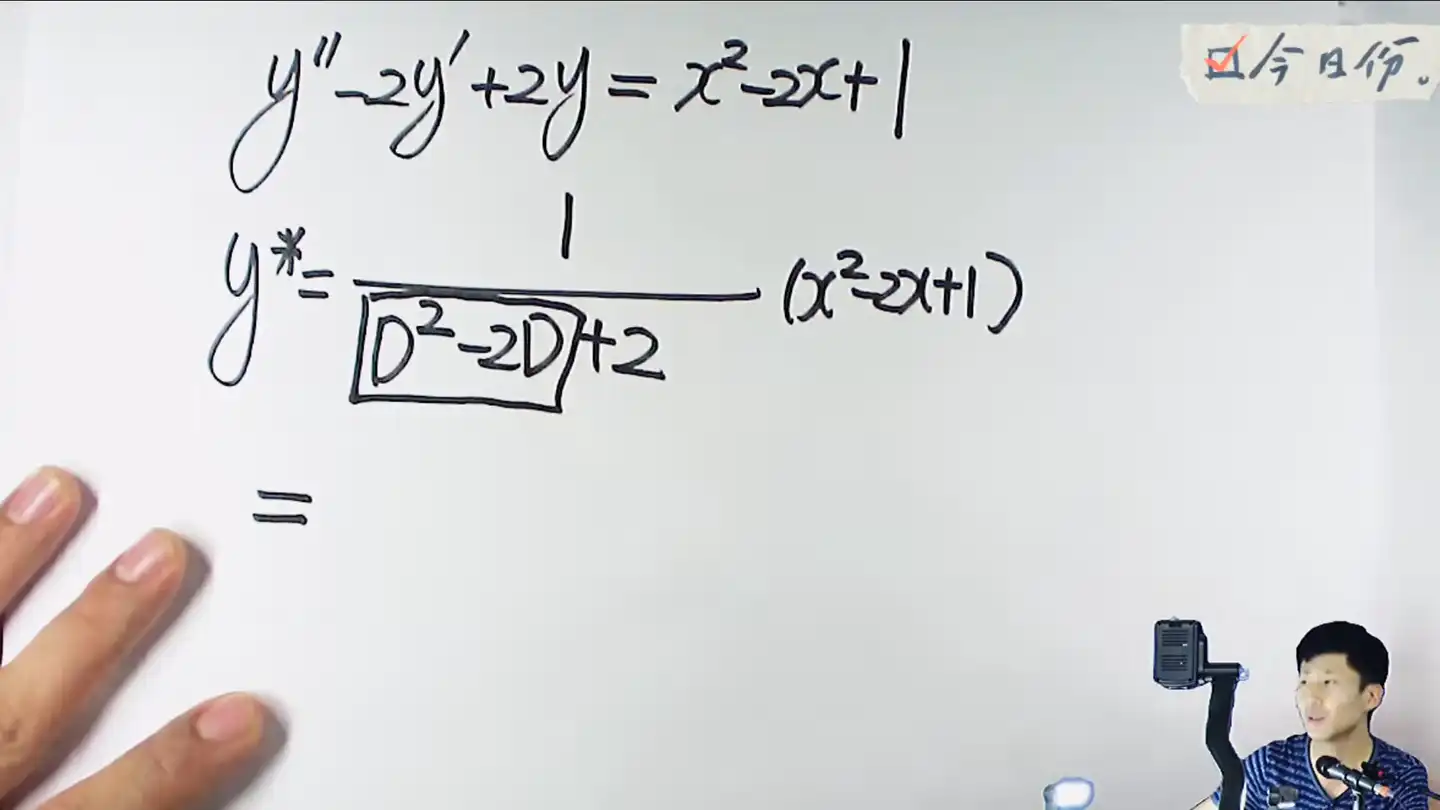
但是可以有一些简化的计算手段,这里进行一些说明 - 00:28:58
根据下面这个式子来做一个说明
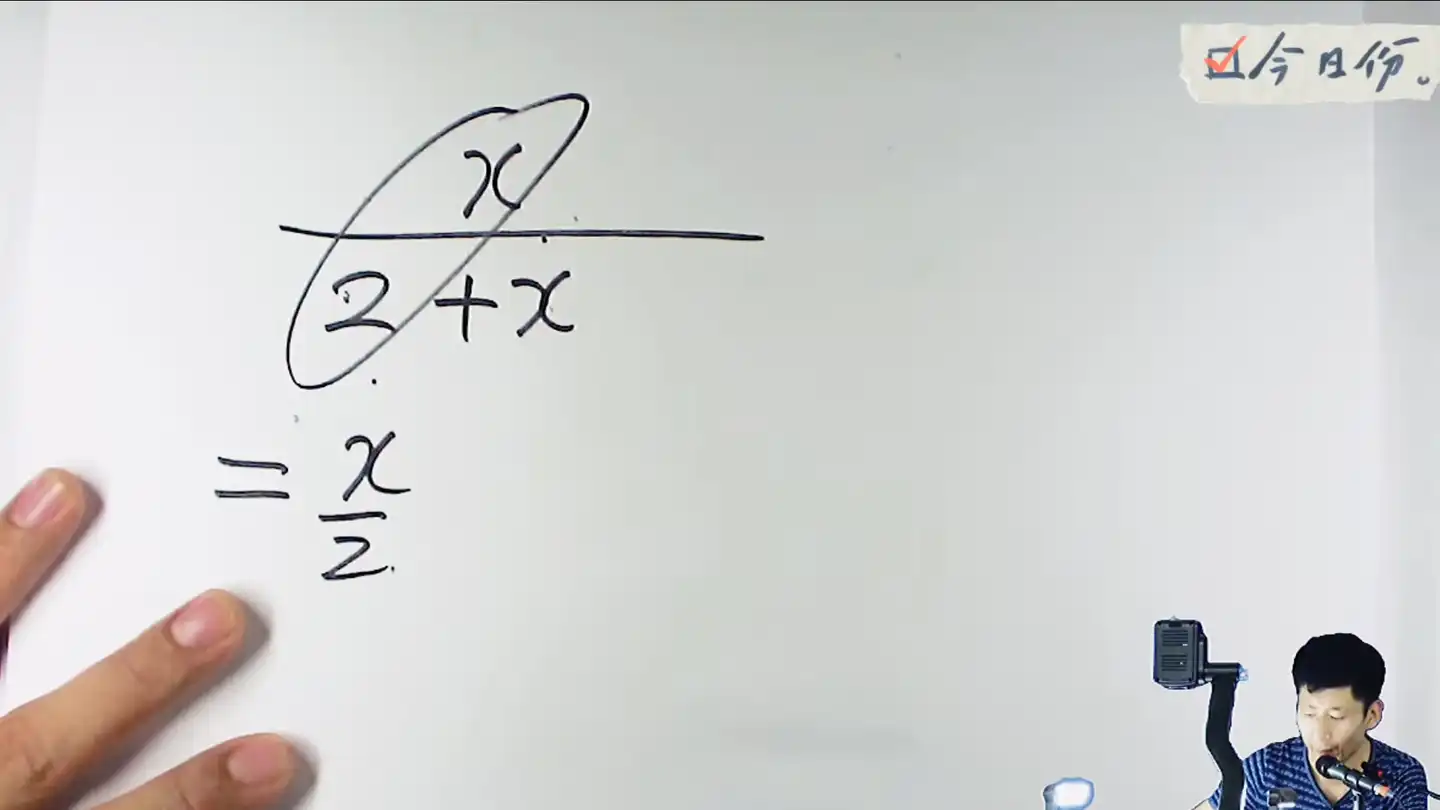
把这个视作等比的求和式子,还原成数列的幂次 - 首项
- 分子的a,这里是x来除以,分母上的常数也就是首项是
- 分子的a,这里是x来除以,分母上的常数也就是首项是
- 公比
- 用这里的一次项,来除以2,也就是
,公比带上负号
- 用这里的一次项,来除以2,也就是
- 依次乘上公比,还原展开成数列幂乘

也就是说,都是把东西拿出来除以这个常数,注意,这里举例的部分,只是恰好这两个部分都是x了,分别是代表的不同的字母,首项a和公比q
对例题示范的解答

这里需要把左边除开常数的部分视作是一个整个,也就是方框框起来的部分,这一团视作公比,2这个常数视作为等比数列求和的那个1的部分
- 首项
- 这里的第一项
是 得来的
- 这里的第一项
- 公比
- 方框除以2,带上负号就是这个公比
- 最高次为2
- 公比要乘2次,写到公比的2次停
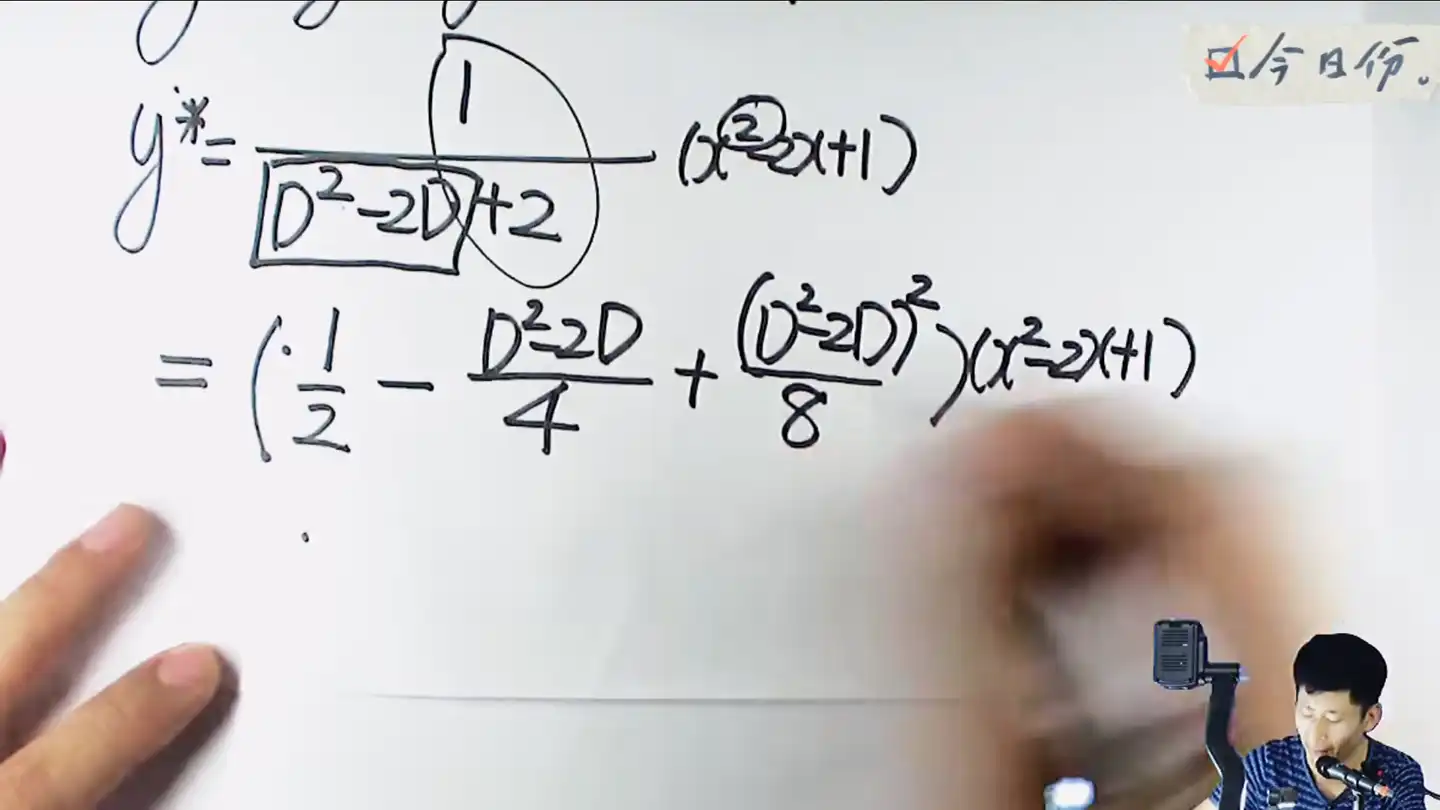
然后处理一下左边这一团式子,展开式子,只留下二次和二次以下,三次和四次的部分都丢掉,得到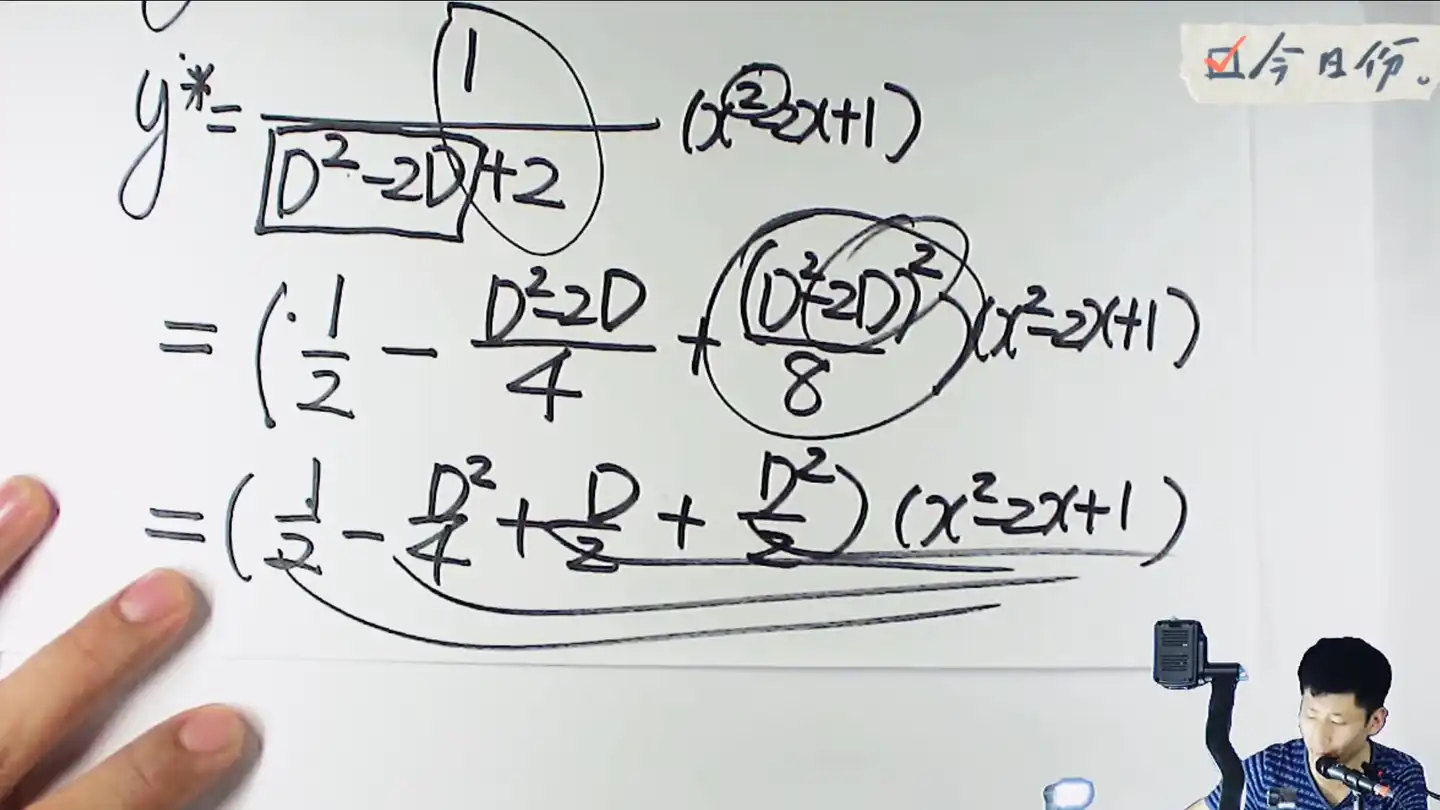
- 公比要乘2次,写到公比的2次停
自由项是e配y(x)
形如:
给这个算子的函数的自变量加一个偏移量k得到
解
自由项是xsinx类-多项式乘三角,没考过
原理说明: - 00:45:33
示范:- 00:47:10
综合练习
习题1
注意,这里解的叠加原理,可以分开算再合起来