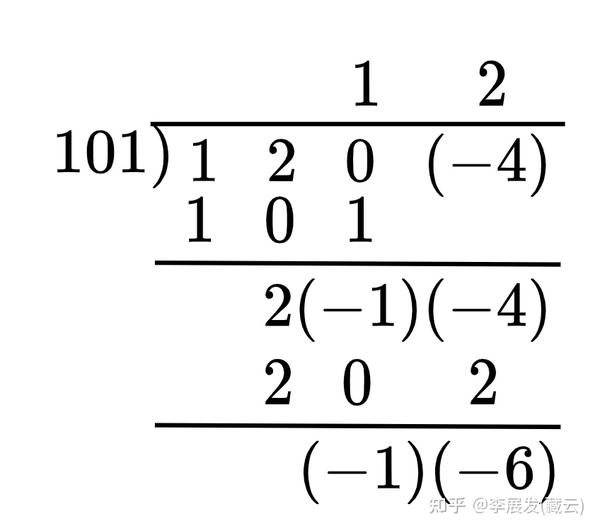第一步：分离出真分式

在上式中，当最高次幂小于中最高次幂，我们称为一个真分式。例如：

最高次幂是1，最高次幂是2，因此它是一个真分式。

我们可以类比，分子小于分母的分数，被称为真分数。例如，就是一个真分数，而是一个假分数。

正如我们可以把一个假分数简化成一个整数加上一个真分数：

方法是用除以得到，余。

同理，当不是一个真分式，也可以通过分式除法化简成一个多项式加上一个真分式的形式：

多 项 式 真 分 式

注：

对于学习过进制的同学，可以更好地理解这一点。如果我们站在10进制的角度来看，123其实是一个十进制的“多项式”:

因此，我们可以把

这个多项式看成一个进制的数。因此，除法和分式除法并没有本质的区别。只是一个是10进制下的，一个是进制下的。

现在，我们看看如何把一个假分式化简成一个多项式加上一个真分式的形式。

我们小学中学到的除法式是这样的：

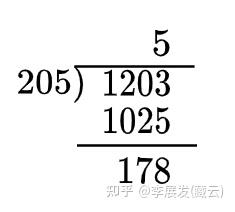
分式除法跟这个是一样的。设求解的分式如下：

首先，两个式子中的项按的幂进行排列，并且补足缺失的的整数幂的项：

用分式除法写下来：

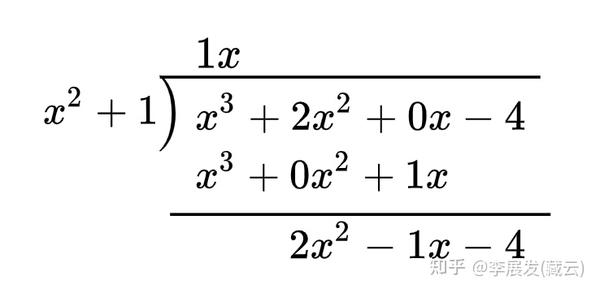
再继续除：

长除法的结果应该怎么放位置

余数是除不够的，自然就是分子
整除的结果自然就是在上面
左边是分母

因此：

如果你对这种方法很熟悉，或者能够理解前面“注”中进制的角度，你可以直接像小学除法式那样除，我们把全部扔掉，只拿出系数来处理。只是要注意一个区别，那就是系数在这里可以是一个负数，因此在做相减时，不进行借位：

YiNotes