第二种分式
对于分母为
同样,分子应当是一个常数。因为如果分子包含有
现在,我们说一个真分式:
它可以进一步化简为以下几个分式之和:
因为它是一个真分式,所以
无论
我们也可以使用“进制”的思想来理解这一点。不感兴趣的可以不看。
首先,一个有理真分数大于0小于1,即:

先拿

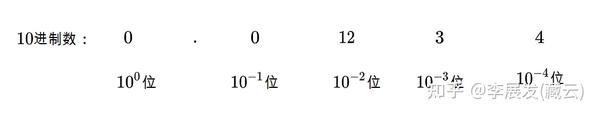

因为这个真分数小于1,因此必然
我们把这个步骤重复在
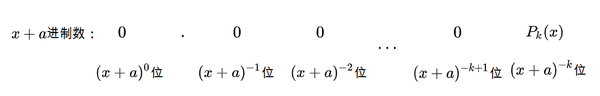
我们使
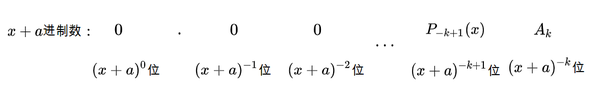
重复这个过程,如果
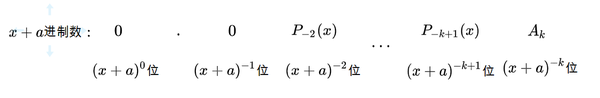
这个过程最多可以再进行一步,并停止在
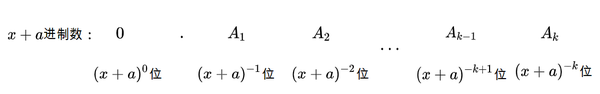
表示为十进制即:
Jun 19, 20253 min read
对于分母为
同样,分子应当是一个常数。因为如果分子包含有
现在,我们说一个真分式:
它可以进一步化简为以下几个分式之和:
因为它是一个真分式,所以
无论
我们也可以使用“进制”的思想来理解这一点。不感兴趣的可以不看。
首先,一个有理真分数大于0小于1,即:

先拿

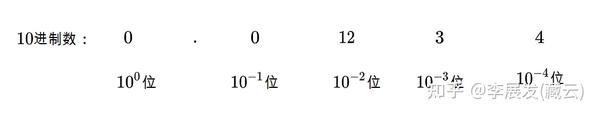

因为这个真分数小于1,因此必然
我们把这个步骤重复在
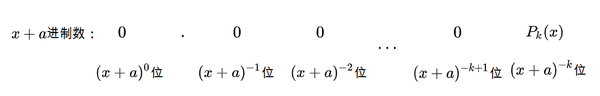
我们使
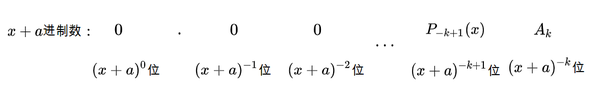
重复这个过程,如果
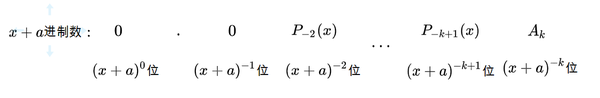
这个过程最多可以再进行一步,并停止在
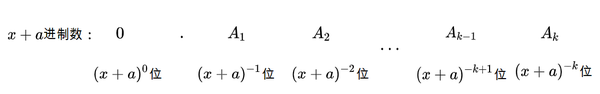
表示为十进制即: