求解这个方程,就是把它的系数矩阵通过初等变换转化行阶梯形矩阵
Q:如何理解列满秩和线性无关?
A:m行n列,m个方程n个未知数
齐次非齐次都是看的列数,列数就是变量个数,因为是解方程,所以我们始终关注变量x,也就是列满秩
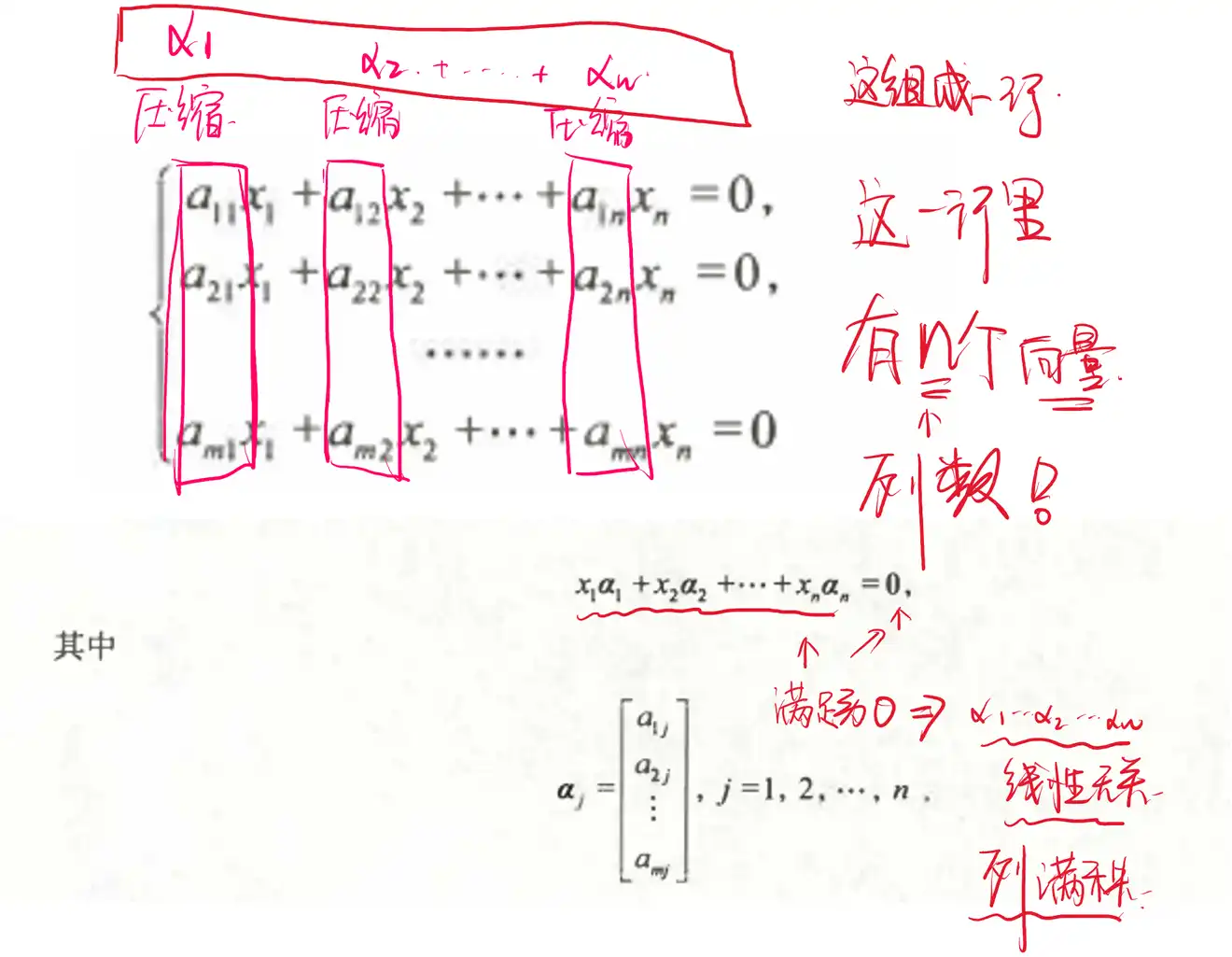
如果这里m和n是相等的,那么可以引入行列式来做判定,行列式为说明存在压缩,说明线性相关,说明变量比方程多,说明齐次有非0解
有解的条件
这个部分和线性相关的判定结合起来对比着看
当系数矩阵的秩为n时(n个未知数),说明对空间没有压缩,此时作用在一个n维向量上,得到的是0向量,说明;;方程组有唯一0解,这个变换矩阵只能是作用在0上,才能得到结果是0
否则就会把有的空间压缩到0空间,而这个空间上的所有向量经过A变换后都是0,也就是无穷多解
当系数矩阵不是满秩的时候,方程组有非零解(无穷多解),每一个有用的方程是一个约束,约束可以相互线性表示的向量,而余下的向量张成一个空间,这个空间里面那些受约束的向量,可以被余下的向量线性表示出来,这些向量有
这个S是就是这个方程组的解空间,一旦S的解空间确定了,那么

解的性质
这个系数矩阵作用在不同的解向量上会得到0向量,那么它们的线性组合还是解向量,也即是还是0,这都是同解方程组
解的结构
有解的条件中,提到的这n-r个不受约束的线性无关的向量,被称之为基础解系
Transclude of 二、齐次线性方程组#3-基础解系和解的结构
Q:如何理解矩阵的秩与解的个数关系: 对于 A,设其秩为
A:如果 Ax = 0 只有零解。
如果 Ax = 0 有无穷多解,其基础解系包含