初等矩阵

对单位矩阵 做一次初等变换，得到的矩阵称之为，初等矩阵

矩阵是一种对空间中元素的变换手段，初等矩阵就是这些具体的基础的简单的变换手段的数学表达形式

(1)一个非零常数乘矩阵的某一行(列);
(2)互换矩阵中某两行(列)的位置;
(3)将矩阵的某一行(列)的倍加到另一行(列).
以上三种变换称为矩阵的初等行(列)变换,且分别称为倍乘、互换、倍加初等行(列)变换。

我们可以通过上面三个简单的变换手段来把矩阵变换为可逆矩阵，这些过程写成数学表达就是初等矩阵的乘积
若 是可逆矩阵,则 可以表示成有限个初等矩阵的乘积,即 ,其中 是初等矩阵

若 可逆,则 一定可以通过若干(有限)次初等行变换化为同阶单位矩阵 ,即

对行的变换，在数学表达上，表达为在矩阵的左侧乘

对列的变换，就是在这个矩阵的右侧乘

互换类型的初等矩阵的逆，矩阵不变

倍加类型的初等矩阵的逆就是加上原来的相反倍数

某行（列）乘以k的初等矩阵的逆，矩阵变为乘以k分之一

线代入门笔记

对换矩阵

倍乘矩阵

倍加矩阵

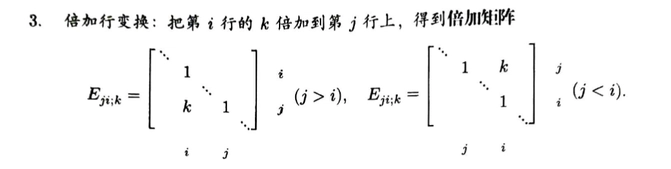
Thm

我们还可以考虑初等列变换．根据前面的分析，我们容易得到上述初等矩阵左（右）乘与初等行（列）变换之间的对应关系，即“左行右列”

还记得

Transclude of 矩阵的逆-入门#^b83354

这个结论吗，根据上面左行右列的论断，可以得到

Thm

1. 若矩阵 Im 经过某一初等行变换得到矩阵 T, 则任意 m x n 矩阵 A 经过相同初等行变换得到矩阵 TA

2. 若矩阵 In 经过某一初等列变换得到矩阵 T, 则任意 mxn 矩阵 A 经过相同初等列变换得到矩阵 AT.

现在，站在初等矩阵的视角下看求解线性方程组-入门的问题，我们可以有新的认识了
线性代数入门, page 63
因此，我们利用 Gauss 消元法或 Gauss-Jordan 消元法求解线性方程组 ,就是找到一系列初等矩阵，使得矩阵是阶梯形矩阵或行简化阶梯形矩阵.
而对任意初等矩阵，定理 1.3.4 说明了与同解
我们知道，这些方法能够求解线性方程组，根本原因在于初等变换可逆.
那么初等变换诱导的线性变换，作为线性映射可逆吗？这又对应了初等矩阵的什么性质？

注意这句：