题44
题目
Q:【2021 统考真题】使用 Dijkstra 算法求下图中从顶点 1 到其余各顶点的最短路径将当前找到的从顶点 1 到顶点 2,3,4,5 的最短路径长度保存在数组 dist 中, 求出第二条最短路径后, dist 中的内容更新为 ( ).
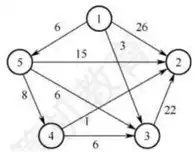
A. 26,3,14,6
B. 25,3,14,6
C. 21,3,14,6
D. 15,3,14,6
分析
A:和这个题29是一样的,要明确这里的路径和目标点的概念是什么
注意这里到达2有一条从左侧迂回的路径,dist数组里面的第一个元素就是从源点1到达2的最短路径的长度,也就是21
解
C
在执行 Dijkstra 算法时,首先初始化 dist[] ,若顶点 1 到顶点 i(i = 2,3,4,5) 有边,就初始化为边的权值; 若无边,就初始化为 ∞ ; 初始化顶点集 S 只含顶点 1 。Dijkstra 算法每次选择一个到顶点 1 距离最近的顶点 j 加入顶点集 S ,并判断由顶点 1 绕行顶点 j 后到任意一个顶点 k 是否距离更短,若距离更短 (即 dist[j] + arcs[j][k] < dist[k] ),则将 dist[x] 更新为 dist[j] + arcs[j][k] ; 重复该过程,直至所有顶点都加入顶点集 S 。数组 dist 的变化过程如下图所示,可知将第二个顶点 5 加入顶点集 S 后,数组 dist 更新为 {21},3,{14},6 。
// 初始化 dist[]
dist[] = {26, 3, ∞, 6};
// 顶点 3 加入顶点集 S
dist[] = {25, 3, ∞, 6};
// 顶点 5 加入顶点集 S
dist[] = {21, 3, 14, 6};