题35
题目
【2011 统考真题】若一棵二叉树的前序遍历序列和后序遍历序列分别为 1, 2, 3, 4 和 4, 3, 2, 1,则该二叉树的中序遍历序列不会是( )。
A. 1, 2, 3, 4
B. 2, 3, 4, 1
C. 3, 2, 4, 1
D. 4, 3, 2, 1
分析
中序遍历加上前序或者后续可以唯一确定一个树
可以试选项
解
C
前序序列为 NLR, 后序序列为 LRN, 由于前序序列和后序序列刚好相反, 所以不可能存在一个结点同时有左右孩子, 即二叉树的高度为 4。
1 为根结点, 由于根结点只能有左孩子 (或右孩子), 因此在中序序列中, 1 或在序列首或在序列尾, 选项 A、B、C、D 皆满足要求。
仅考虑以 1 的孩子结点 2 为根结点的子树, 它也只能有左孩子 (或右孩子), 因此在中序序列中, 2 或在序列首或在序列尾, 选项 A、B、D 皆满足要求。
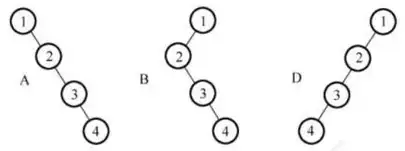
【另解】画出各选项与题干信息所对应的二叉树如下, 所以 A、B、D 均满足。