题19

题19

题目

【2022 统考真题】已知非空二叉树 的结点值均为正整数,采用顺序存储方式保存,数据结构定义如下:

typedef struct {
    // MAX_SIZE 为已定义常量
    int SqBiTNode[MAX_SIZE]; // 保存二叉树结点值的数组
    int ElemNum; // 实际占用的数组元素个数
} SqBiTree;

中不存在的结点在数组 SqBiTNode 中用 -1 表示。例如,对于下图所示的两棵非空二叉树 和

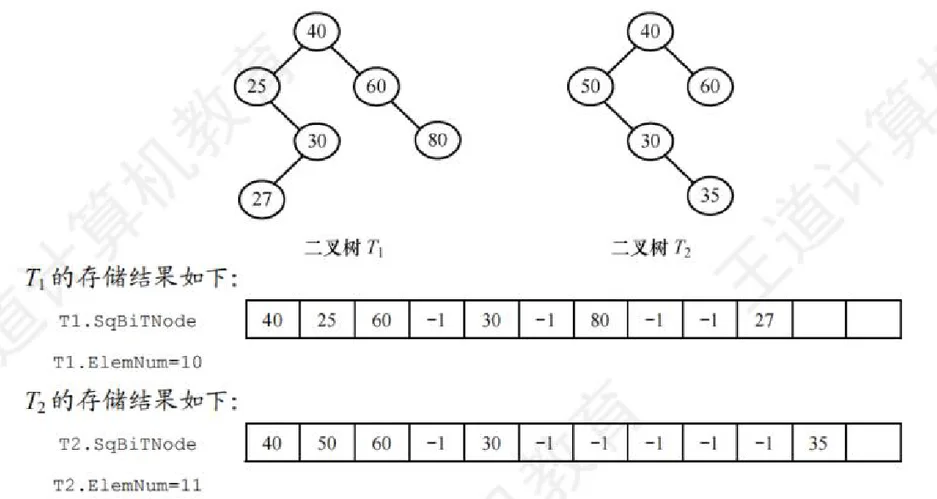
请设计一个尽可能高效的算法, 判定一棵采用这种方式存储的二叉树是否为二叉搜索树, 若是, 则返回 true, 否则, 返回 false。要求:

1. 给出算法的基本设计思想。
2. 根据设计思想, 采用 C 或 C++ 语言描述算法, 关键之处给出注释。

分析

解

19.【解答 1】

1. 算法的基本设计思想。

对于采用顺序存储方式保存的二叉树, 根结点保存在 SqBiTNode [0] 中; 当某结点保存在 SqBiTNode [i]中时, 若有左孩子, 则其值保存在 SqBiTNode [2i+1]中; 若有右孩子, 则其值保存在 SqBiTNode [21+2] 中; 若有双亲结点, 则其值保存在 SqBiTNode [ (i-1) /2] 中。

二叉搜索树需要满足的条件是: 任意一个结点值大于其左子树中的全部结点值, 小于其右子树中的全部结点值。中序遍历二叉搜索树得到一个升序序列。

使用整型变量 val 记录中序遍历过程中已遍历结点的最大值, 初值为一个负整数。若当前遍历的结点值小于或等于 val, 则算法返回 false, 否则, 将 val 的值更新为当前结点的值。

2. 算法实现

#define false 0
#define true 1
 
typedef int bool;
 
bool judgeInOrderBST(SqBiTree bt, int k, int *val) { //初始调用时 k 的值是 0
if (k < bt.ElemNum && bt.SqBiTNode[k] != -1) {
        if (!judgeInOrderBST(bt, 2 * k + 1, val)) return false;
        if (bt.SqBiTNode[k] <= *val) return false;
        *val = bt.SqBiTNode[k];
        if (!judgeInOrderBST(bt, 2 * k + 2, val)) return false;
    }
    return true;
}

【解答 2】

1. 算法的基本设计思想。

对于采用顺序存储方式保存的二叉树, 根结点保存在 SqBiTNode[0]中; 当某结点保存在 SqBiTNode [i] 中时, 若有左孩子, 则其值保存在 SqBiTNode [2i+1] 中; 若有右孩子, 则其值保存在 SqBiTNode [21+2] 中; 若有双亲结点, 则其值保存在 SqBiTNode [ (i-1) /2] 中。

二叉搜索树需要满足的条件是: 任意一个结点值大于其左子树中的全部结点值, 小于其右子树中的全部结点值。设置两个数组 pmax 和 pmin。根据二叉搜索树的定义, SqBiTNode [i] 中的值应该大于以 SqBiTNode [21+1] 为根的子树中的最大值 (保存在 pmax [21+1] 中), 小于以 SqBiTNode [21+2] 为根的子树中的最小值 (保存在 pmin[21+1] 中)。初始时, 用数组 SqBiTNode 中前 ElemNum 个元素的值对数组 pmax 和 pmin 初始化。

在数组 SqBiTNode 中从后向前扫描, 扫描过程中逐一验证结点与子树之间是否满足上述的大小关系。

2. 算法实现。

#define false 0
#define true 1
 
typedef int bool;
 
bool judgeBST(SqBiTree bt) {
    int k, m;
    int *pmin, *pmax;
 
    pmin = (int *)malloc(sizeof(int) * bt.ElemNum);
    pmax = (int *)malloc(sizeof(int) * bt.ElemNum);
 
    for (k = 0; k < bt.ElemNum; k++) { // 辅助数组初始化
        pmin[k] = pmax[k] = bt.SqBiTNode[k];
    }
 
    for (k = bt.ElemNum - 1; k > 0; k--) { // 从最后一个叶结点向根遍历
        if (bt.SqBiTNode[k] != -1) {
            m = (k - 1) / 2; // 双亲
 
            if (k % 2 == 1 && bt.SqBiTNode[m] > pmax[k]) { // 其为左孩子
                pmin[m] = pmin[k];
            } else if (k % 2 == 0 && bt.SqBiTNode[m] < pmin[k]) { // 其为右孩子
                pmax[m] = pmax[k];
            } else {
                return false;
            }
        }
    }
 
    return true;
}