浮点数的表示形式和表示范围
定点数表示回顾
Q: 定点小数在计算机中的表示形式是什么?
A: 定点小数由一个符号位和 N 个数值位构成,小数点位置固定在符号位和数值位之间。
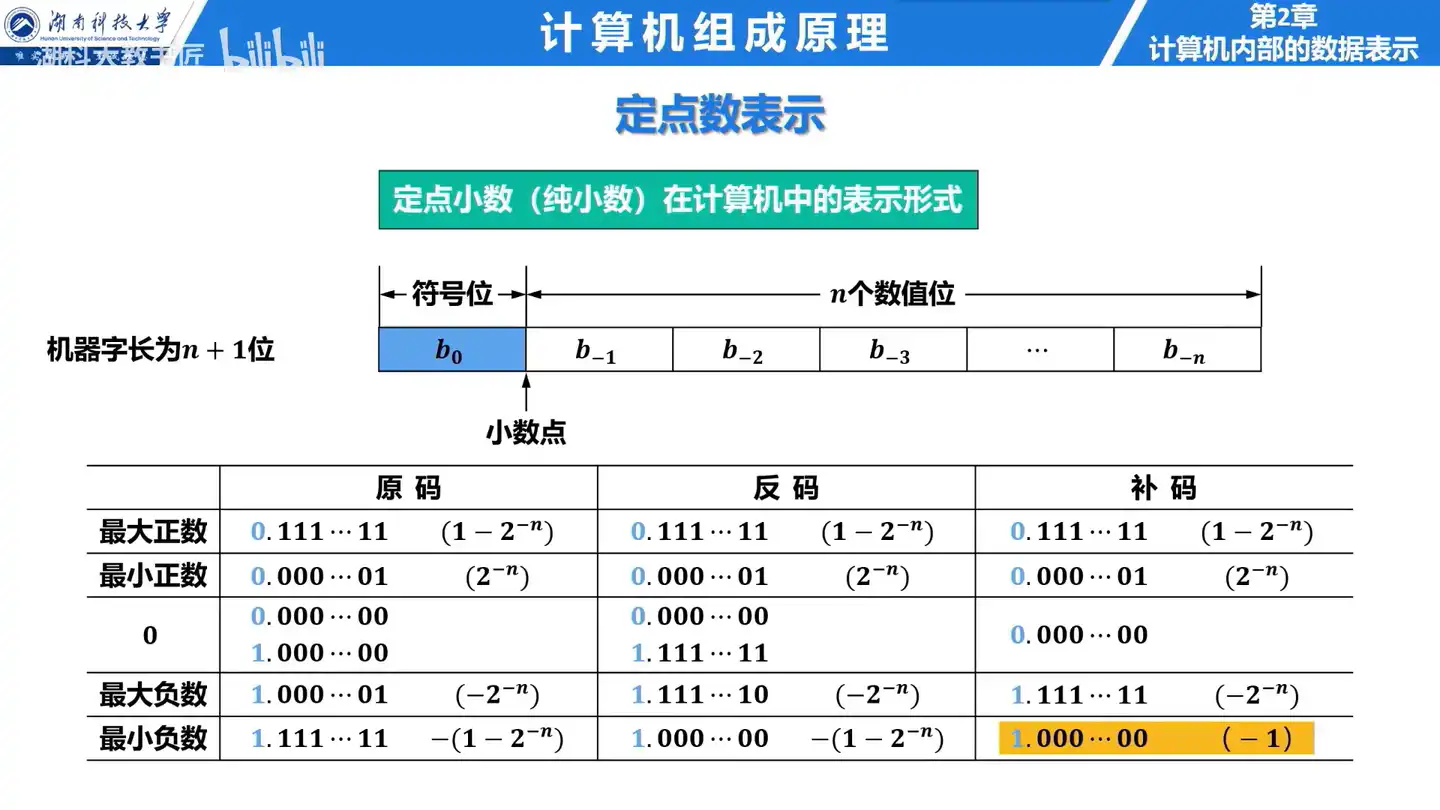
Q: 定点小数的机器码表示范围是什么?
A: 
- 零的原码表示有两种。
- 最小正数的值为
。 - 最大正数的值为
。
也就是整数的绝对值部分,现在把他放到了小数点后面去,最大最小也就是一点
浮点数的表示
Q: 浮点数的表示形式是什么?
A: 浮点数由阶码 E 和尾数 M 两部分构成,阶码用定点整数表示,尾数用定点小数表示。
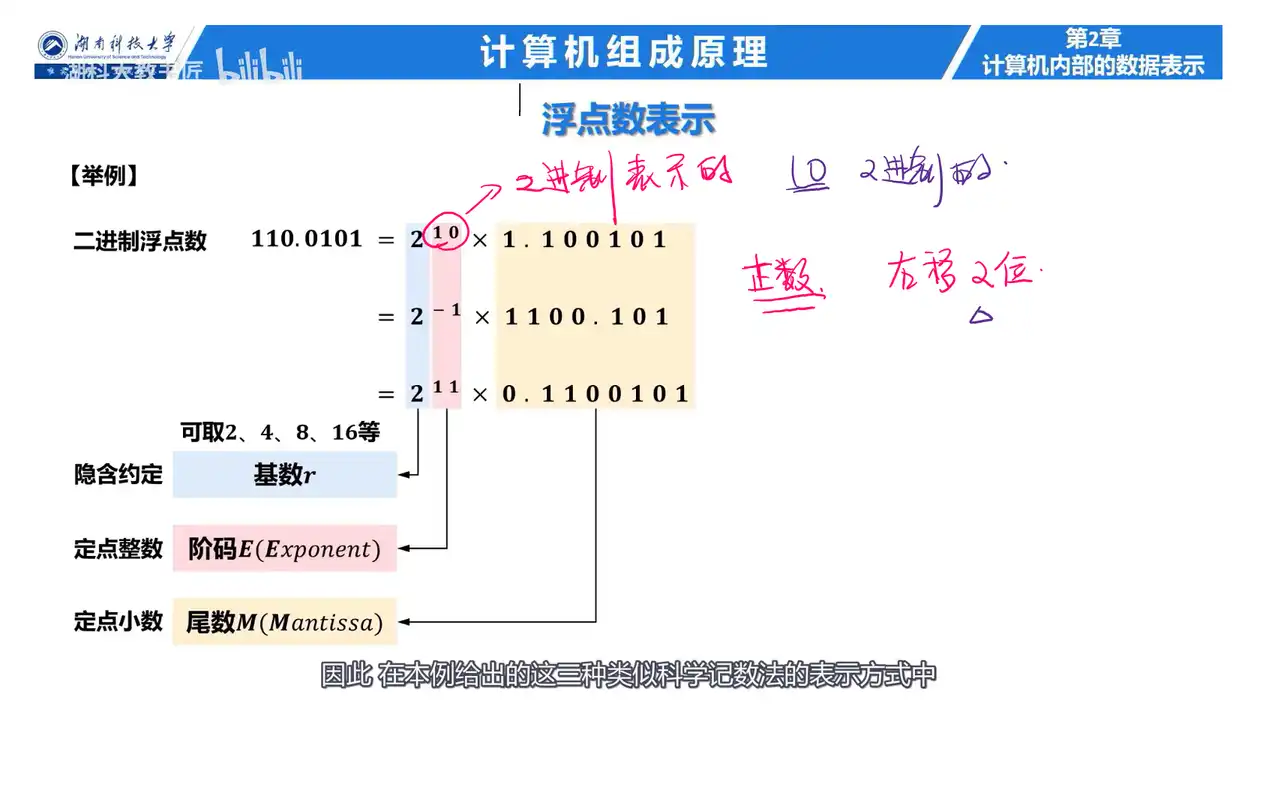
只有最后这个表达形式符合,因为后面卡其色覆盖的部分得是一定点小数
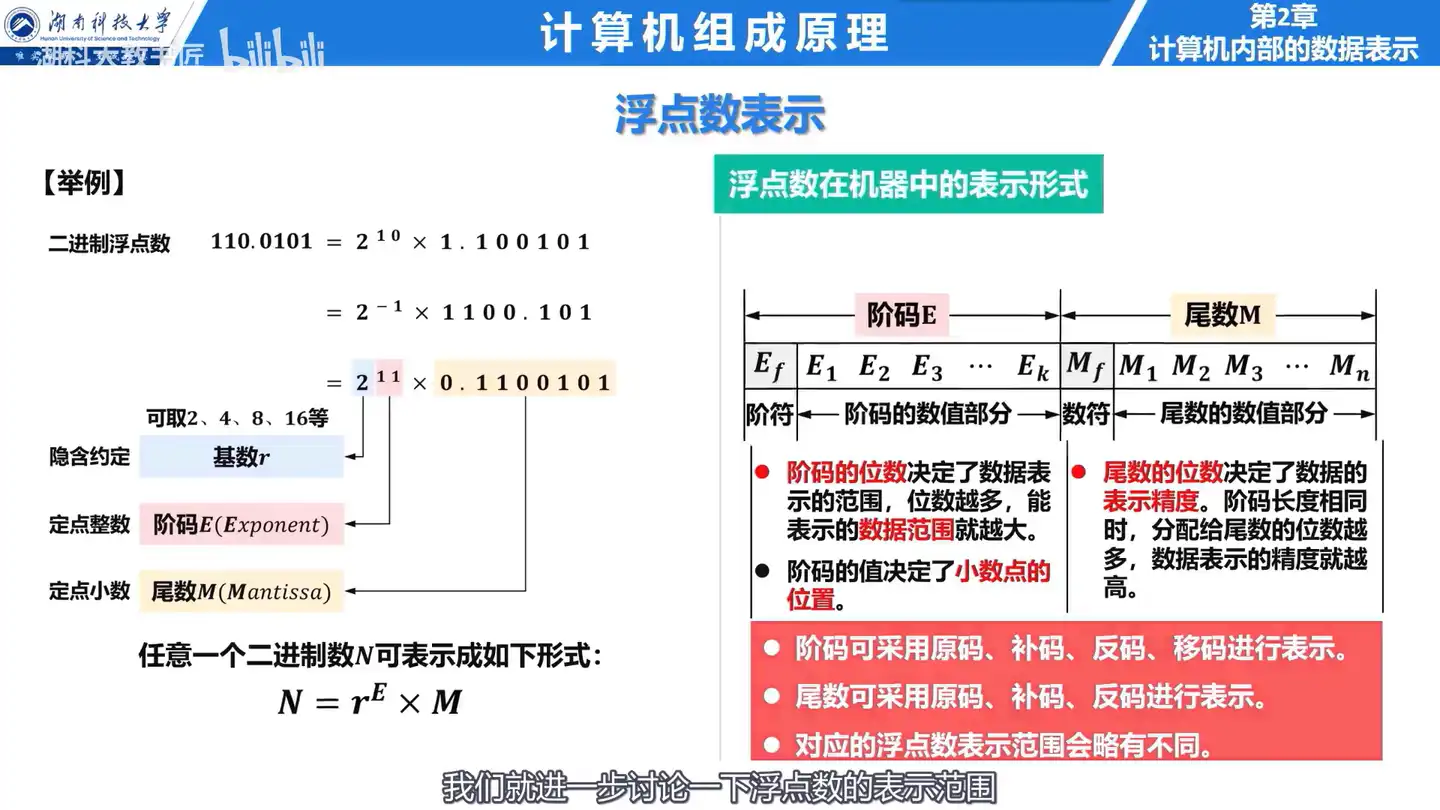
Q: 浮点数(单精度和双精度)的阶码和尾数分别由多少个二进制位构成?
A: 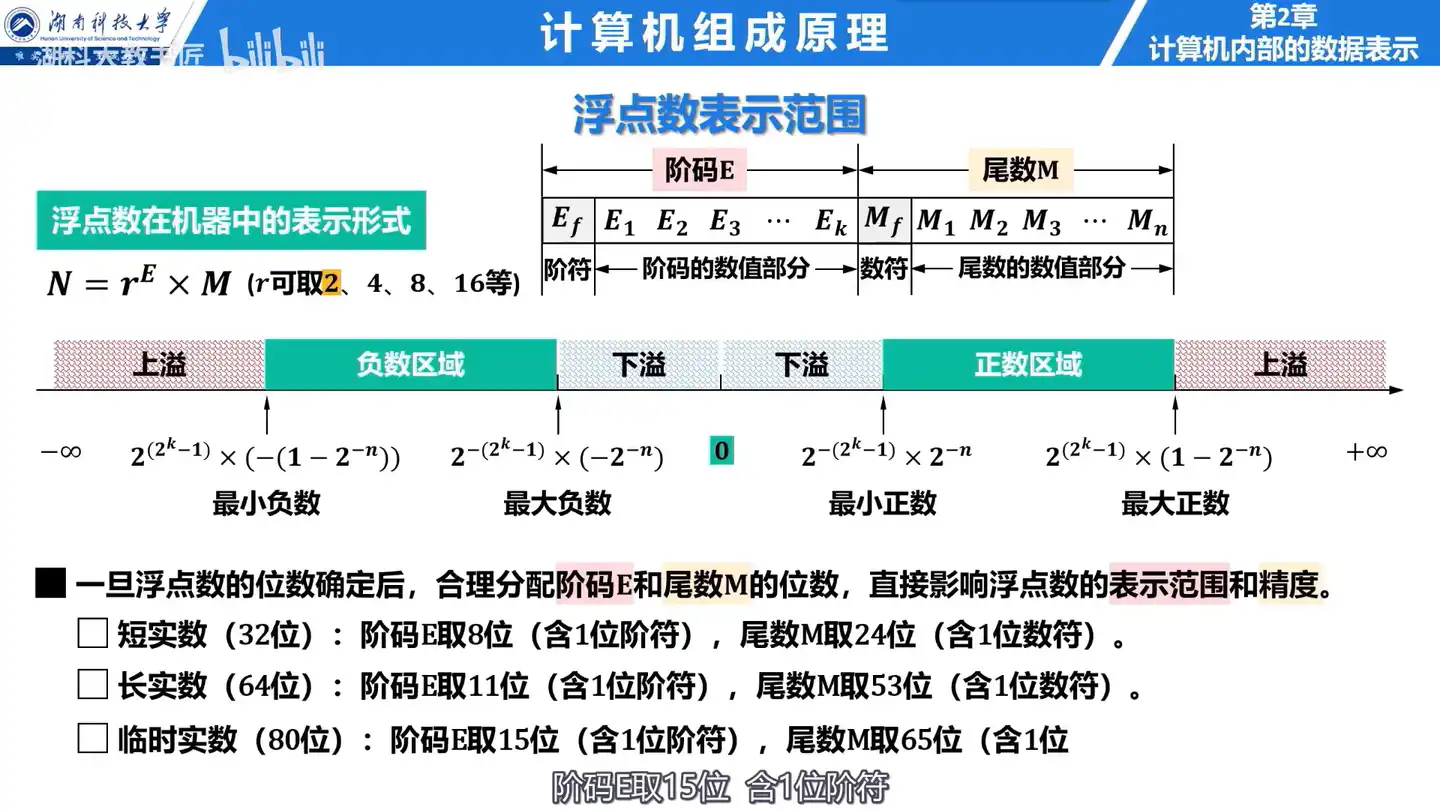
- 单精度数(32 位):阶码 8 位,尾数 24 位。
- 双精度数(64 位):阶码 11 位,尾数 53 位。
浮点数的表示范围
Q: 浮点数的表示范围如何确定?
A: 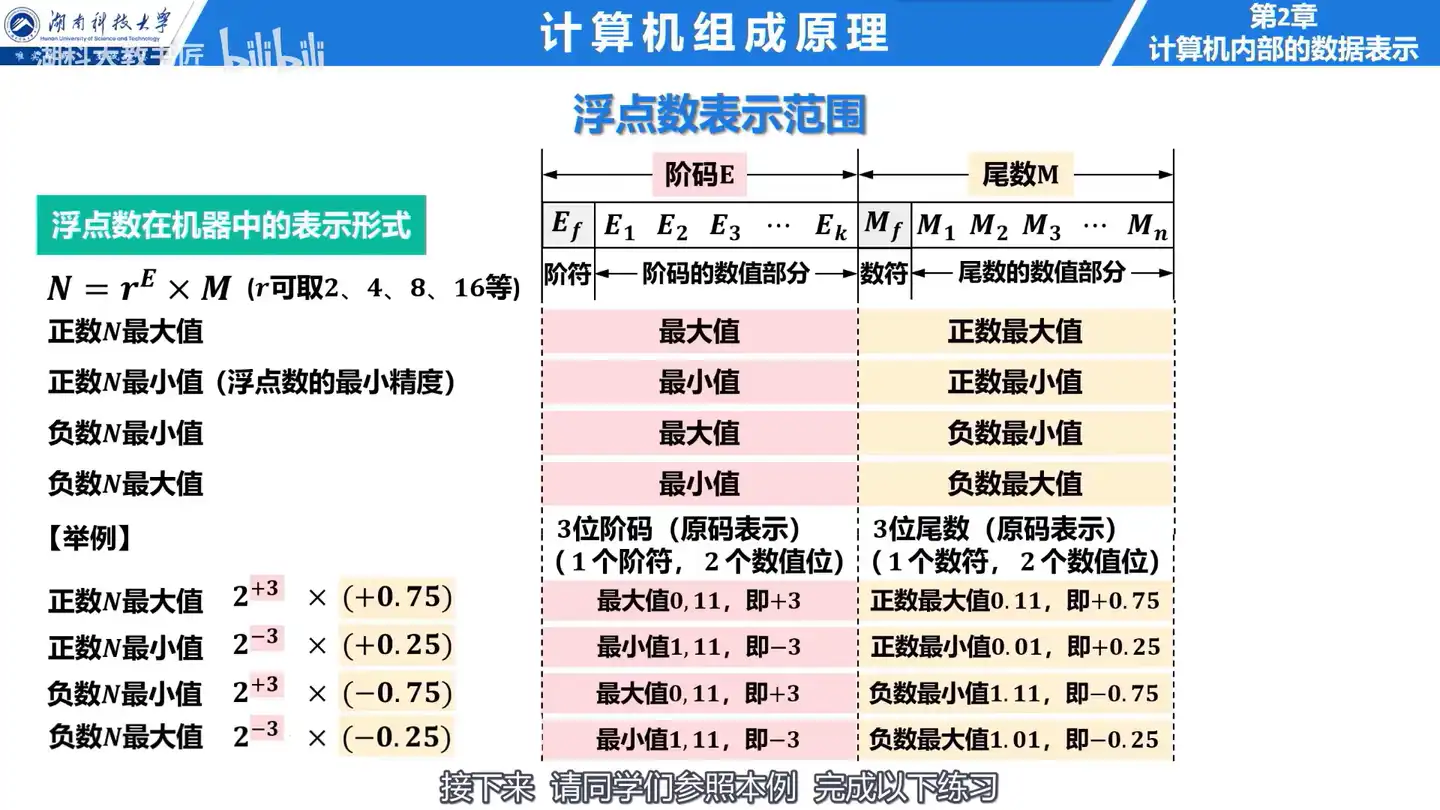
- 最大正数:阶码最大值,尾数最大值。
- 最小正数:阶码最小值,尾数最小值。
- 最大负数:阶码最大值,尾数最小值。
- 最小负数:阶码最小值,尾数最大值。
浮点数的溢出
Q: 什么是浮点数的上溢和下溢?
A: 
- 上溢:当浮点数的阶码大于最大阶码时,机器停止运算,显示溢出标志。
- 下溢:当浮点数的阶码小于最小阶码时,数据不能被精确表示,通常将尾数各位强制为零。
浮点数的规格化
浮点数规格化的必要性
Q: 为什么需要对浮点数进行规格化?
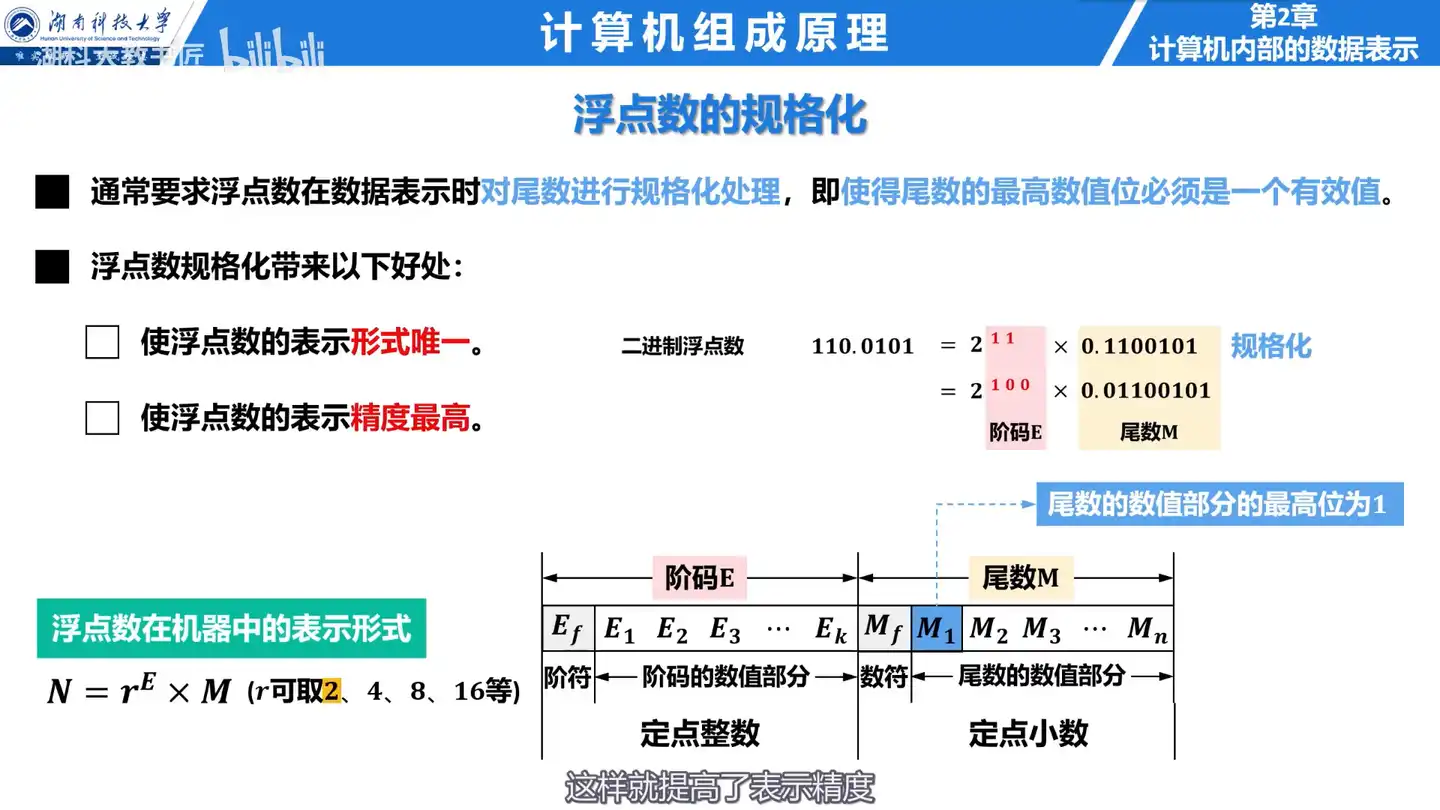
A: 浮点数的规格化可以使得浮点数的表示形式唯一,并提高表示精度,避免不同表示形式带来的混乱。
规格化方法
Q: 浮点数(二进制)的规格化方法有哪些?
A: 左归:尾数数值部分每左移一位,阶码减一。

右归:尾数数值部分每右移一位,阶码加一。

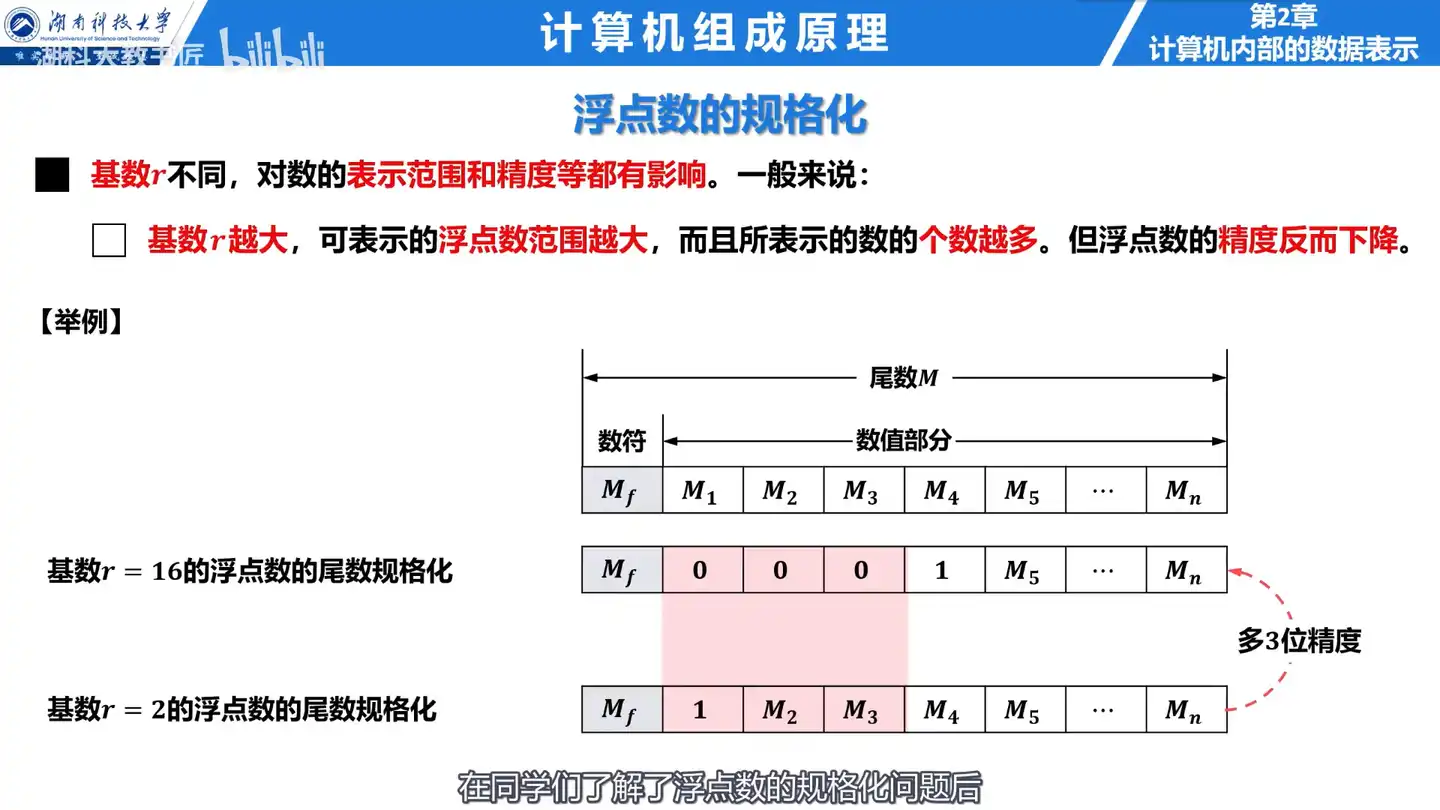
Q:基数r和浮点数的精度的关系是怎么样的?
A:基数r越大,可表示的浮点数范围越大,而且所表示的数的个数越多,但浮点数的精度反而下降
规格化对浮点数的影响
Q: 规格化对浮点数的表示范围和精度有什么影响?
A: 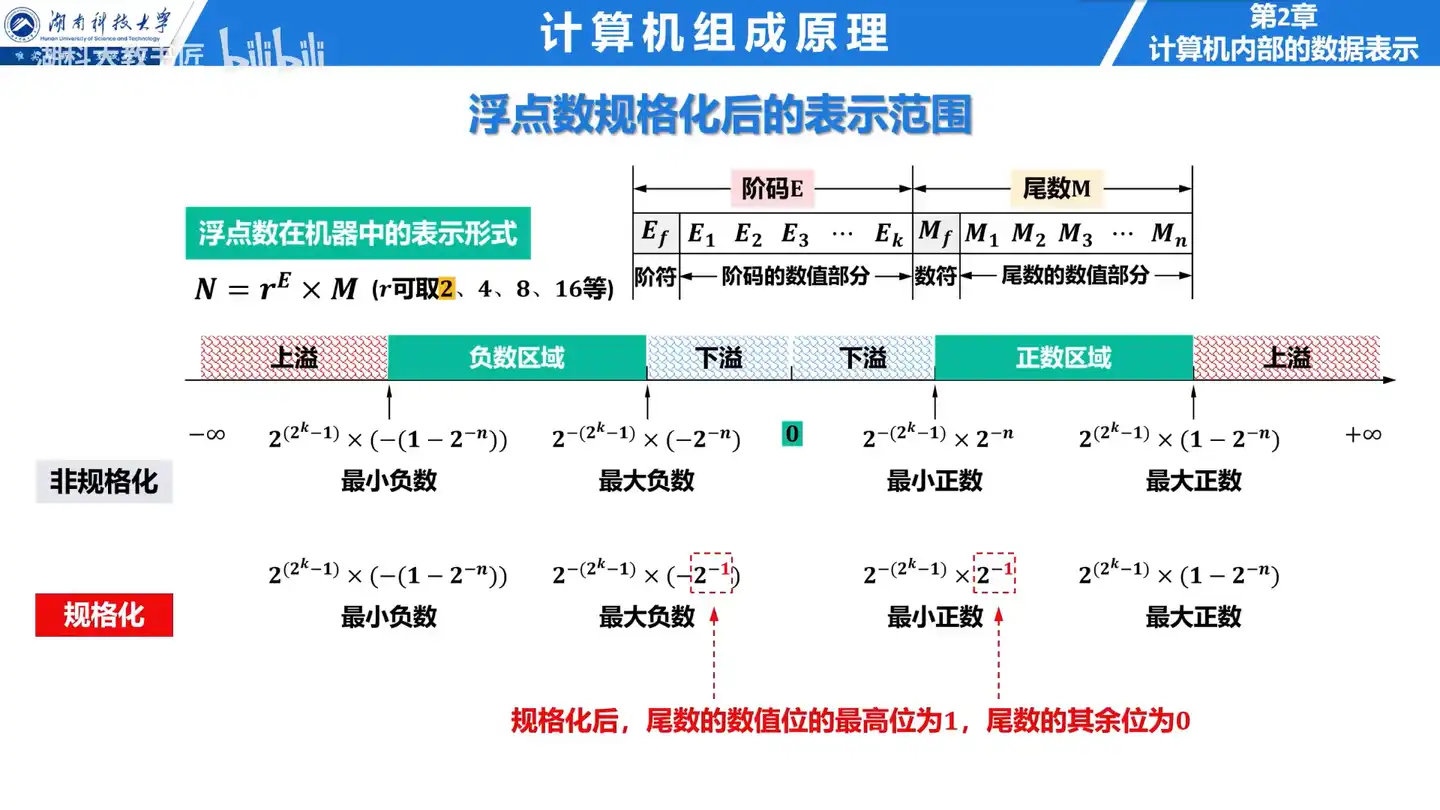
- 规格化后,浮点数的表示范围不变,但可以提高精度。
- 尾数的最高位为一,避免了无效的零。
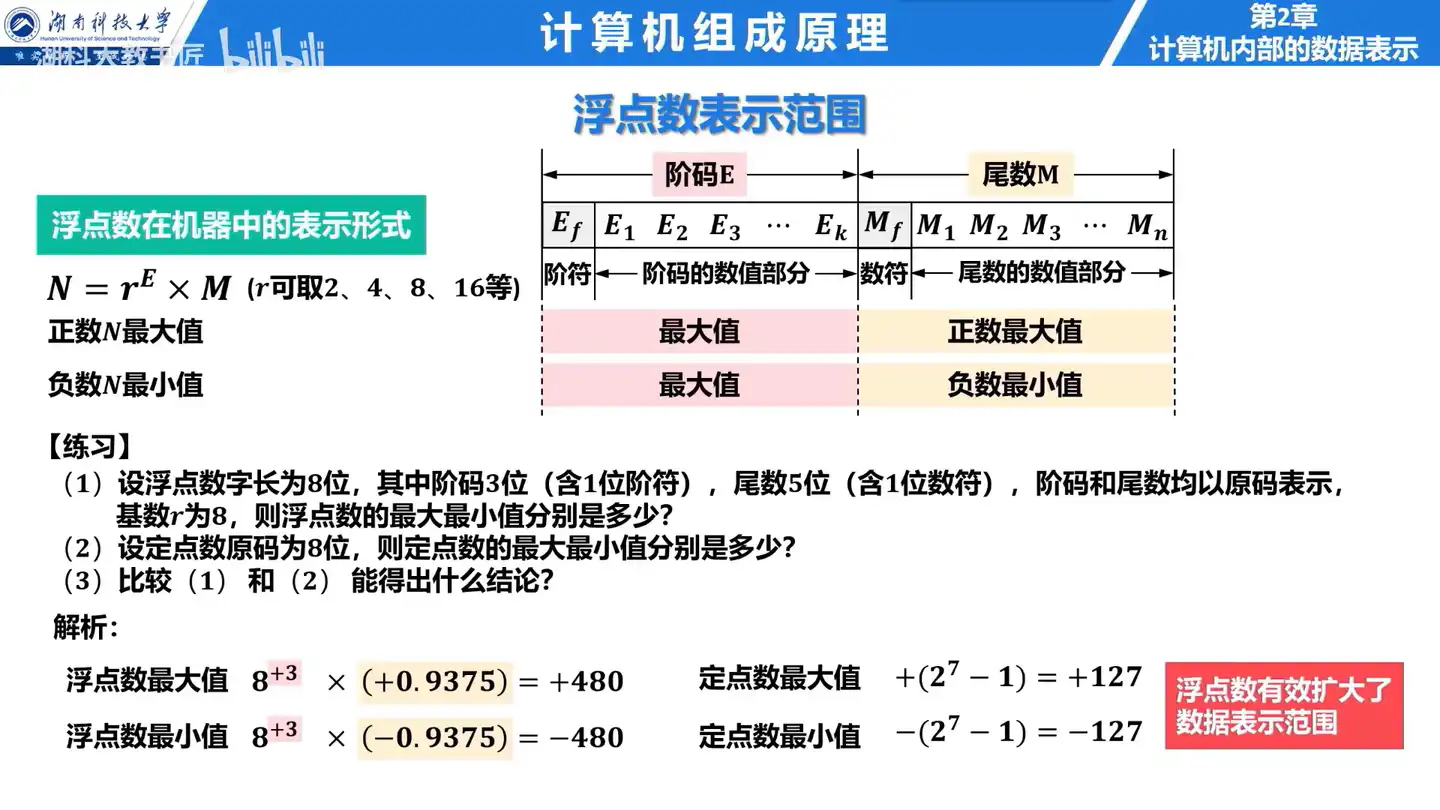
Q:设浮点数字长为16位,其中阶码5位(含1位阶符),尾数11位(含1位数符),将十进制数-56写成二进制定点数和浮点数(要求规格化表示),并分别写出它们各自的机器数(原码、反码、补码)形式。

A: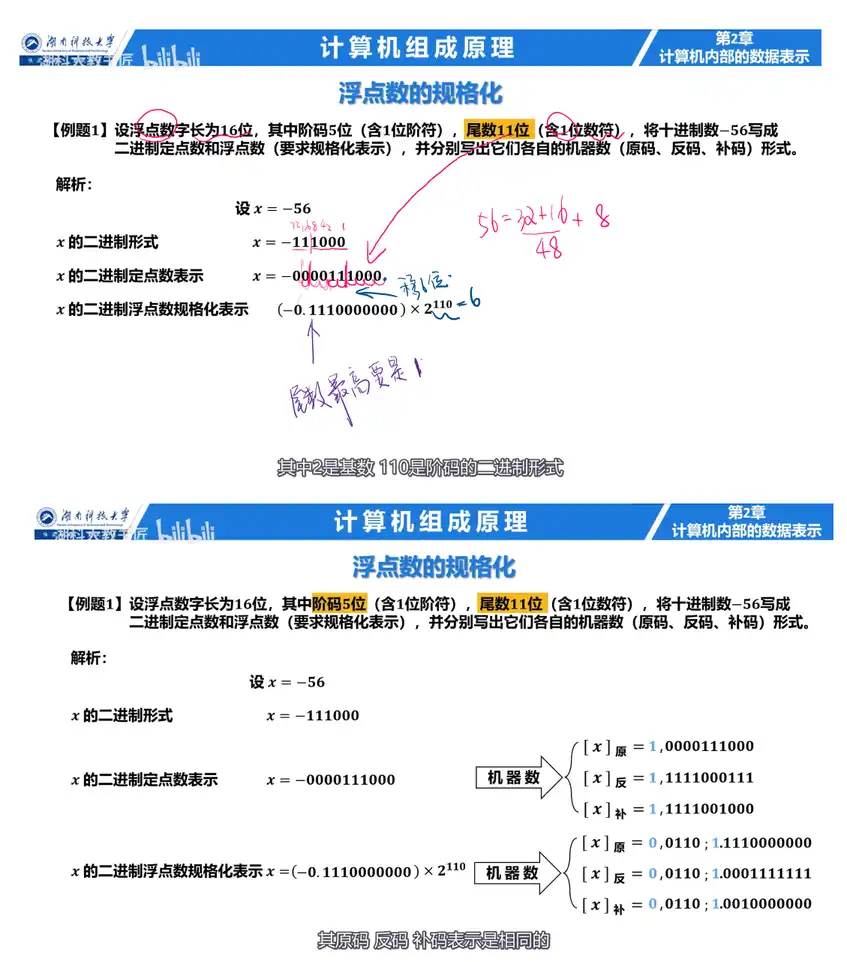
计算机组成原理微课堂 - IEEE754 浮点数标准
IEEE754 浮点数标准简介
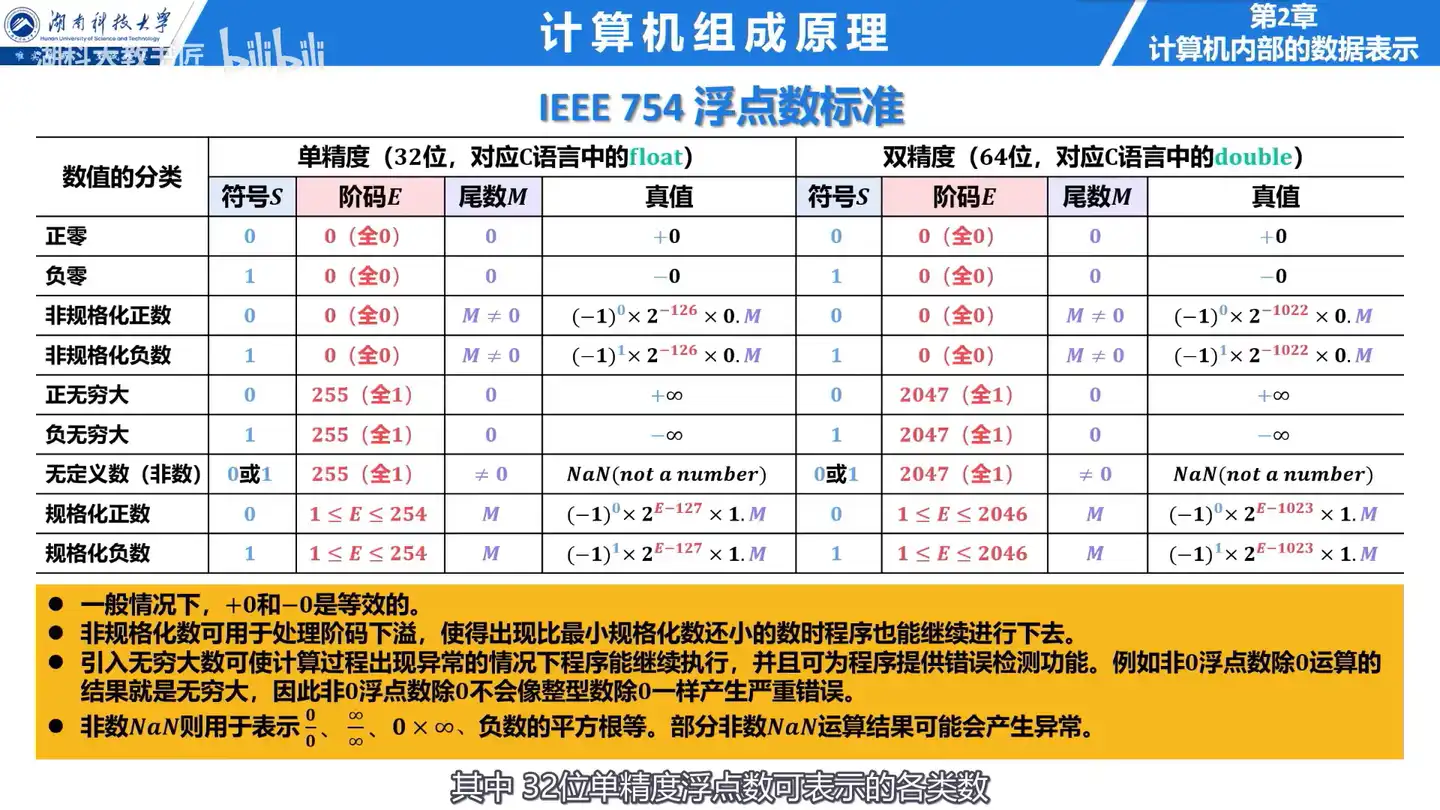
Q: IEEE754 标准包含哪些基本的浮点数格式?
A: IEEE754 标准包含两种基本的浮点数格式:
- 32 位单精度浮点数 (float)
- 64 位双精度浮点数 (double)
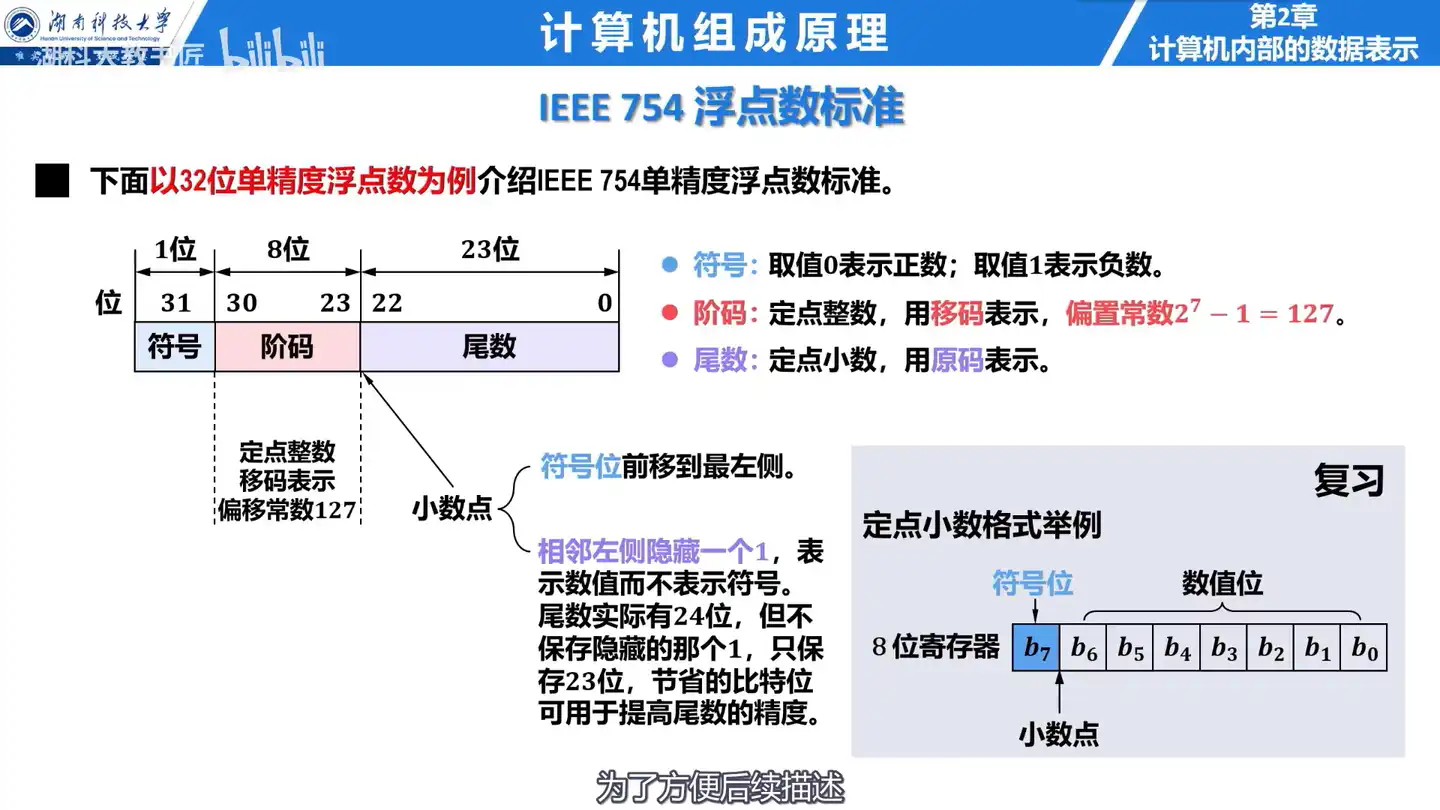
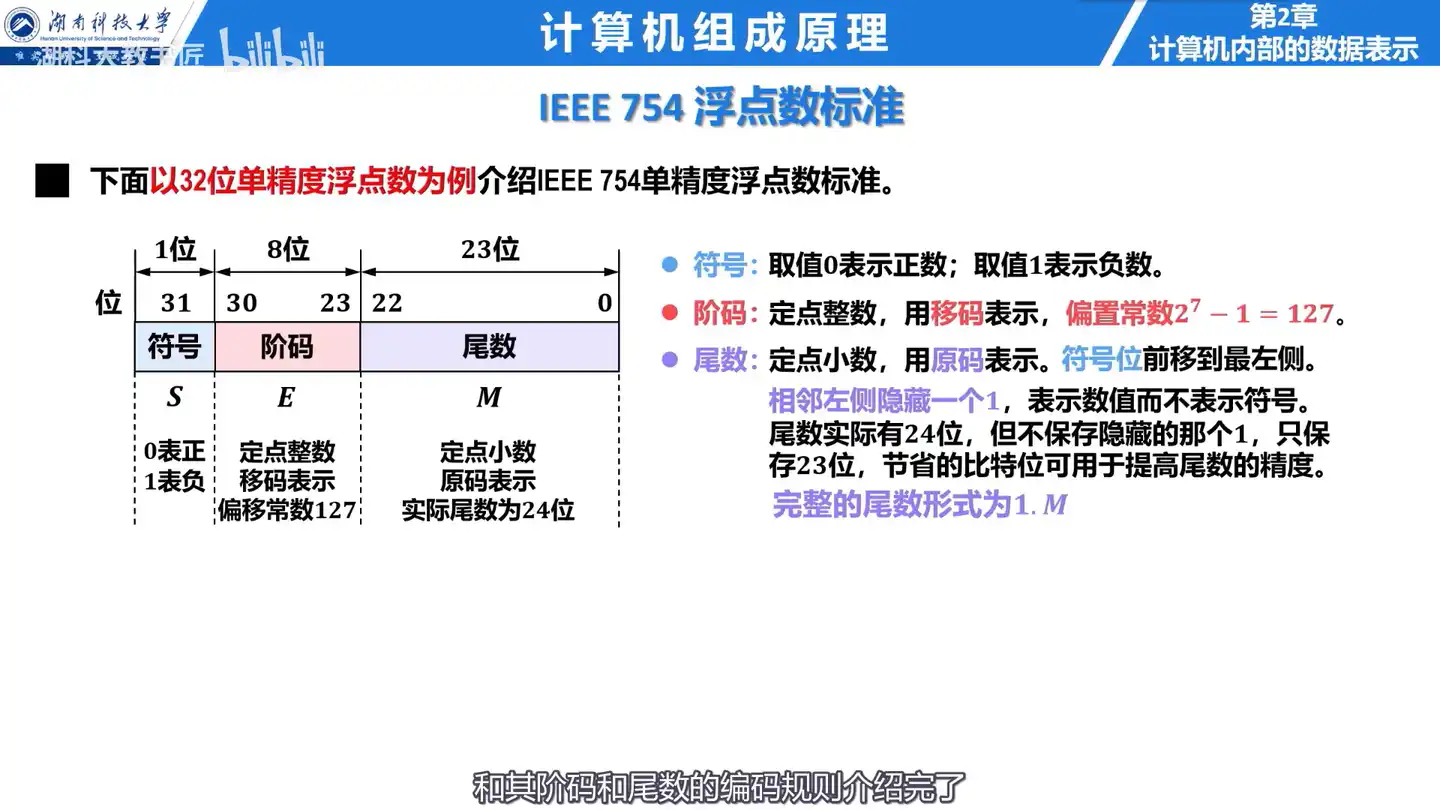
Q: IEEE754 浮点数格式由哪几部分构成?
A: IEEE754 浮点数格式由符号、阶码以及尾数三部分构成。

IEEE754 单精度浮点数阶码
Q: IEEE754 单精度浮点数的阶码如何表示?
A: IEEE754 单精度浮点数的阶码占 8 位,采用阶码表示,偏移常数为 127。

Q: 为什么 IEEE754 单精度浮点数的阶码采用偏移常数 127 而不是 128?
A: 
- 将 8 位全一和 8 位全零这两个阶码对应到最小和第二小的两个真值 -128 和 -127 作为特殊用途。
- 采用偏移常数 127 表示的任何一个规格化数的倒数,则不会溢出。
IEEE754 单精度浮点数尾数
Q: IEEE754 单精度浮点数的尾数如何表示?
A: IEEE754 单精度浮点数的尾数占 23 位,采用原码表示,小数点隐含固定在尾数前面,而将原本小数点相邻左侧的符号位前移到最左侧,并在小数点的相邻左侧隐藏一个 1,但用来表示数值,而不表示符号。
IEEE754 单精度浮点数可表示的各种数
Q: IEEE754 单精度浮点数可以表示哪些类型的数?
A: IEEE754 单精度浮点数可以表示:
- 零 (0)
- 无穷大 (+∞, -∞)
- 非数 (NaN)
- 规格化数
- 非规格化数
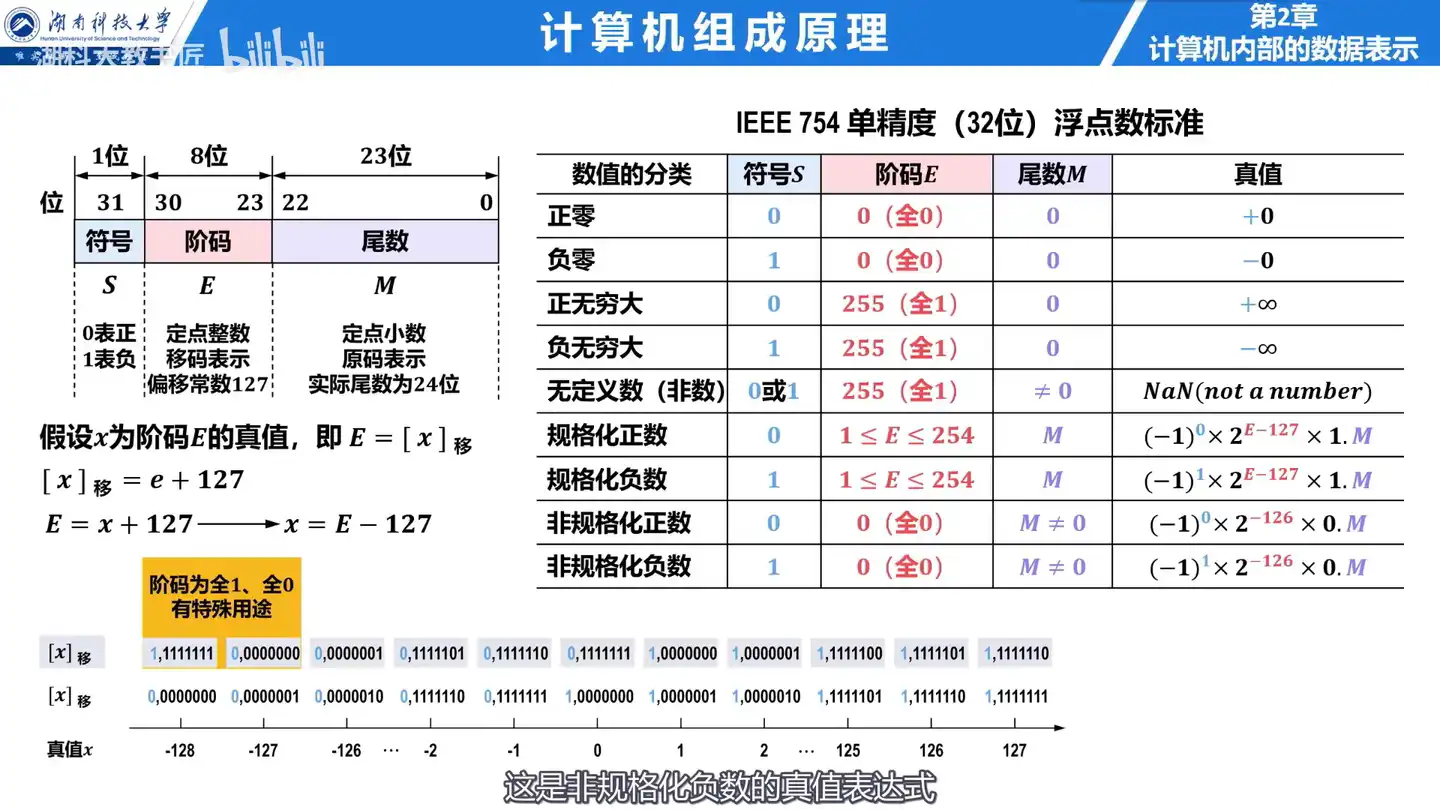
规格化数
Q: 规格化数的定义是什么?
A: 规格化数是指尾数的最高数值位必须是一个有效值。
非规格化数
Q: 非规格化数的定义是什么?
A: 非规格化数是指阶码为 0,尾数不为 0 的数。
也就是用尾数来表达数的大小
Q: 非规格化数的真值表达式是什么?
A:
- 非规格化正数:
(-1)^S * 0.M * 2^(-126) - 非规格化负数:
(-1)^S * 0.M * 2^(-126)

非规格化数可以用于处理阶码下溢,使得出现比最小规格化数还小的的数时程序也能进行下去
IEEE754 单精度浮点数与真值之间的转换
Q: 如何将十进制数转换为 IEEE754 单精度浮点数的 16 进制机器码?
A: 
- 将十进制数转换为二进制形式。
- 将二进制数转换为规格化形式。
- 根据规格化形式,确定符号位、阶码和尾数。
- 将符号位、阶码和尾数合并成 32 位二进制数。
- 将 32 位二进制数转换为 16 进制机器码。
Q: 如何将 IEEE754 单精度浮点数的 16 进制机器码转换为十进制数?
A: 
- 将 16 进制机器码转换为 32 位二进制数。
- 根据 IEEE754 单精度浮点数格式,确定符号位、阶码和尾数。
- 根据阶码和尾数,计算浮点数的真值。
计算机组成原理微课堂 - C语言中的数据类型及转换
计算机中的数据类型
Q: 计算机如何识别数据类型?
A: 计算机本身不识别数据类型,数据类型取决于指令的操作。
整形变量的取值范围
Q: char 型变量的取值范围是什么?
A: 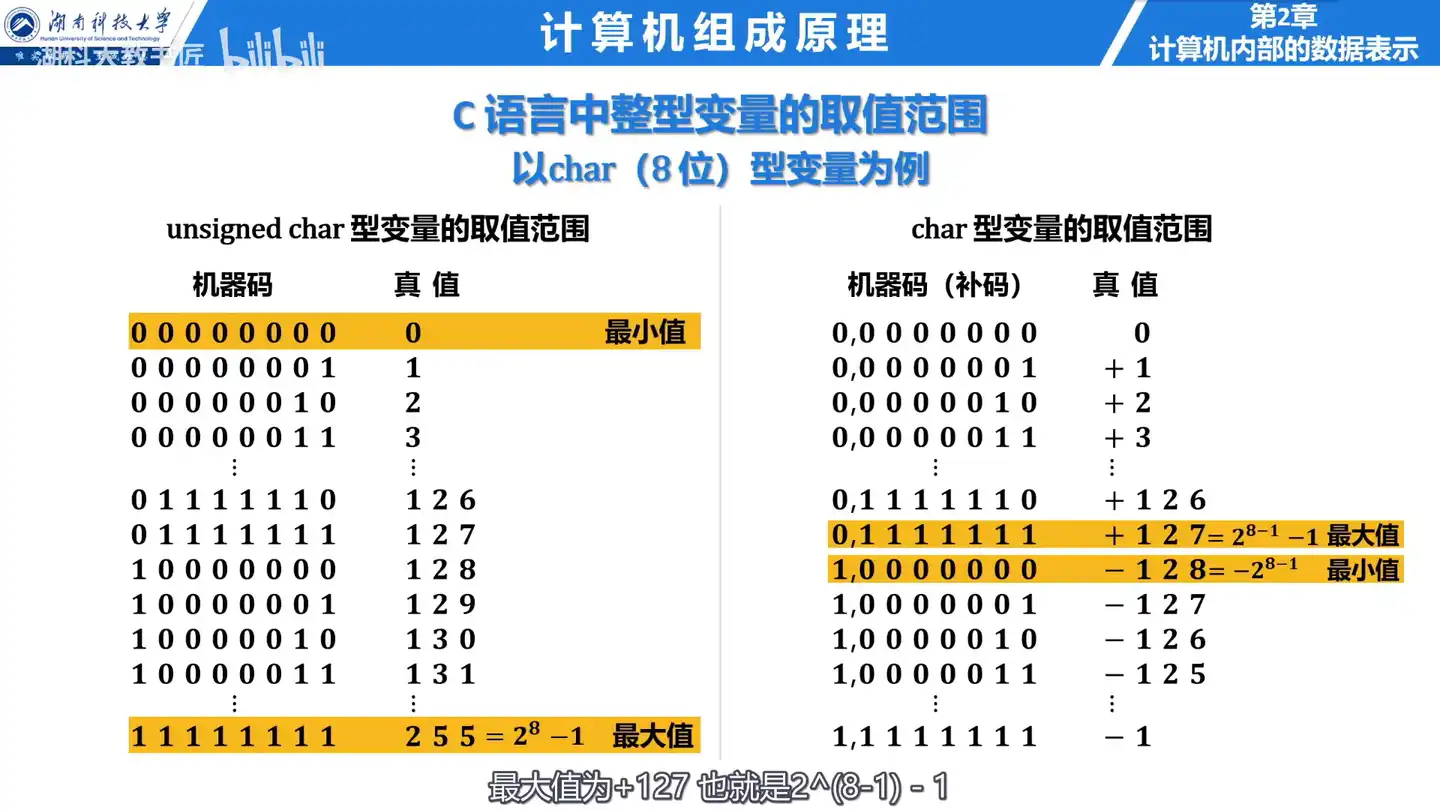
unsigned char: 0 ~ 255char: -128 ~ 127
Q: short 型变量的取值范围是什么?
A: 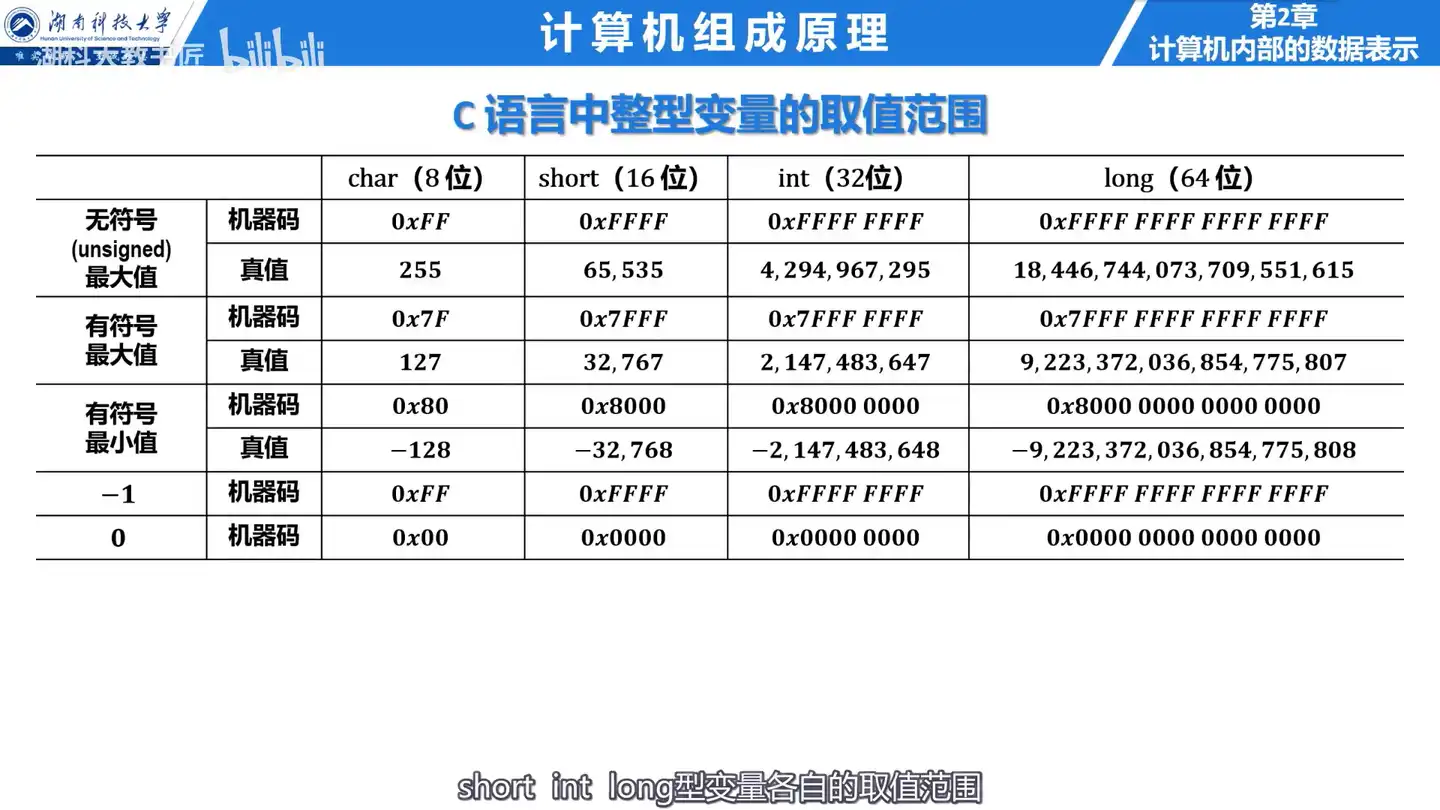
unsigned short: 0 ~ 65535short: -32768 ~ 32767
Q: int 型变量的取值范围是什么?
A: 
unsigned int: 0 ~ 4294967295int: -2147483648 ~ 2147483647
Q: long 型变量的取值范围是什么?
A: 
unsigned long: 0 ~ 18446744073709551615long: -9223372036854775808 ~ 9223372036854775807
C语言中的数据类型转换
Q: C语言中数据类型转换的原则是什么?
A: C语言中数据类型转换的原则尽量保持数的真值不变。

相同字长之间的转换
Q: 相同字长之间的转换如何进行?
A: 相同字长之间的转换只需要保持机器码不变即可。




大字长转小字长
Q: 大字长转小字长时会发生什么?
A: 编译器会将机器码截短处理,可能会导致数据丢失。(向前截断)

int、float、double 型之间的转换
Q: int、float、double 型之间如何进行转换?
A: 编译器只能保证数值尽量相等,大多数情况下只是近似值。
Q: int 转 float 时会发生什么?
A: 比较大的数无法精确表示。
- 不会发生溢出。
- 当 int 型数的第 24 位非 0 时,无法精确转换成 24 位浮点数的尾数,需舍入处理,影响精度。

- 32位int型转换为float型可能有损失
- 判断方法
- 转换为二进制真值
- 写为±1x…x×2^n形式
- 小数点后位数超过23位则损失
Q: int 转 double 时会发生什么?
A: 转换后的数据与原值相同。
- 能保留精确值。

Q: float 转 double 时会发生什么?
A: 转换后的数据与原值相同。
- 能保留精确值。
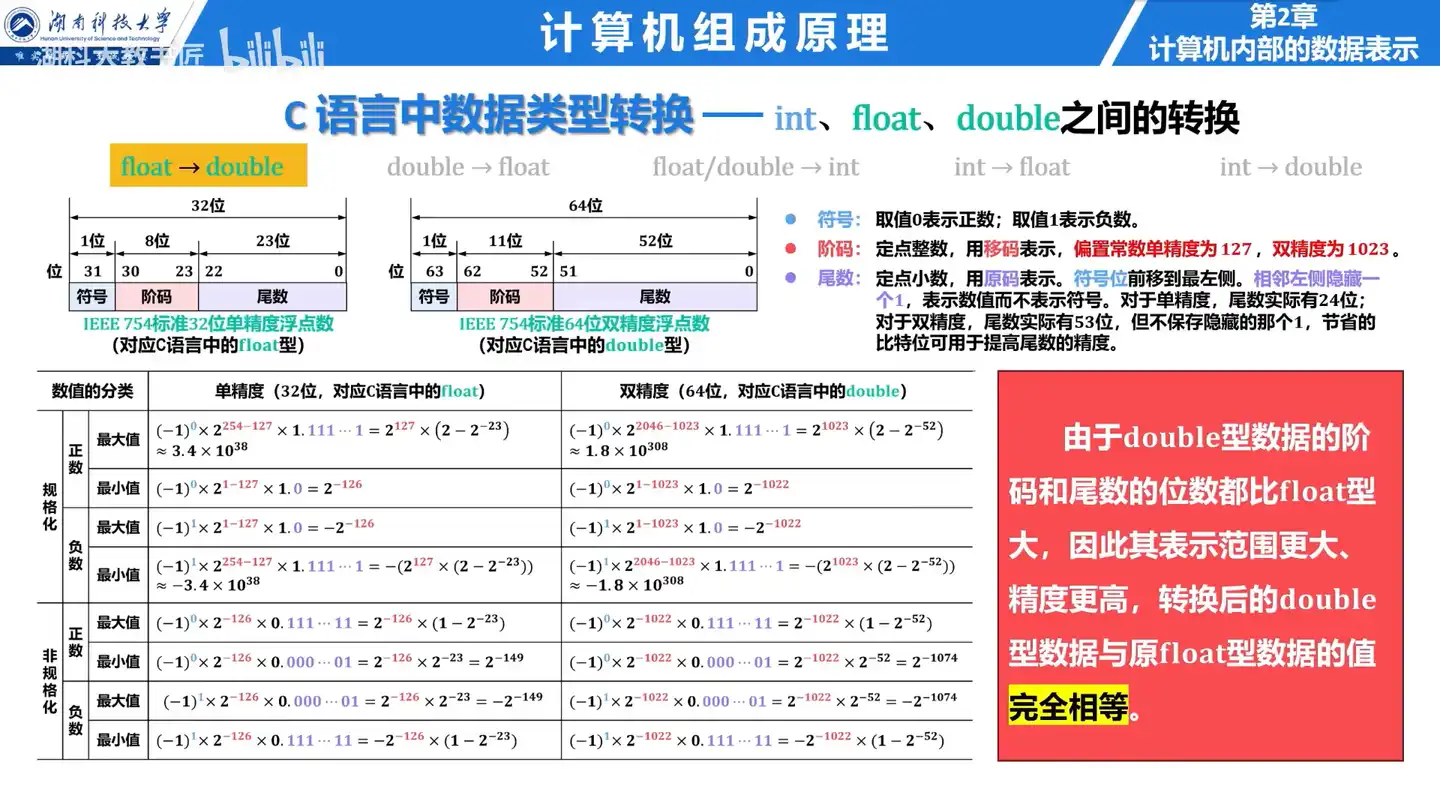
Q: double 转 float 时会发生什么?
A: 大数可能溢出,高精度会发生舍入。
- 大数转换时可能会发生溢出。
- 高精度数转换时会发生舍入。
Q: float 或 double 转 int 时会发生什么?
A: 小数部分被截断,大数可能溢出。
- 数据会向 0 方向截断,发生舍入。
- 大数转换时可能会溢出。

- 小数位部分被舍去
- int型精确到32位整数
- float型保存到1+23位
- 32位int型转换为float型可能有损失
- 判断方法
- 转换为二进制真值
- 写为±1x…x×2^n形式
- 小数点后位数超过23位则损失
总结
Q: C语言中数据类型转换需要注意哪些问题?
A: 
- 相同字长之间的转换,如果数据类型不同,可能会导致数值变化。
- 小字长转大字长,如果原数据为无符号数,则转换后的数据与原值相同;如果原数据为有符号数,则转换后的数据有可能与原值不同。
- 大字长转小字长,可能会导致数据丢失。
- int、float、double 型之间的转换,可能会导致精度缺失或溢出。

计算机组成原理微课堂 - 逻辑移位运算
逻辑移位运算的规则
Q: 逻辑移位运算的规则是什么?
A: 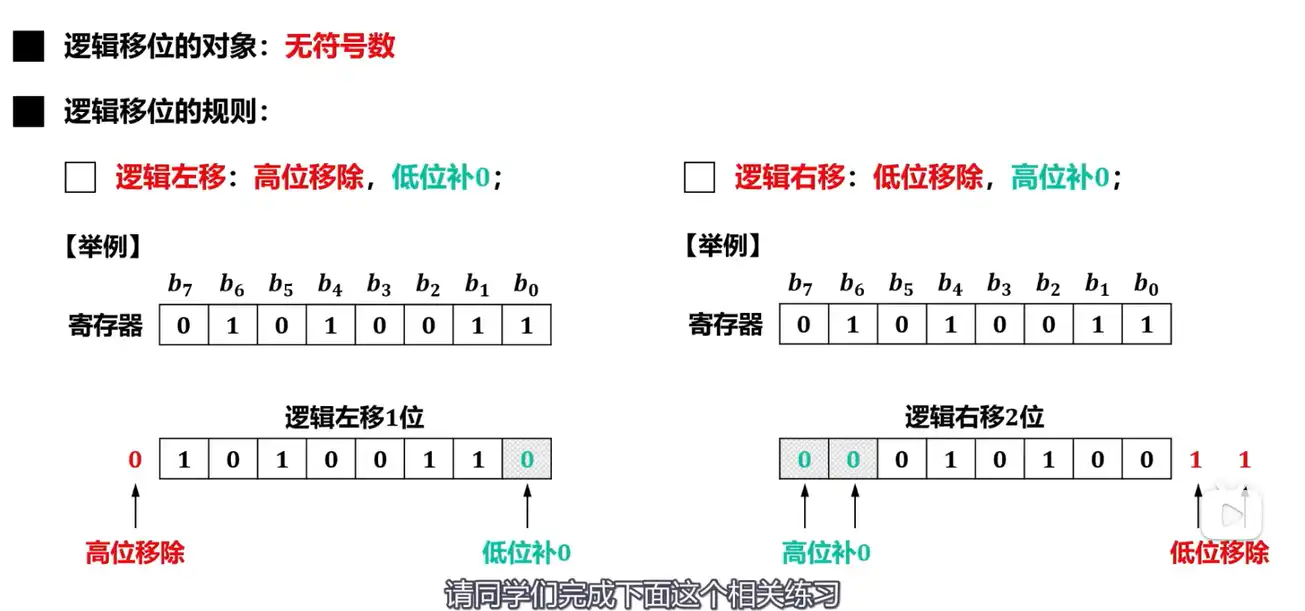
- 逻辑左移:高位移除,低位补零。
- 逻辑右移:低位移除,高位补零。
逻辑移位运算的应用
Q: 逻辑移位运算有什么作用?
A: 逻辑移位运算可以用来:
- 清零寄存器的某个位。
- 将寄存器的某个位置 1。
逻辑移位运算的应用举例
Q: 如何使用逻辑移位运算将寄存器的第六位清零?
A: 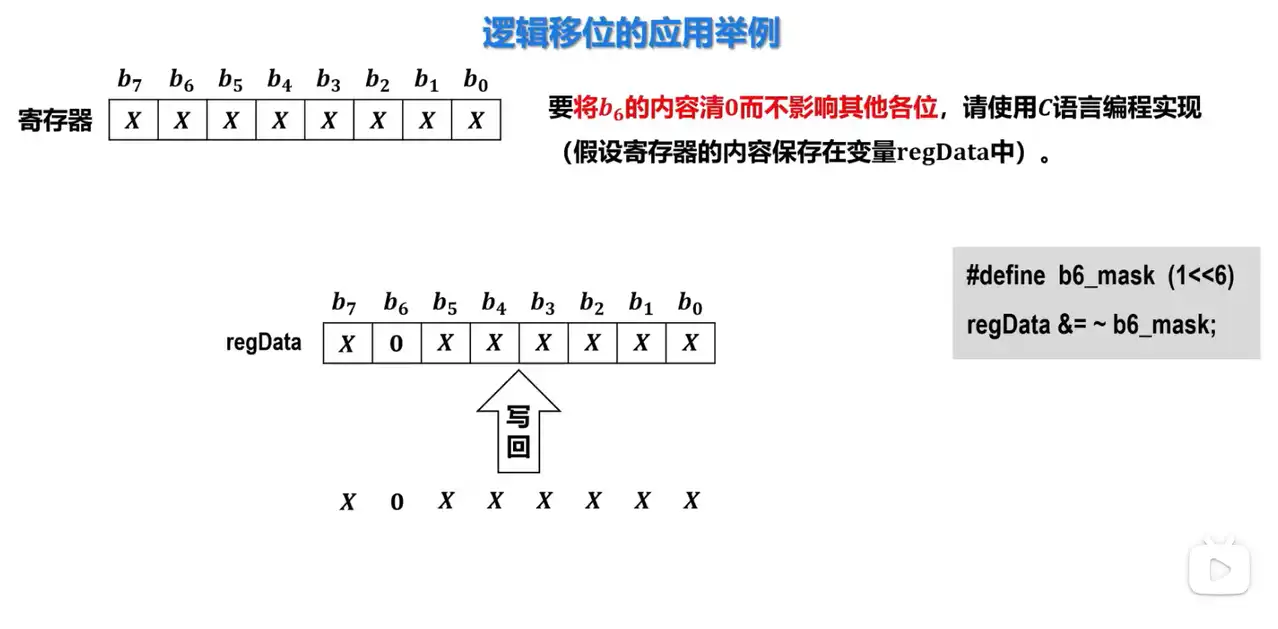
- 定义一个掩码,该掩码的第六位为 1,其他位为 0。
- 将掩码按位取反。
- 将取反后的掩码与寄存器内容进行与运算。
- 将与运算的结果写回寄存器。
Q: 如何使用逻辑移位运算将寄存器的第六位置 1?
A: 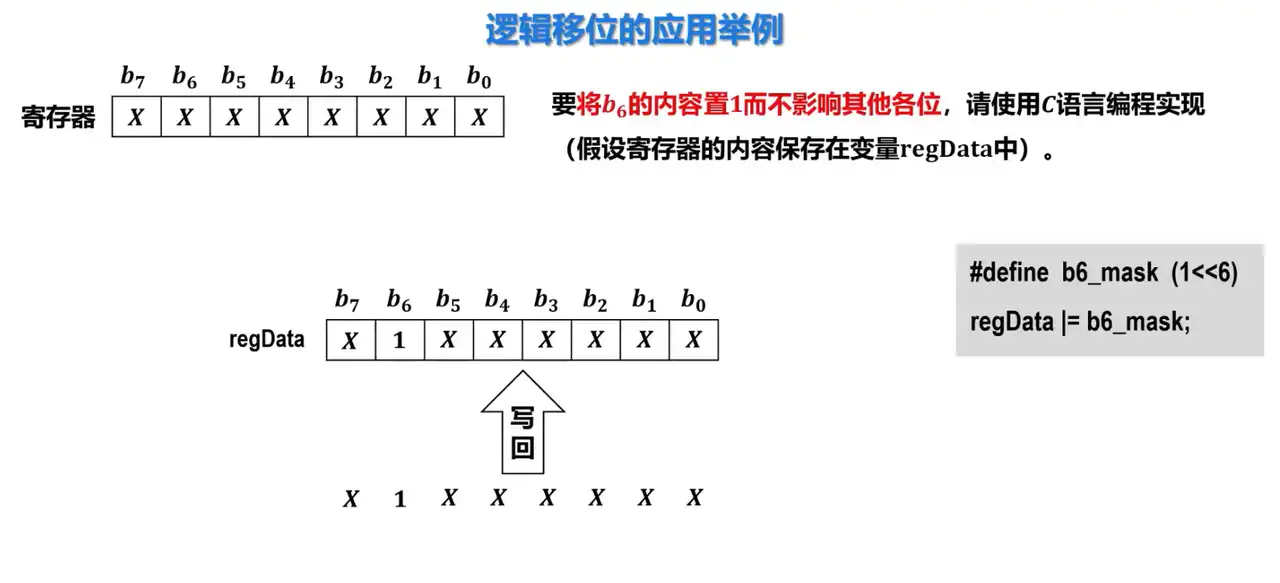
- 定义一个掩码,该掩码的第六位为 1,其他位为 0。
- 将掩码与寄存器内容进行或运算。
- 将或运算的结果写回寄存器。
计算机组成原理微课堂 - 算术移位运算
算术移位运算的规则
Q: 算术移位运算的对象是什么?
A: 算术移位运算的对象是有符号数,包括定点整数和定点小数。

Q: 算术移位运算的规则是什么?
A: 
- 符号位保持不变。
- 仅对数值位进行移位。
- 对于移位后出现的空位,填补规则根据数据类型和移位方向不同而不同。
算术左移
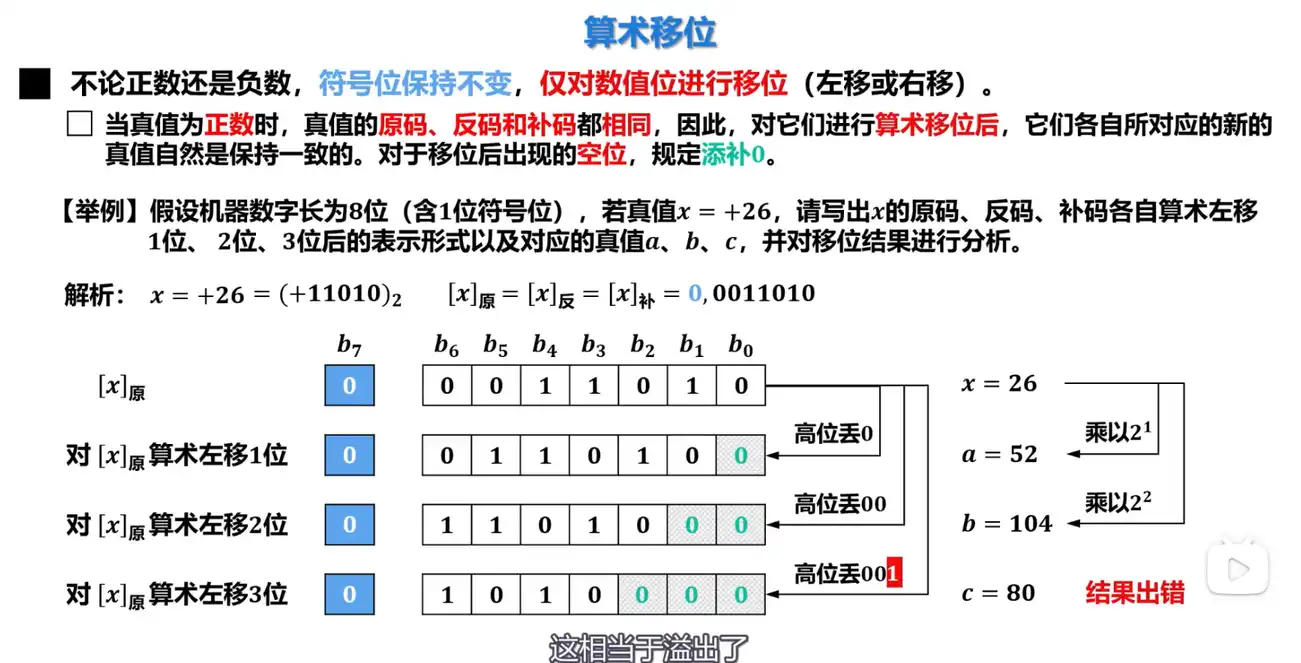
Q: 算术左移的规则是什么?
A: 无论正数还是负数,符号位保持不变,只对数值位进行移位
- 高位移除,低位补零。
- 左移相当于乘以 2 的 N 次方,N 为左移的次数。
- 若最高位丢 1,则结果出错。
算术右移
Q: 算术右移的规则是什么?
A: 无论正数还是负数,符号位保持不变,只对数值位进行移位
- 低位移除,高位填补符号位。
- 右移相当于除以 2 的 N 次方,N 为右移的次数。
- 若最低位丢 1,则结果的精度缺失。
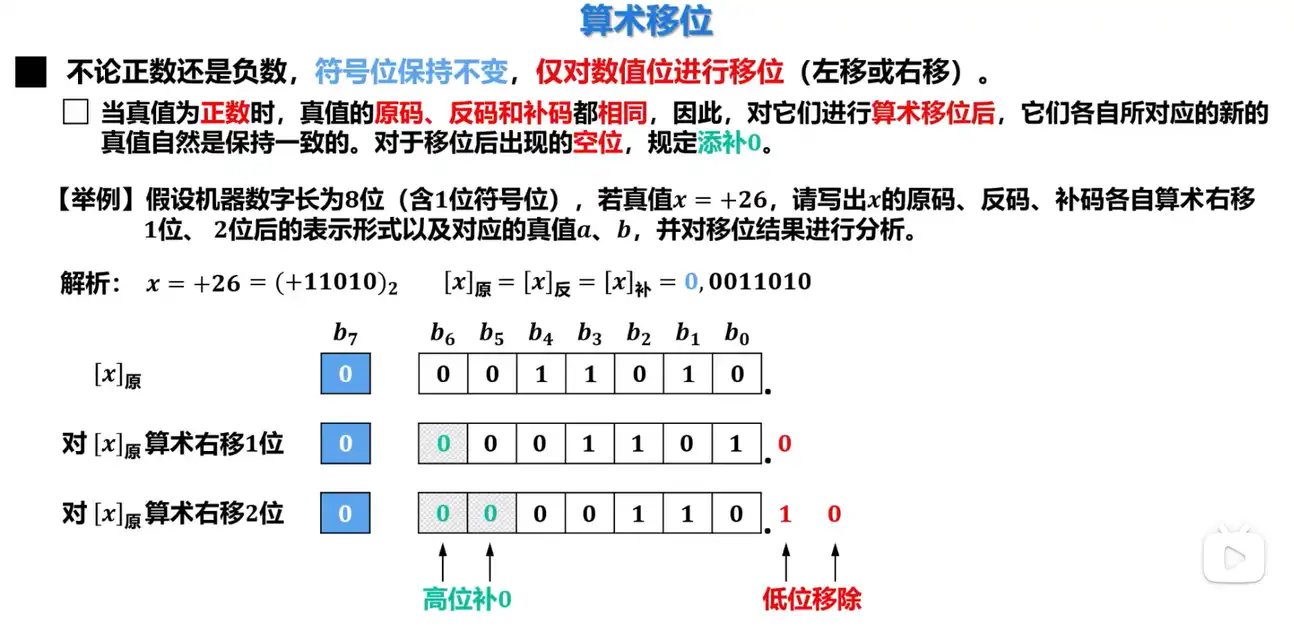
注意这里的这个末尾的小数点

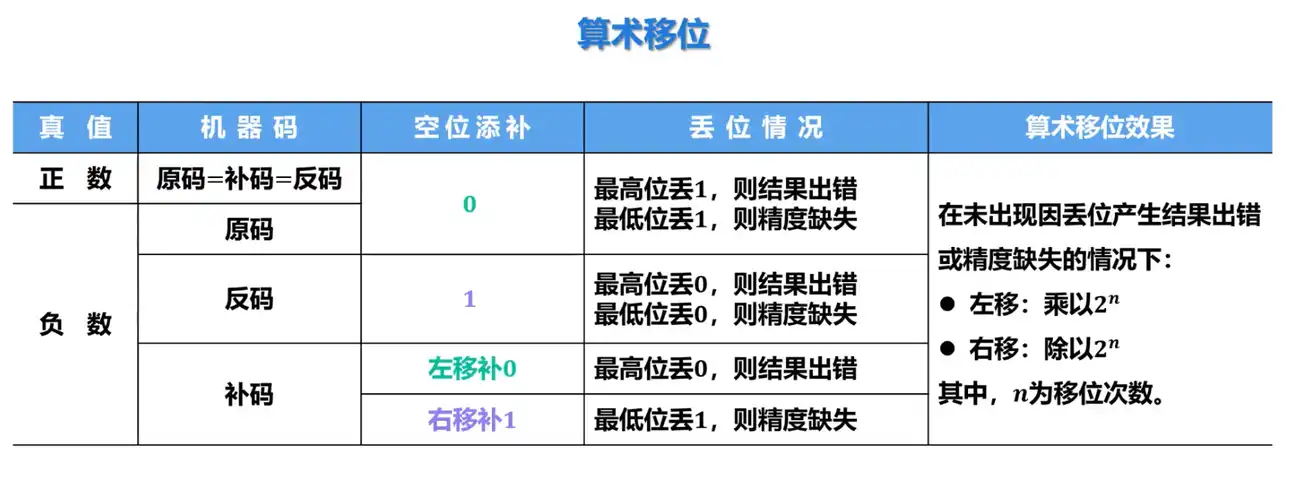
Q: 反码的算术移位规则
A: 和原码的情况相反即可
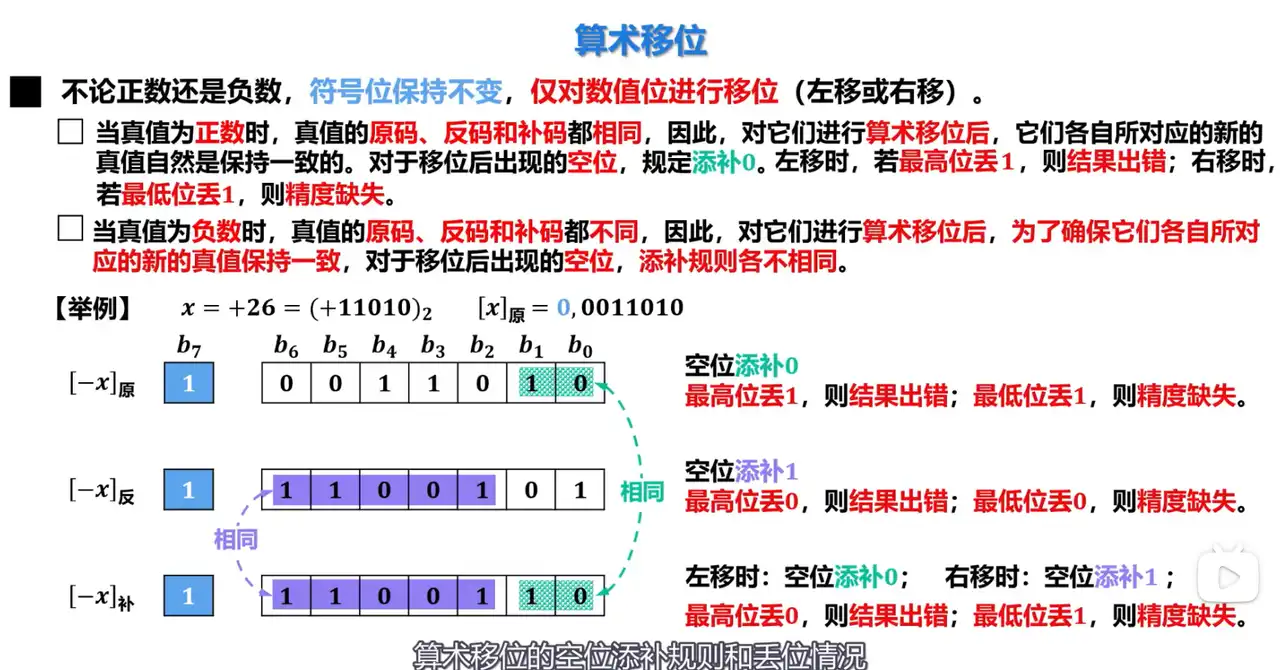
Q:补码的算数移位规则
A:左移补充0,右移补充1

补码的另一种算术移位方法
Q: 补码的另一种算术移位方法,也就是”符号位也参与移位”,是什么?
A: 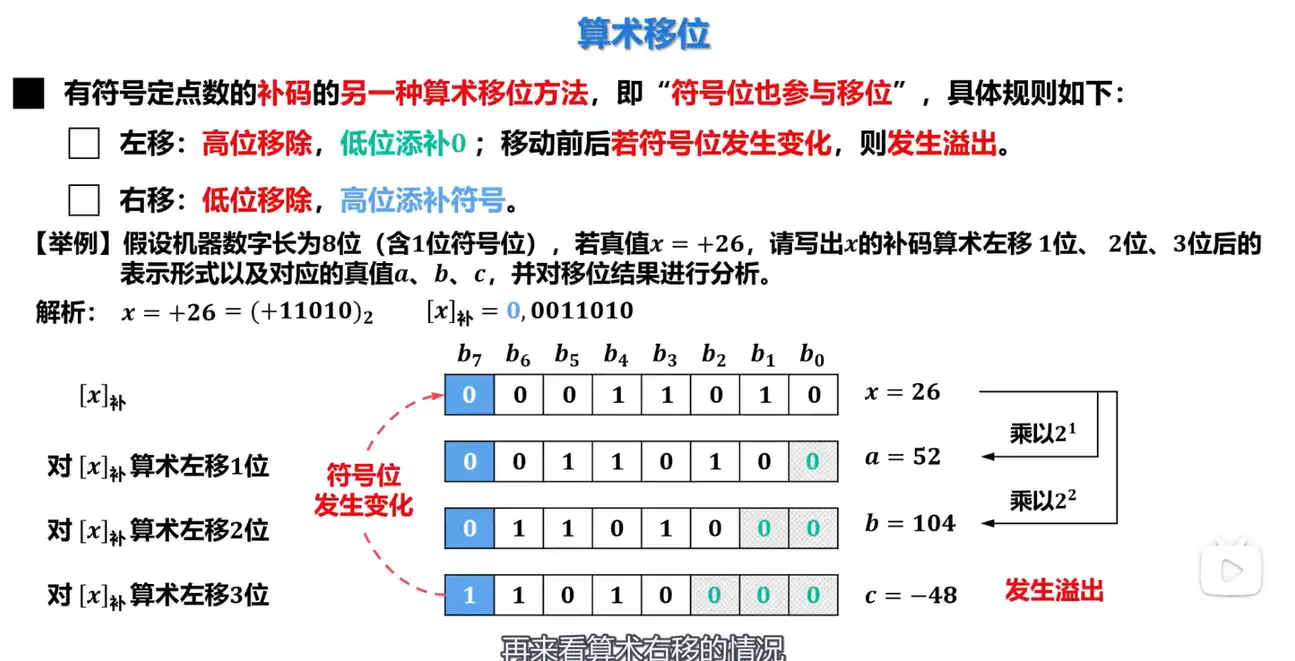
- 符号位也参与移位。
- 左移:高位移除,低位补零,若符号发生变化,则发生溢出。
- 右移:低位移除,高位填补符号位。

Q: 补码的符号位也参与移位的移位方法的优点是什么?
A: - 能够检测出溢出。
- 符号位与数值位一起移位,方便 ALU 处理。
- 填补规则更容易记忆。
C 语言中的移位运算符
Q: C 语言中的移位运算符有哪些?
A: 
<<: 左移运算符。>>: 右移运算符。
Q: C 语言中移位运算符如何对应汇编指令?
A: 
- 左移运算符对应汇编指令中的逻辑左移,也就是高位移除,低位补0。
- 右移运算符根据操作数是无符号数还是有符号数,分别对应汇编指令中的逻辑右移和算术右移。
计算机组成原理微课堂 - 循环移位运算
循环移位运算的定义
Q: 循环移位运算是什么?
A: 循环移位运算是指将无符号数二进制形式中的各个位向左或向右移动,被移出的位会重新出现在另一端形成循环。
循环移位运算的分类
Q: 循环移位运算可以分为哪几种?
A: 循环移位运算可以分为四种:
- 不带 CF 标志位的循环右移
- 不带 CF 标志位的循环左移
- 带 CF 标志位的循环右移
- 带 CF 标志位的循环左移
Q: CF 标志位是什么?
A: CF 标志位用于标识在执行算术或逻辑操作时是否发生了进位。
不带 CF 标志位的循环移位
Q: 不带 CF 标志位的循环右移的规则是什么?
A: 寄存器各位存储的二进制数同时向右移动,从最低位移出的二进制数会被移入到最高位,并存入 CF 标志位。
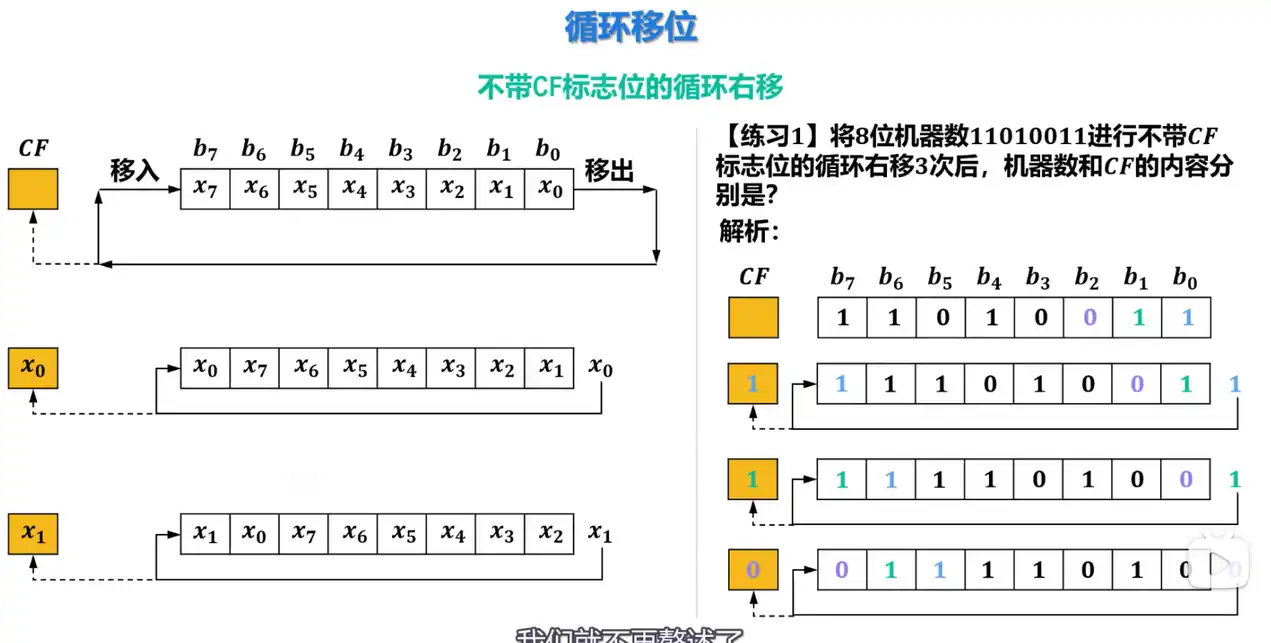
Q: 不带 CF 标志位的循环左移的规则是什么?
A: 寄存器各位存储的二进制数同时向左移动,从最高位移出的二进制数会被移入到最低位,并存入 CF 标志位。
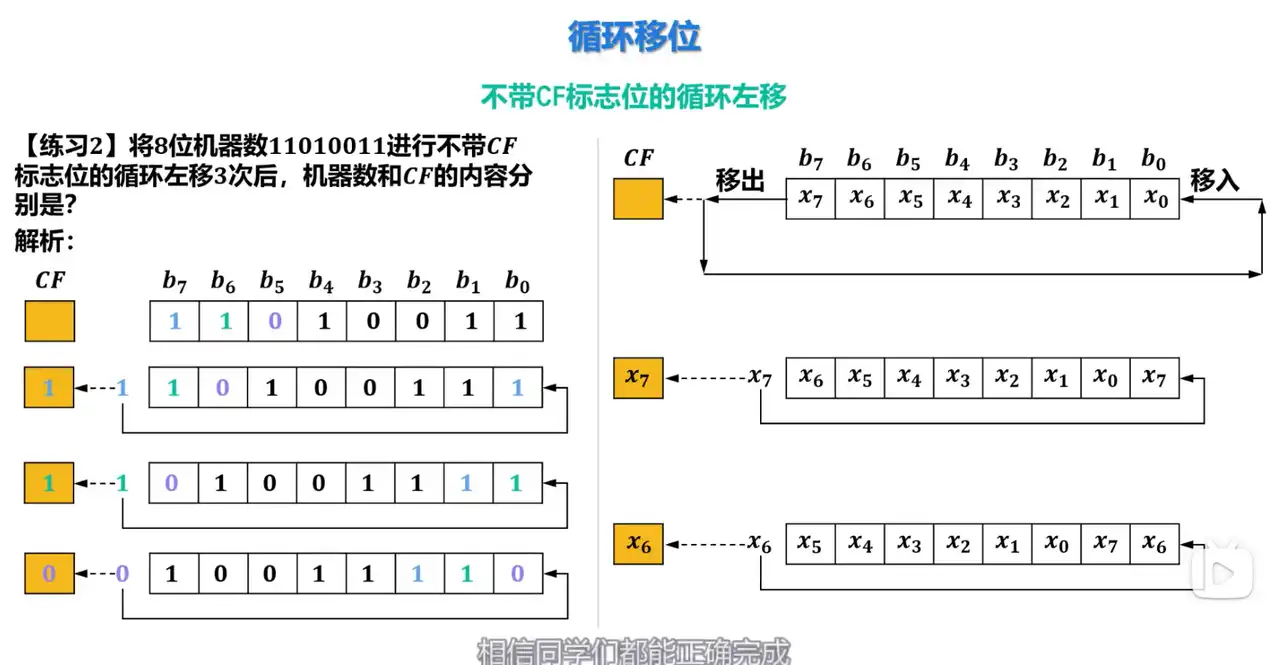
带 CF 标志位的循环移位
Q: 带 CF 标志位的循环右移的规则是什么?
A: CF 标志位存储的二进制数和寄存器各位存储的二进制数同时向右移动,从 CF 标志位移出的二进制数会被移入到寄存器的最高位,而从寄存器最低位移出的二进制数会被移入到 CF 标志位。
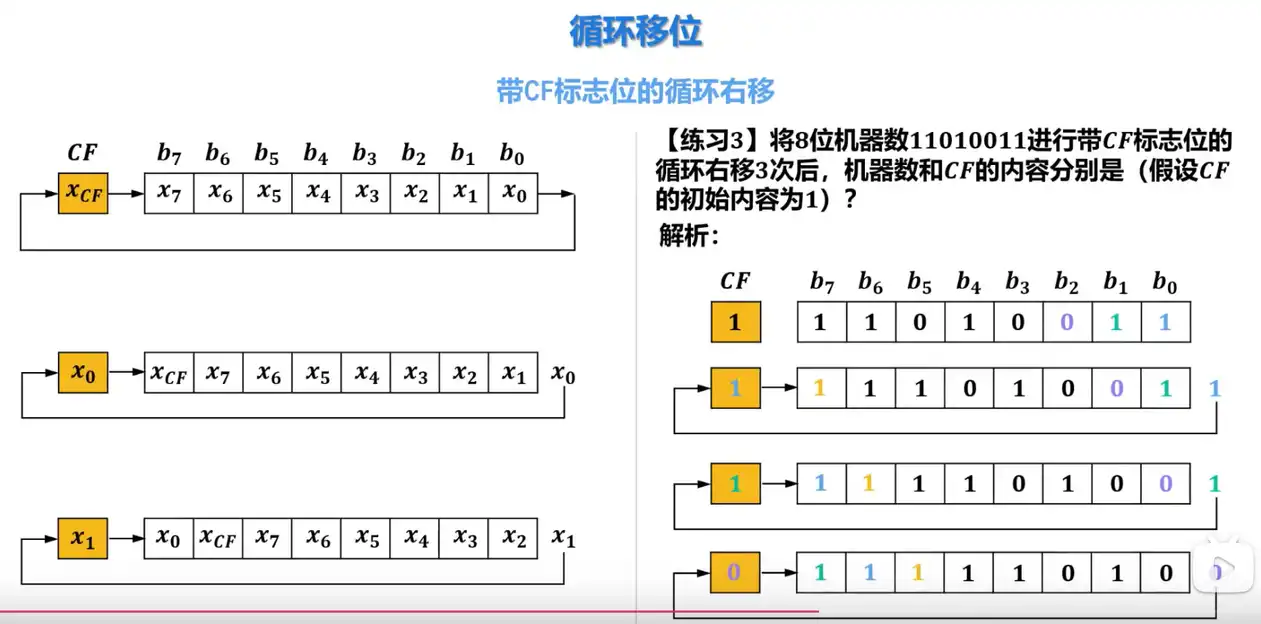
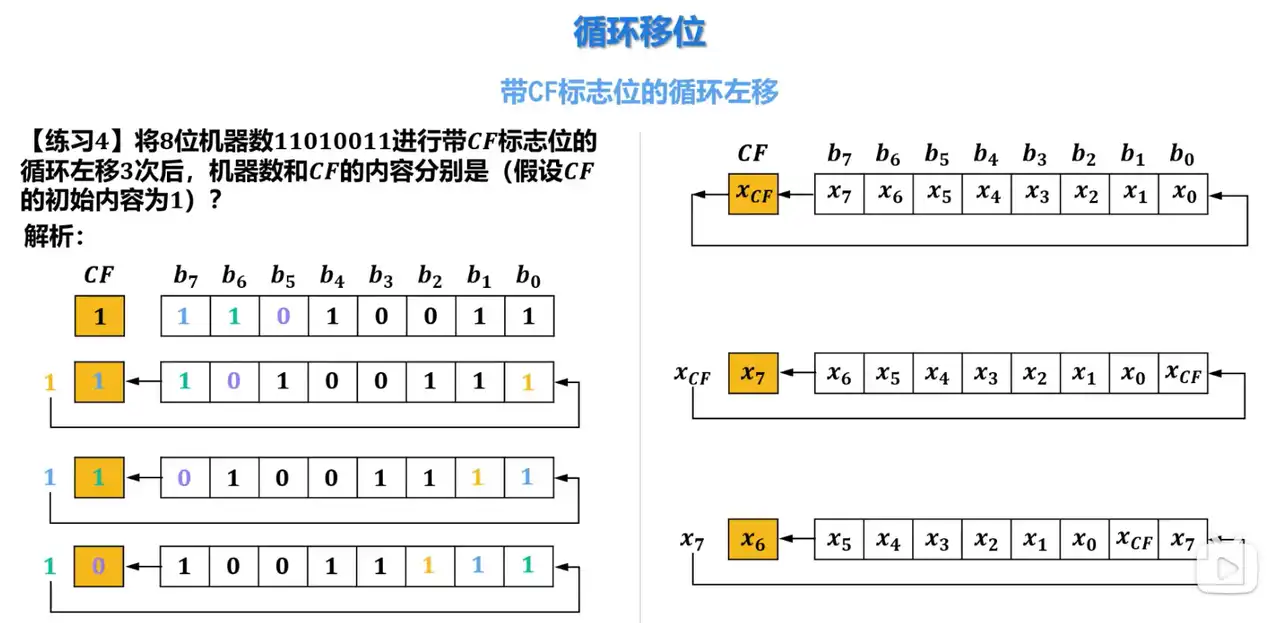
Q: 带 CF 标志位的循环左移的规则是什么?
A: CF 标志位存储的二进制数和寄存器各位存储的二进制数同时向左移动,从寄存器的最高位移出的二进制数会被移入到 CF 标志位,而从 CF 标志位移出的二进制数会被移入到寄存器的最低位。
循环移位运算的应用
Q: 循环移位运算有哪些应用?
A:
- 加密算法:实现数据的混淆和置换,增强加密算法的安全性。
- 哈希函数:改变输入数据的排列顺序,产生不同的哈希值,增强哈希函数的混淆性和扩散性。
- 优化算法:加速算法的执行,节省资源。
C 语言中的循环移位运算
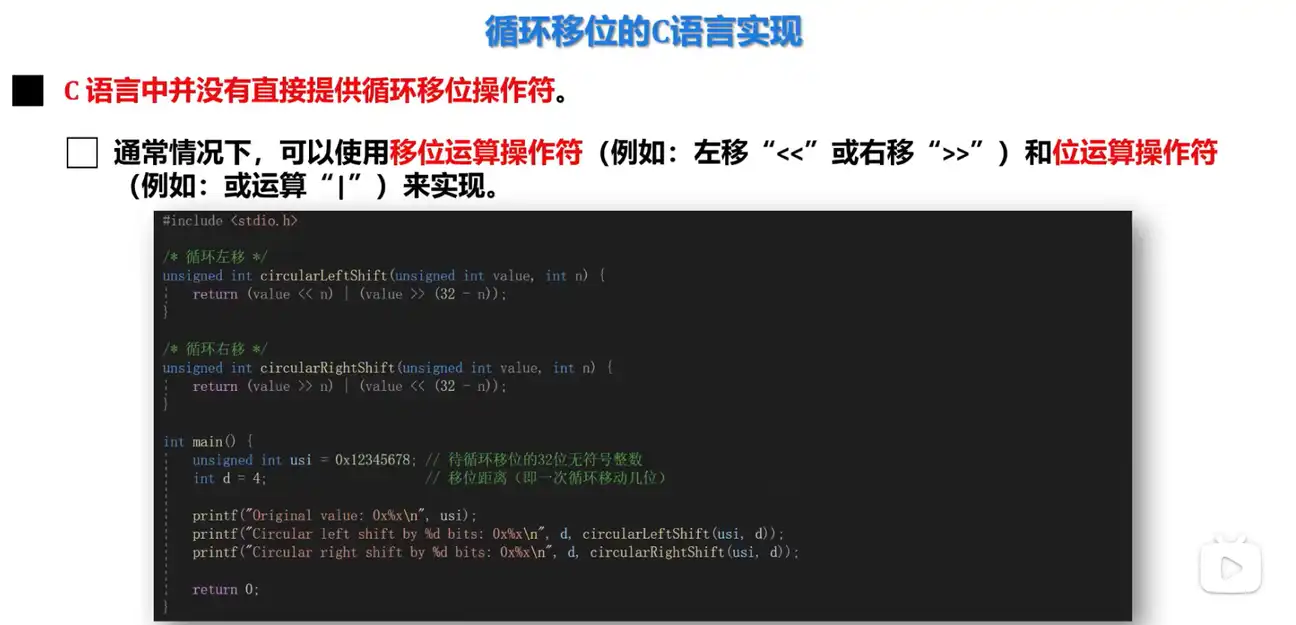
Q: C 语言中如何实现循环移位运算?
A: C 语言中可以使用移位运算操作符和位运算操作符来实现循环移位运算。
计算机组成原理微课堂 - 补码加减法运算公式
补码加减法运算公式
Q: 补码加法运算公式是什么?
A: 两数补码的和等于两数和(真值原码的和)的补码。

Q: 补码减法运算公式是什么?
A: 两数补码的差等于两数差(真值原码的差)的补码。

计算机组成原理微课堂 - 补码加减法运算的溢出检测
溢出的概念
Q: 溢出是什么?
A: 溢出是指当运算结果超出计算机所能表示的数据范围时发生的现象。
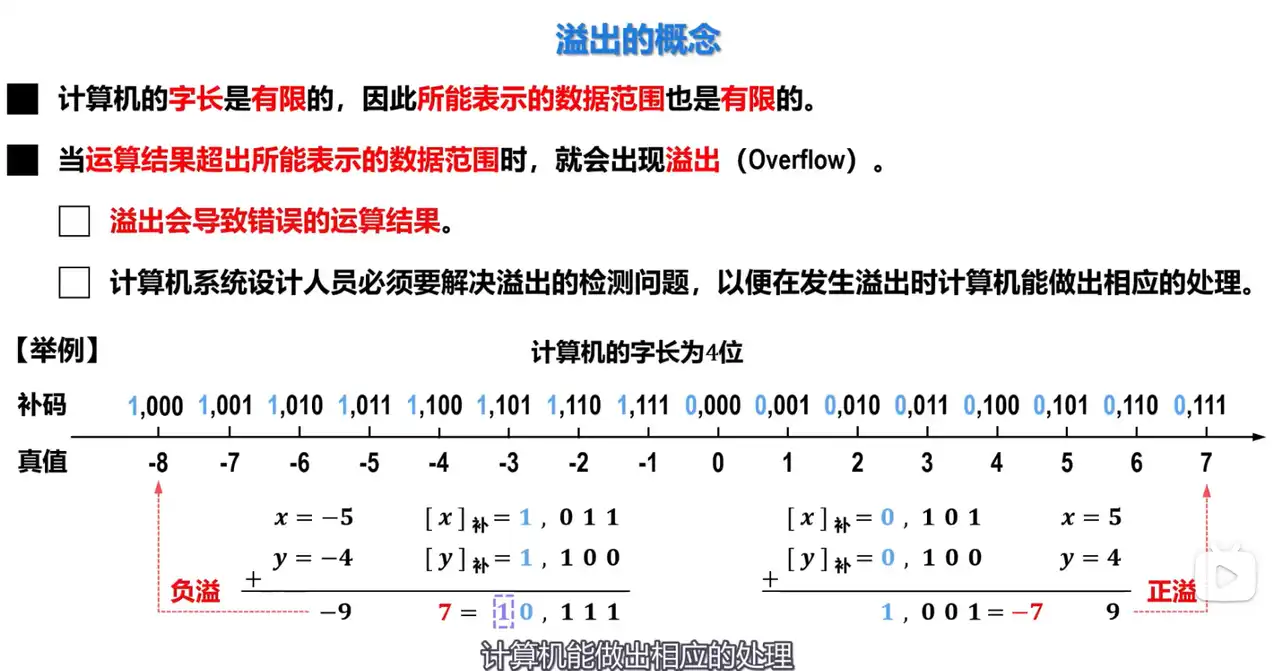
Q: 溢出会导致什么问题?
A: 溢出会导致错误的运算结果。

补码加减法运算的溢出检测方法
Q: 补码加减法运算的溢出检测方法有哪些?
A:
- 方法一:根据操作数的符号位与运算结果的符号位是否一致进行判断。
- 方法二:根据运算过程中最高数值位的进位与符号位的进位是否一致进行判断。
- 方法三:利用变形补码的符号位进行判断。
方法一:符号位比较
Q: 补码加减法运算的溢出检测方法中的方法一”根据操作数的符号位与运算结果的符号位是否一致进行判断”的规则是什么?
A: 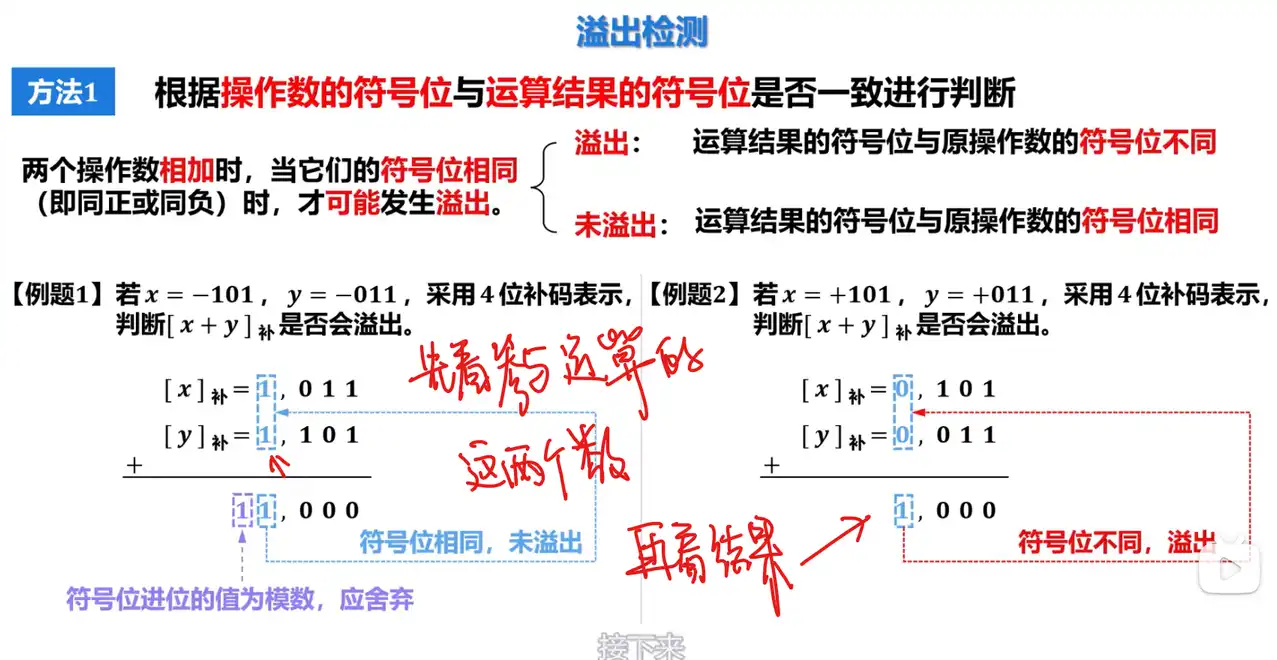
- 两个操作数相加时,当它们的符号位相同(同正或同负)时才可能发生溢出。
- 若运算结果的符号位与原操作数的符号位不同,则发生溢出。
- 若运算结果的符号位与原操作数的符号位相同,则未发生溢出。
由于采用补码可将减法运算转换成加法运算,因此不论作加法还是减法,只要实际参加运算的两个操作数符号相同,但运算结果的符号位与原操数不同,即为溢出。
方法二:进位比较
Q: 补码加减法运算的溢出检测方法中的方法二:根据运算过程中最高数值位的进位与符号位的进位是否一致进行判断的规则是什么?
A:
- 若运算过程中最高数值位的进位与符号位的进位不相同,则可判定为产生溢出。
- 若相同,则可判定为没有产生溢出。
方法三:变形补码
Q: 补码加减法运算的溢出检测方法中的方法三:利用变形补码的符号位进行判断的规则是什么?
A: 
- 变形补码具有两个符号位。
- 双符号位为 00 时表示正数。
- 双符号位为 11 时表示负数。
- 双符号位为 01 时表示正溢出。
- 双符号位为 10 时表示负溢出。
符号位写两遍
计算机组成原理微课堂 - 逻辑代数和逻辑门
逻辑代数
Q: 逻辑代数中的逻辑运算可以分为哪两大类?
A: 逻辑代数中的逻辑运算可以分为基本逻辑运算和复合逻辑运算两大类。
Q: 基本逻辑运算有哪些?
A: 基本逻辑运算包括与运算、或运算、非运算。
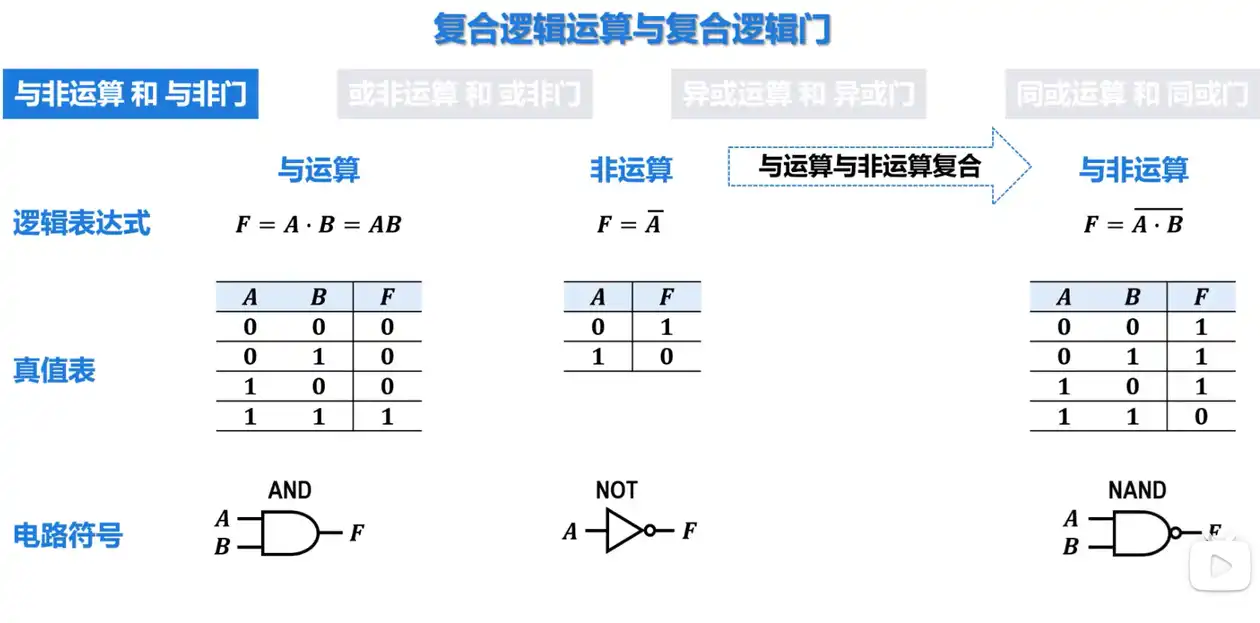
Q: 复合逻辑运算有哪些?
A: 复合逻辑运算包括与非运算、或非运算、异或运算、同或运算。
与运算和与门
Q: 与运算的规则是什么?
A: 只有输入都为真时,输出才为真。
或运算和或门
Q: 或运算的规则是什么?
A: 只要输入有一个为真,输出就为真。
有一个1就是1
复合逻辑运算和复合逻辑门
Q: 异或运算的规则是什么?
A: 两个输入只要不同,输出即为真。
Q: 同或运算的规则是什么?
A: 两个输入相同,输出为真。
计算机组成原理微课堂 - 运算器
运算器的分类
Q: 运算器可以分为哪两种?
A: 运算器可以分为定点运算器和浮点运算器。
定点运算器
Q: 定点运算器的核心是什么?
A: 定点运算器的核心是算术逻辑单元 ALU (Arithmetic Logic Unit)。
浮点运算器
Q: 浮点运算器的核心是什么?
A: 浮点运算器的核心是浮点运算单元 FPU (Floating-Point Unit)。
Q: FPU 可以进行哪些运算?
A: FPU 可以进行浮点数的算术运算。
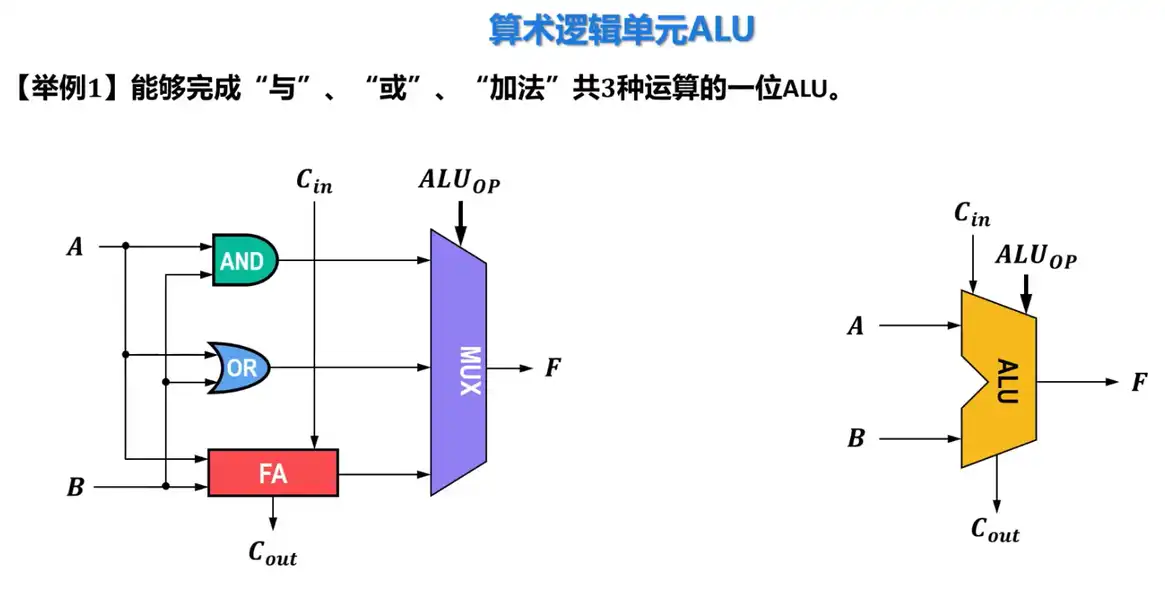
一位 ALU 的实现
Q: 一位 ALU 的重要组成部分是什么?
A: 一位 ALU 的重要组成部分是与门、或门、一位全加器和多路选择器。

Q: 多路选择器的作用是什么?
A: 多路选择器用于选择输出运算结果。
N 位 ALU 的实现
Q: 如何用 N 个一位 ALU 来构建 N 位 ALU?
A: 将各 ALU 内部的一位全加器按照串行进位加法器进行连接。
ALU 的输出
Q: ALU 的输出除了运算结果外,还包括什么?
A: ALU 的输出除了运算结果外,还包括若干状态标志位,例如:
- 零标志位 (ZF)
- 溢出标志位 (OF)
- 符号标志位 (SF)
- 进位标志位 (CF)

状态寄存器
状态寄存器(x86)用于存储 ALU 的状态标志位,为后续指令提供执行依据。
定点运算器的组成
Q: 定点运算器的组成除了 ALU 外,还包括什么?
A: 定点运算器的组成除了 ALU 外,还包括通用寄存器组、缓冲寄存器等功能部件,它们之间使用内部总线进行连接。
2. 什么称为无符号整数的 “溢出”?
Q: 无符号整数的“溢出”是什么?
A: 无符号整数的“溢出”是指当运算结果超出了计算机所能表达的范围,有效数值进到了第 n+1 位时发生的现象。
对于无符号定点整数来说,若寄存器位数不够,则计算机运算过程中一般保留低 n 位,舍弃高位。这样, 会产生以下两种结果
- 保留的低 n 位数不能正确表示运算结果。在这种情况下,意味着运算的结果超出了计算机所能表达的范围,有效数值进到了第 n+1 位,称此时发生了 “溢出” 现象。
- 保留的低 n 位数能正确表达计算结果,即高位的舍去并不影响其运算结果。
Q: 如何判断一个浮点数是否是规格化数?
A: 对于原码编码的尾数,只要看尾数的第一位是否为 1 就行。需要注意的是, IEEE 754 标准的浮点数尾数是用原码编码的
对于补码表示的尾数,只要看符号位和尾数最高位是否相反。
4. 对于位数相同的定点数和浮点数, 可表示的浮点数个数比定点数个数多吗?
Q: 对于位数相同的定点数和浮点数,可表示的浮点数个数比定点数个数多吗?
A: 不是,可表示的数据个数取决于编码所采用的位数。编码位数一定,编码出来的数据个数就是一定的。
Q: n 位编码可以表示多少个数?
A: n 位编码可以表示 2^n 个数。
5. 现代计算机中是否要考虑原码加减运算? 如何实现?
Q: 现代计算机中是否要考虑原码加减运算?
A: 是的,现代计算机中的浮点数采用 IEEE 754 标准,所以进行两个浮点数的加减运算时,必须考虑原码的加减运算,因为 IEEE 754 标准的浮点数尾数都采用原码表示。
Q: 原码的加减运算如何实现?
A: 1. 转换为补码后,用补码加减法实现,结果再转换为原码。
2. 直接用原码进行加减运算,符号位和数值位分开处理。