2.3.2 浮点数的加减运算
1. 对阶
Q: 对阶的目的是什么?
A: 对阶的目的是使两个操作数的小数点位置对齐,即使得两个数的阶码相等。
Q: 对阶的步骤是什么?
A: 1. 求阶码差。
2. 以小阶码向大阶码看齐的原则,将阶码小的尾数右移一位,阶码加 1,直到两个数的阶码相等为止。
Q: 对阶时需要注意什么?
A: - 尾数右移时,低位移出的位不要丢掉,应保留并参加尾数部分的运算。
- 不能采用大阶码向小阶码看齐的原则,因为会导致最高有效位被移出,结果出错。
2. 尾数加减
Q: 尾数加减如何进行?
A: 将对阶后的尾数按定点原码小数的加 (减) 运算规则进行运算。
Q: 尾数加减时需要注意什么?
A: - 必须将隐藏位还原到尾数部分。
- 运算后的尾数不一定是规格化的,需要进行规格化处理。
3. 尾数规格化
Q: 尾数规格化的目的是什么?
A: 使尾数符合 IEEE 754 规格化尾数的形式,即 ±1.xxx...x。
Q: 尾数规格化的步骤是什么?
A: - 右规:当结果为 ±1.xxx...x 时,尾数右移一位,阶码加 1。
- 左规:当结果为
±0.0...01xxx...x时,尾数每左移一位,阶码减 1,直到将第一位 1 移到小数点左边。
Q: 尾数规格化需要注意什么?
A: - 左规一次相当于乘以 2,右规一次相当于除以 2。
- 需要右规时,只需进行一次。
4. 舍入
Q: 舍入的目的是什么?
A: 保证运算精度,将运算结果还原成 IEEE 754 格式。
Q: IEEE 754 提供了哪些舍入模式?
A: - 就近舍入:舍入为最近的可表示数。
- 正向舍入:朝数轴 +∞ 方向舍入。
- 负向舍入:朝数轴 -∞ 方向舍入。
- 截断法:直接截取所需位数,丢弃后面的所有位。
5. 溢出判断
Q: 浮点数运算时如何判断溢出?
A: - 指数上溢:当一个正指数超过了最大允许值时,发生指数上溢。
- 指数下溢:当一个负指数超过了最小允许值时,发生指数下溢。
Q: 溢出判断需要注意什么?
A: - 尾数溢出可以通过右规操作得到纠正。
- 运算结果是否溢出主要看结果的指数是否发生了上溢。
总结
Q: 浮点数加减运算需要注意哪些问题?
A: - 对阶时要保留低位移出的位。
- 尾数加减时要还原隐藏位。
- 尾数规格化时要进行左规或右规。
- 舍入时要选择合适的舍入模式。
- 溢出判断时要关注指数是否发生了上溢。
2.3.4 数据的大小端和对齐存储
1. 数据的 “大端方式” 和 “小端方式” 存储
Q: 数据的 “大端方式” 和 “小端方式” 存储分别是什么?
A:
- 大端方式 (big endian):先存储高位字节,后存储低位字节。
- 小端方式 (little endian):先存储低位字节,后存储高位字节。
Q: 如何判断一个系统采用的是大端方式还是小端方式?
A: 可以通过检查底层机器级代码来判断。
Q: 小端方式存储的机器代码如何阅读?
A: 小端方式存储的机器代码中,字节是按相反顺序显示的。
2. 数据按 “边界对齐” 方式存储
Q: 数据按 “边界对齐” 方式存储的规则是什么?
A: 
- 每个成员按其类型的大小对齐,
char型的对齐值为 1,short型的对齐值为 2,int型的对齐值为 4,单位为字节。 - 结构体的长度必须是成员中最大对齐值的整数倍。
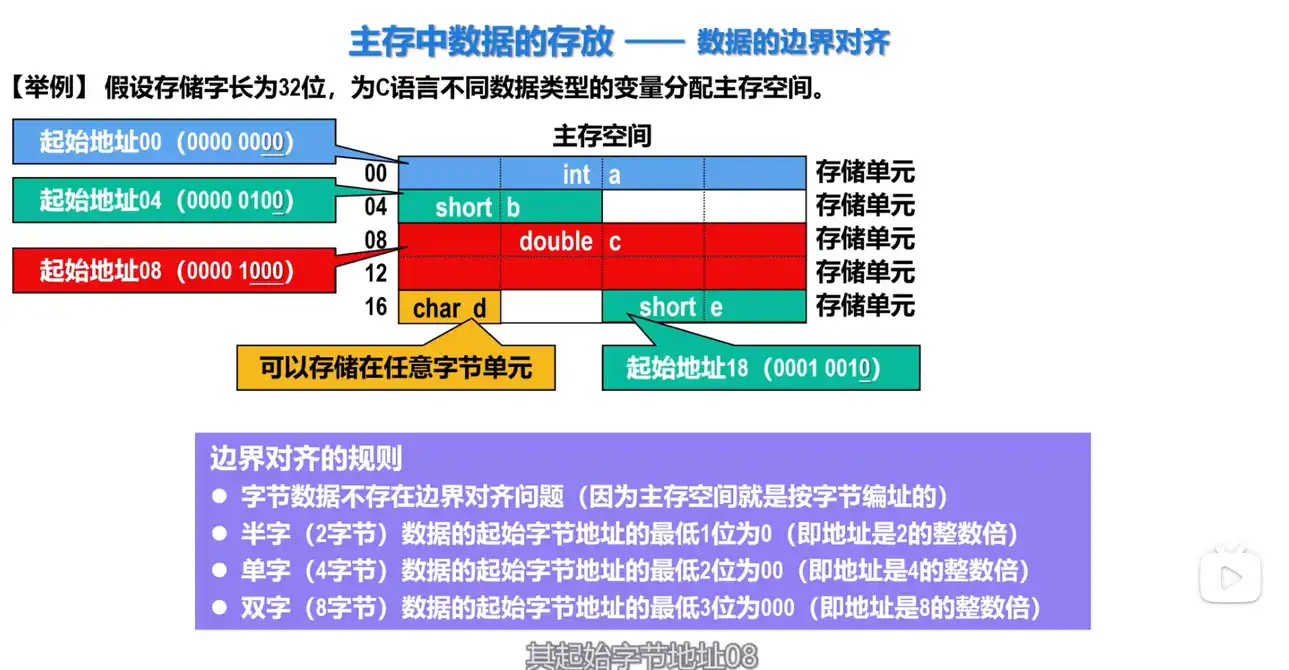
Q: 数据按 “边界对齐” 方式存储的优点是什么?
A: - 提高存取数据的速度。
- 能够适应指令流水。
Q: 数据按 “边界对齐” 方式存储的缺点是什么?
A: 会浪费一些存储空间。
C 语言中的结构体对齐
Q: C 语言中结构体对齐的规则是什么?
A: 
- 每个成员存储的“起始地址 % 该成员的长度 = 0”。
- 结构体的长度也必须是最大成员长度的整数倍。