题168
题目
Q:设
(1) 若
(2) 若
(3) 若
(4) 若
分析
A:24考研数学-矩阵行满秩与列满秩概念题(答疑168)

这里涉及矩阵的秩中一个非常重要的不等式,也叫西尔维斯特不等式:
解

- 如果你是行满秩的话, 那么你这样一个非齐次线性方程组一定有解
- 因为系数矩阵的秩一定是小于等于它的增广矩阵的秩
- 现在我们把它的形状写出来, 你是
, 那么增广矩阵依然是 行 列 - 现在我们知道啥了, 这个矩阵的秩就等于你的行数
- 那么你的增广矩阵的秩也不会超过你的行数呀
- 是不是马上我们就可以得到, A的秩和增广矩阵的秩是相等的
- 当然一定有解
- 如果一个矩阵是列满秩, 那么他说A在前, B在后的这样一个矩阵的乘积的秩就和B的秩一样
- 这个证明方法有两种
- 第一个证明方法是, 证明这样一个齐次线性方程组
, 与这样一个齐次线性方程组 同解啊 - 很好证明, 我们同学可以试一下, 如果咱俩同行了, 咱们的未知数的个数都一样, 所以咱俩的系数矩阵的秩就相当
- 第二个方法, 第二个方法呢, 可以用Sylvester不等式来简单的证明
- 你说A乘B的秩一定是大于等于A的秩, 加B的秩, 再减上一个A乘B的那个相邻下标就是
- 你现在又说了, A的秩就等于它的列数
- 所以A的秩减
就等于零, 那么就等于B的秩 - 一方面A乘B的秩大于等于B的秩
- 还有一方面矩阵越乘秩越小, 你这个矩阵的秩一定是小于等于B的秩
- 这边是B的秩, 这边是B的秩, 是不是可以得到A乘B的秩就等于B的秩
- 第一个证明方法是, 证明这样一个齐次线性方程组
- 这个证明方法有两种
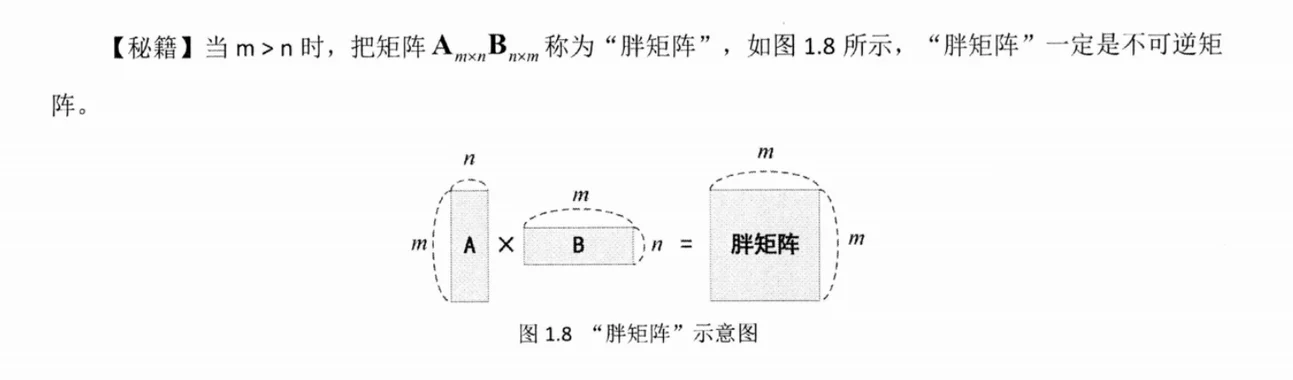
- 胖矩阵一定是不可逆矩阵
- 什么是胖矩阵啊, 就是一个瘦高个乘上一个矮胖子, 乘出来一个大大的方方的一个方阵
- 那么这样一个矩阵我把它叫胖矩阵
- 比如你是三行乘一列, 我是一行乘三列乘, 从来是一个三阶方阵
- 那么这样的矩阵一定是不可逆矩阵的
- 我们来看第二个选择, A是A的秩是
就是列满秩, 那么我们这里头就考虑方程组, 所以我们就想把这个等式转置一下, 看能不能证明, 看能不能够证明, 乘 一定等于一个单位矩阵 , 一能不能证明呢 - 那你刚刚说了, A是列满秩, 那么是不是A的转置就等于A的行数, 就是行满秩
- 这个矩阵行满秩, 那么当然这个方程组随便右边随便写, 谁都一定有解
- 那我写的是啥呢, 就写的这个单位矩阵的
个列向量, 这个就是 就是一到 - 那么这个方程组总是有解的, 那是不是就存在一个
就等于 - 你知道
就等于 - 把这
个等式与合并, 是不是就有 乘上一个矩阵, 我把这个矩阵叫 , 就等于等于 - 再一转置回来, 是不是就可以证出你这样一个结论, 所以二选项是正确的
- 那么四选项就是我们刚刚说的A是列满秩, 那么A在前, B在后, 这样一个矩阵的秩就等于B的秩
- 那么怎么样来证明三呢
- 三我们来看你对这个矩阵做一个转置啊, 也就是
这个矩阵的秩, 当然等于 取上一个转置的秩, 那就等于 乘 - 这个时候我们发现A是行满秩, 转置一下以后, 这个矩阵是不是列满秩了
- 这个矩阵列满秩就可以用刚刚四的结论, 那他就等于
的秩 - 而
的秩当然等于 的秩啊 - 所以我们的234都是正确
- 那么一证明不了, 那就举反例, 怎么举反例
- 我们假设这个A只有一行123
- 你说你是行满秩, 我就一行嘛啊, 非零向量吧, 非零行向量当然是行满秩
- 那么你说你乘出来要个单位矩阵
, 我这是一行乘三列, 所以前面这个矩阵一定是 的矩阵, 才能乘出来三阶方阵 - 好吧, 这不管你是几乘出来, 是不是一个胖矩阵
- 胖矩阵一定是一个不可逆矩阵
- 你说要等于三阶单位矩阵一肯定是不可能的啊
- 所以选项一是错误的
-
若
,则 ;;一定有解,这是因为A矩阵的秩一定小于等于它的增广矩阵的秩, . -
若
,也就是A是列满秩,那么 和 有什么关系;; ,这是通过Sylvester不等式得到的结论, .或者用另一种方法证明, 与 同解,所以 . -
“胖”矩阵一定是;;不可逆方阵.