题116
题目
A 为 m×n 矩阵,B 为 n×m 矩阵,已知任意 m 维列向量为是方程组ABx=0 的解向量,任意非零 2m 维列向量都不是方程组
已知 a 是 Ax=0 的非零解向量,则以下证确的命题有
- 2m≤n
- 方程组 BAx=0 有 n-m 个线性无关解向量。
- 若 2m=n,则
有唯一解。 - 方程组 BAx=0 与 Ax=0 同解。
分析
考察了这些知识点:

-
设任意
维列向量(针对 的描述)是方程组 的解向量,则;; -
设任意非零
维列向量都不是方程组 的解向量,则;; ,也就是说 是列满秩的 -
若
,则 列向量;;线性无关,同时,A的列向量的任意子集,也就是任意一部分,也是线性无关的 -
若
,则;; ( 指 和 相邻下标)。 -
若
与 同解,则;; 。 -
齐次线性方程组中,若
,则;;;矩阵的秩和 只有零解。 -
若
,则 的列向量是;;; 的解向量。 -
若
;;不一定有唯一解,也就是说 是列满秩不一定能推出方程组有唯一解,因为还没有确定增广矩阵的秩 -
要确定非齐次线性方程组
有唯一解,首先要保证;;;方程组有解,即系数矩阵的秩和增广矩阵的秩相等,且等于列数
解

- 证明命题1:
- 任意
维向量都是方程组 的解 , , …, 都是方程组 的解 -
1 & & \
& \ddots & \
& & 1
\end{bmatrix}=0$$,也就是 - 任意2m维列向量(非空)不是方程组
的解,所以方程组 只有零解,也就是 是它的列数 - 矩阵
的秩等于 - 矩阵
的秩等于 - 矩阵
是列满秩,矩阵 的秩也是满秩,等于
- 矩阵
的秩加 的秩小于等于
- 任意
- 证明命题2:方程组
有 个线性无关解向量 - 研究方程组
的基础解系 - 方程组
与 同解 - 方程组
的基础解系含有 个解向量 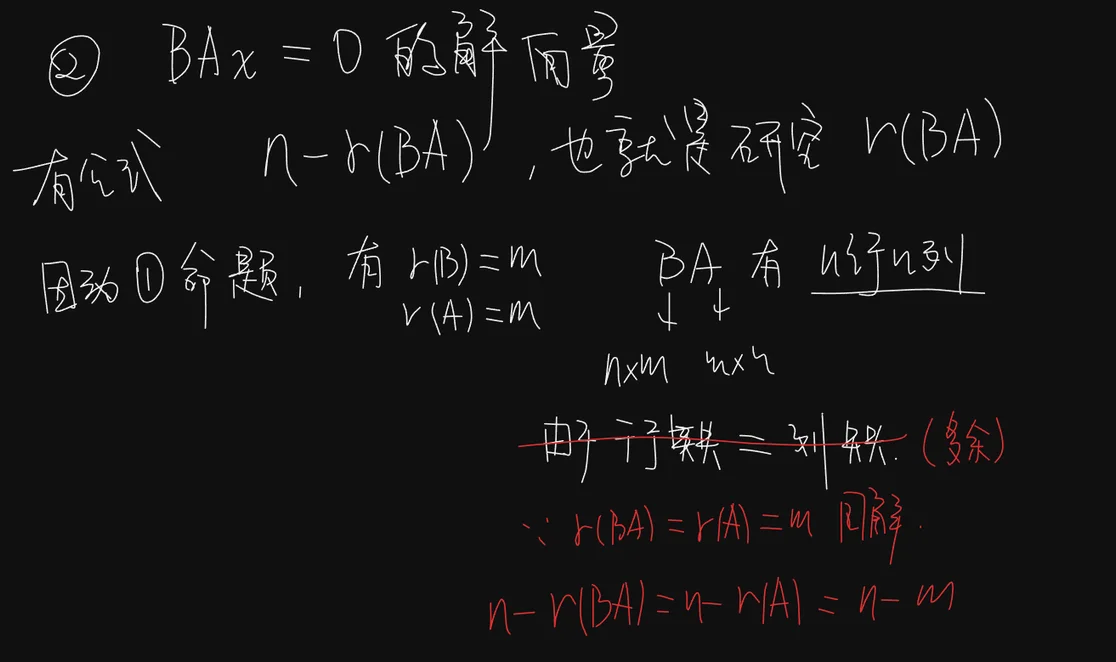
- 研究方程组
- 证明命题3:若
,则 有唯一解 的所有列向量都是方程组 的解向量 - 方程组
的基础解系含有 个线性无关的解向量 - 当
时,方程组 的基础解系含有 个线性无关的解向量 - 矩阵
的所有列向量是方程组 的一个基础解系 是 的解,可以由 线性表示
- 矩阵
- 方程组
有解 - 矩阵
是列满秩 - 方程组
有唯一解
- 证明命题4:方程组
与 同解 - 假设
是方程组 的解 是方程组 的解 - 假设
是方程组 的解 - 矩阵
是列满秩 - 方程组
只有零解 是方程组 的解 - 方程组
与 同解
- 假设