题4
题目
[!question]+
已知数列
(A)
(B)
(C)
(D)
分析
[!NOTE]+
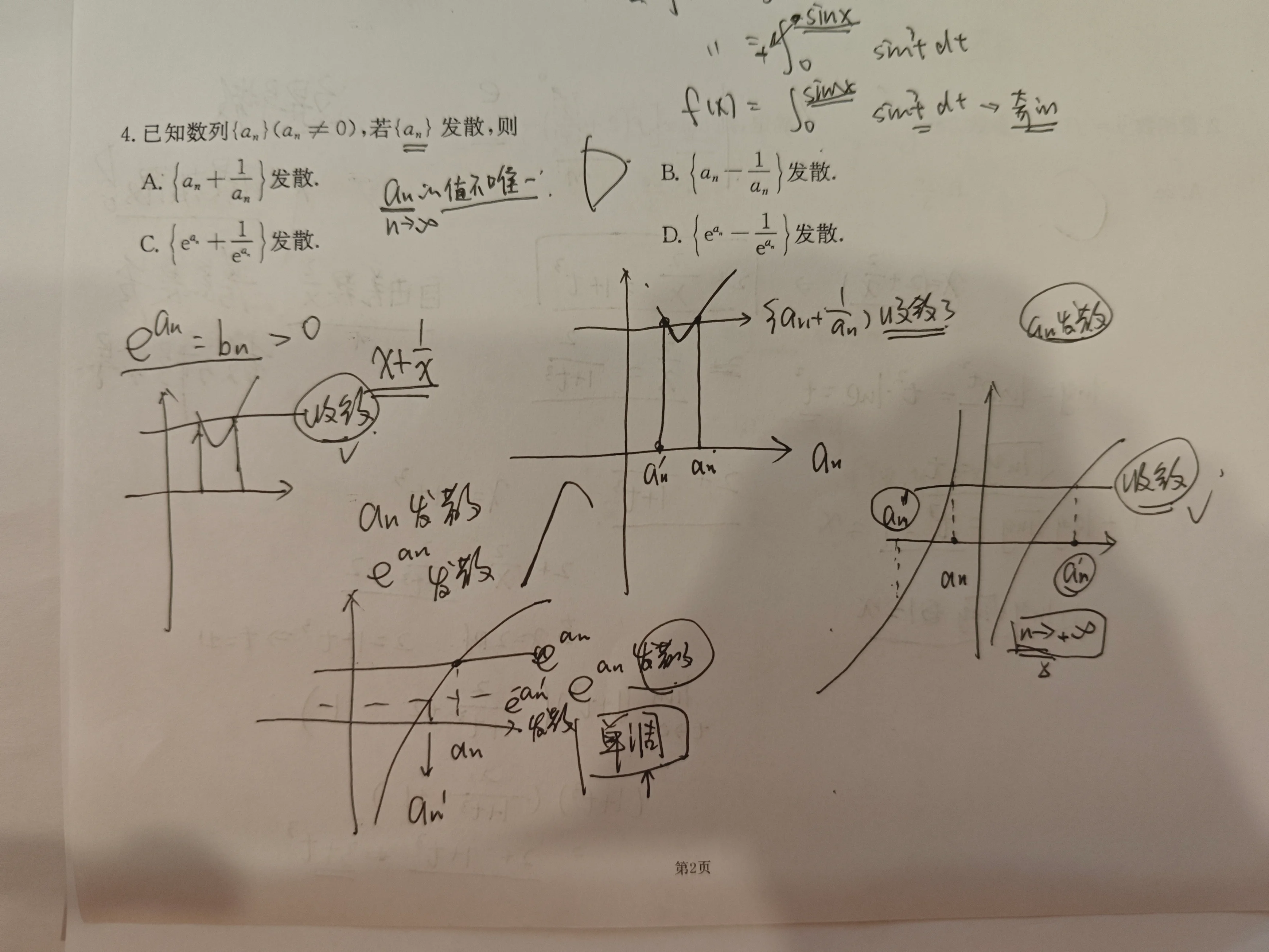
复合函数与数列收敛的题目,核心在于考虑复合函数的单调性和自变量数列之间的对应关系
解
[!done]-
若数列
解:考虑函数
记
若
由此可得,
因此,
下面说明选项 A、B、C 均不正确。
对选项 A,取
对选项 B、C,取
Jun 19, 20252 min read
[!question]+
已知数列
(A)
(B)
(C)
(D)
[!NOTE]+
复合函数与数列收敛的题目,核心在于考虑复合函数的单调性和自变量数列之间的对应关系

[!done]-
若数列
解:考虑函数
记
若
由此可得,
因此,
下面说明选项 A、B、C 均不正确。
对选项 A,取
对选项 B、C,取