题3
题目
已知
(A)
(B)
(C)
(D)
分析
这个题目做错本质上还是又忘记了定积分的定义,从小积到大,我们才能和图形面积的几何意义对应起来:题5。另一方面定积分的定义里面,积分区间上的负号,我们应该用换元的办法把符号换下来,也就是下面的法二
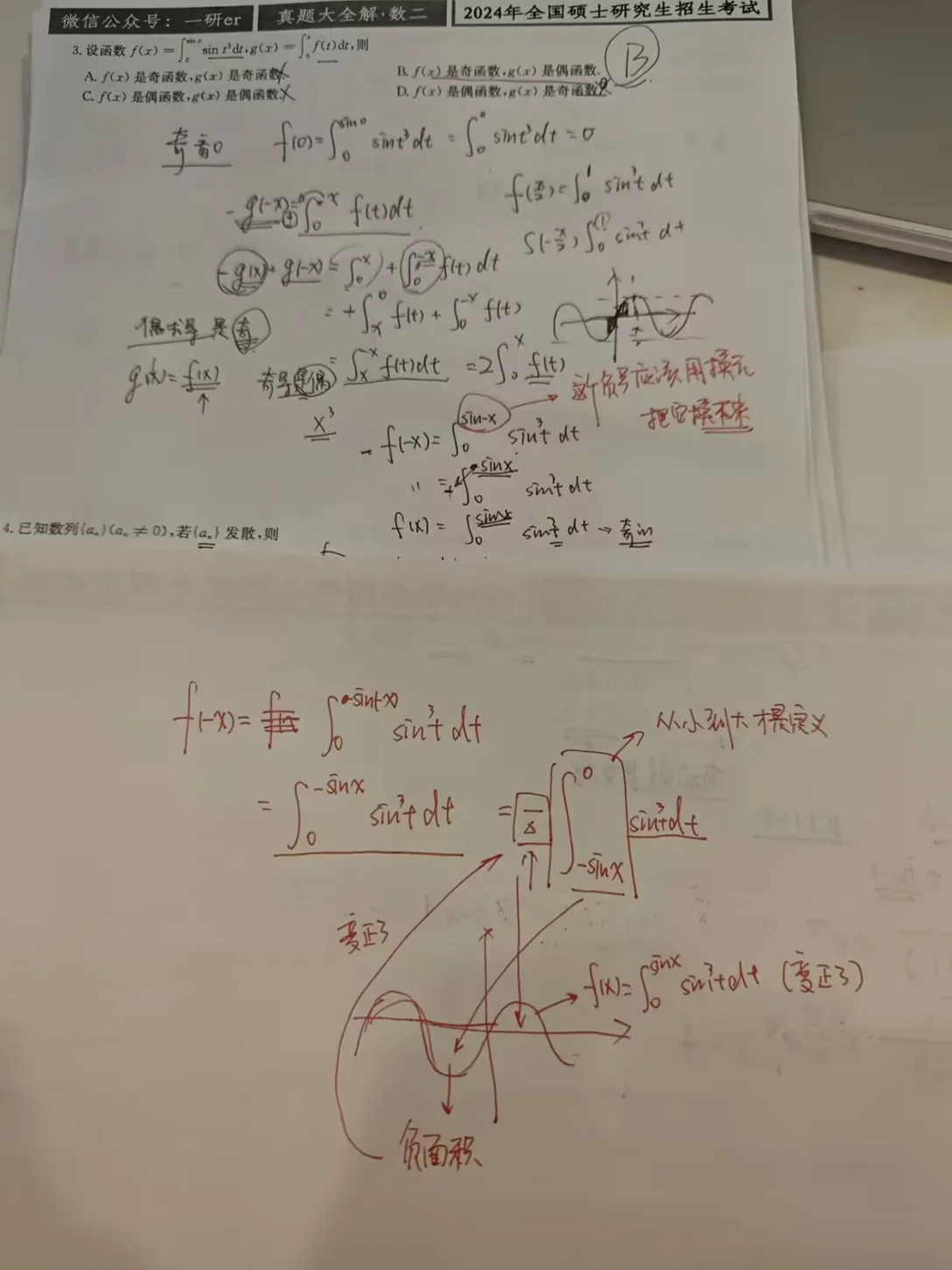
解
若
解 (法一) 由于
于是,
另一方面,
因此,
(法二) 首先考察
于是,
下面考察
于是,
因此,
已知
(A)
(B)
(C)
(D)
这个题目做错本质上还是又忘记了定积分的定义,从小积到大,我们才能和图形面积的几何意义对应起来:题5。另一方面定积分的定义里面,积分区间上的负号,我们应该用换元的办法把符号换下来,也就是下面的法二

若
解 (法一) 由于
于是,
另一方面,
因此,
(法二) 首先考察
于是,
下面考察
于是,
因此,