题20
题目
[!question]+
设平面有界区域
分析
[!NOTE]+
三角函数的积分我们要注意把
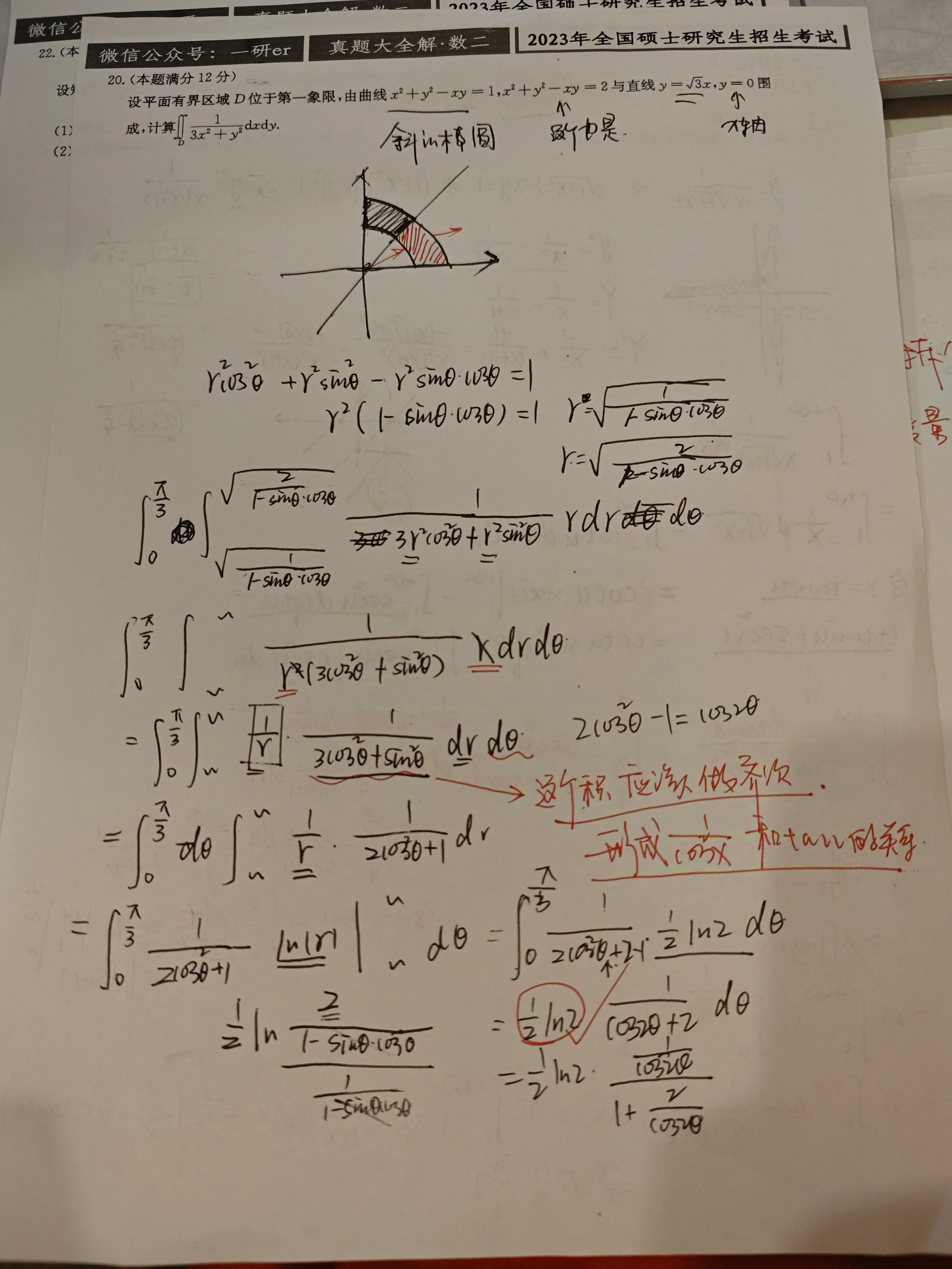
这个题我们也做过:题14.9,强化中也有:例14.17
解
[!done]-
解 在极坐标系下计算.
由
即
因此,
注 ① 由
2,曲线
进一步,令
于是,
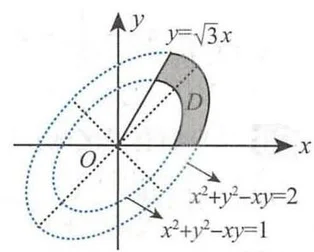
区域
② 也有同学利用二重积分换元法解本题, 但二重积分换元法并不在考试大纲内, 故下面的解法仅供感兴趣的同学参考.
令
由该变换解得
由此可得
Jun 19, 20255 min read
[!question]+
设平面有界区域
[!NOTE]+
三角函数的积分我们要注意把
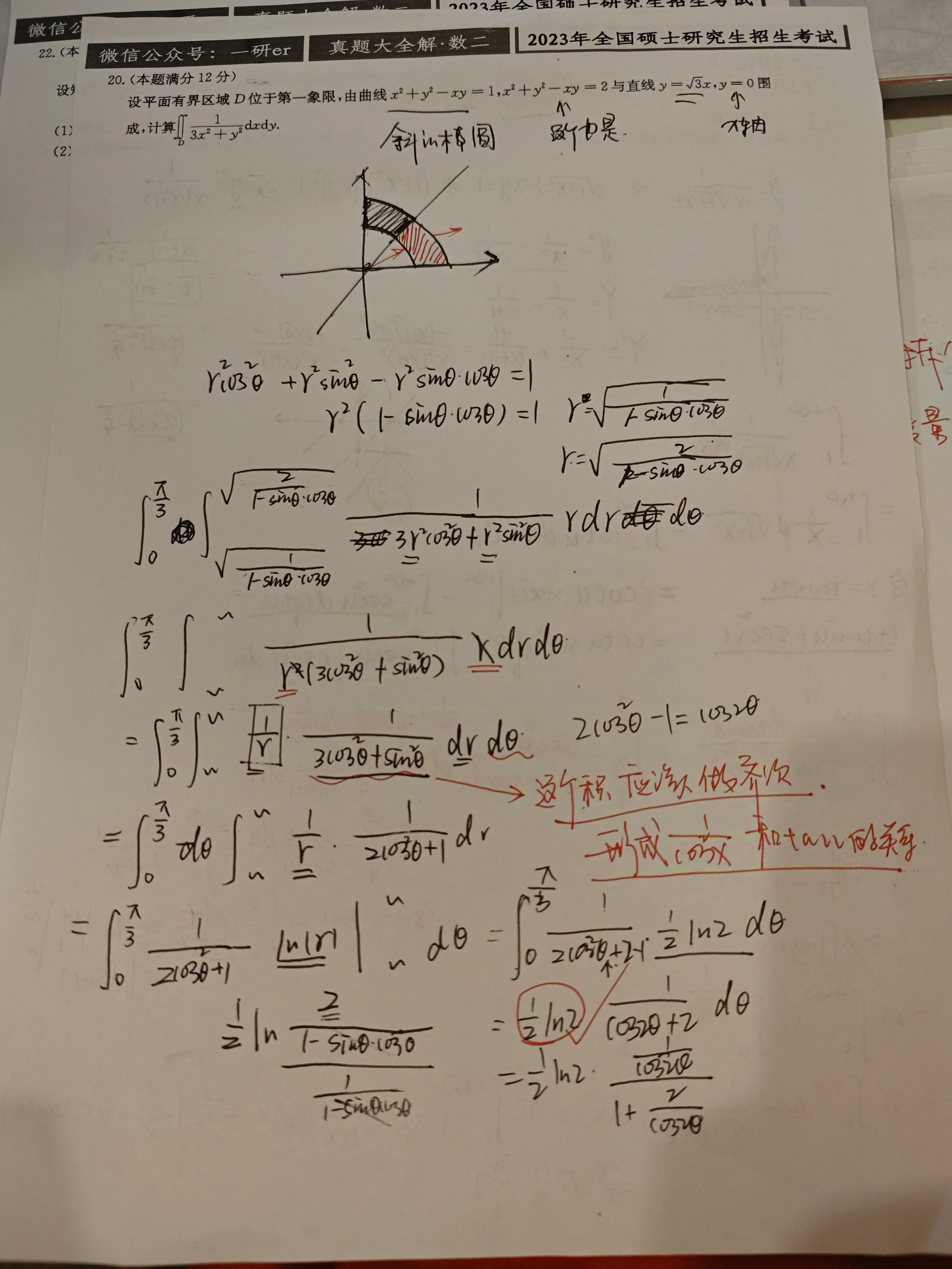
这个题我们也做过:题14.9,强化中也有:例14.17
[!done]-
解 在极坐标系下计算.
由
即
因此,
注 ① 由
2,曲线
进一步,令
于是,

区域
② 也有同学利用二重积分换元法解本题, 但二重积分换元法并不在考试大纲内, 故下面的解法仅供感兴趣的同学参考.
令
由该变换解得
由此可得