题18
题目
[!error]+
求函数
分析
[!NOTE]+
2023 年数学一试题的第 (18) 题也是二元函数的无条件极值问题, 在该题中, 既需要用到二元函数极值存在的充分条件来判定极值, 也需要利用定义来判定极值. 大家可以留作练习:题308
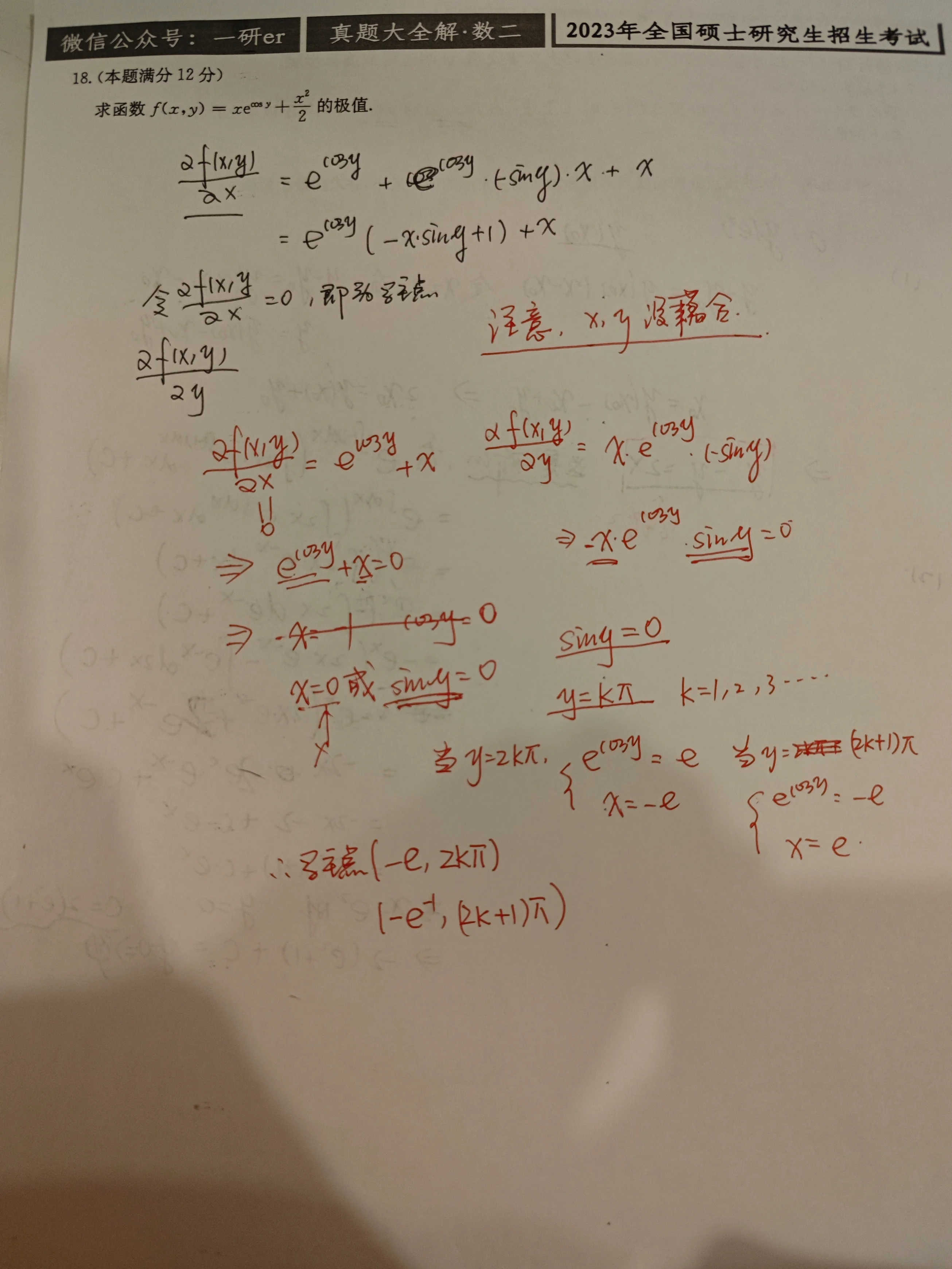
解
[!done]-
解1 计算
令
当
② 计算
③ 计算
(i) 对点
(ii) 对点
综上所述,
[!error]+
求函数
[!NOTE]+
2023 年数学一试题的第 (18) 题也是二元函数的无条件极值问题, 在该题中, 既需要用到二元函数极值存在的充分条件来判定极值, 也需要利用定义来判定极值. 大家可以留作练习:题308
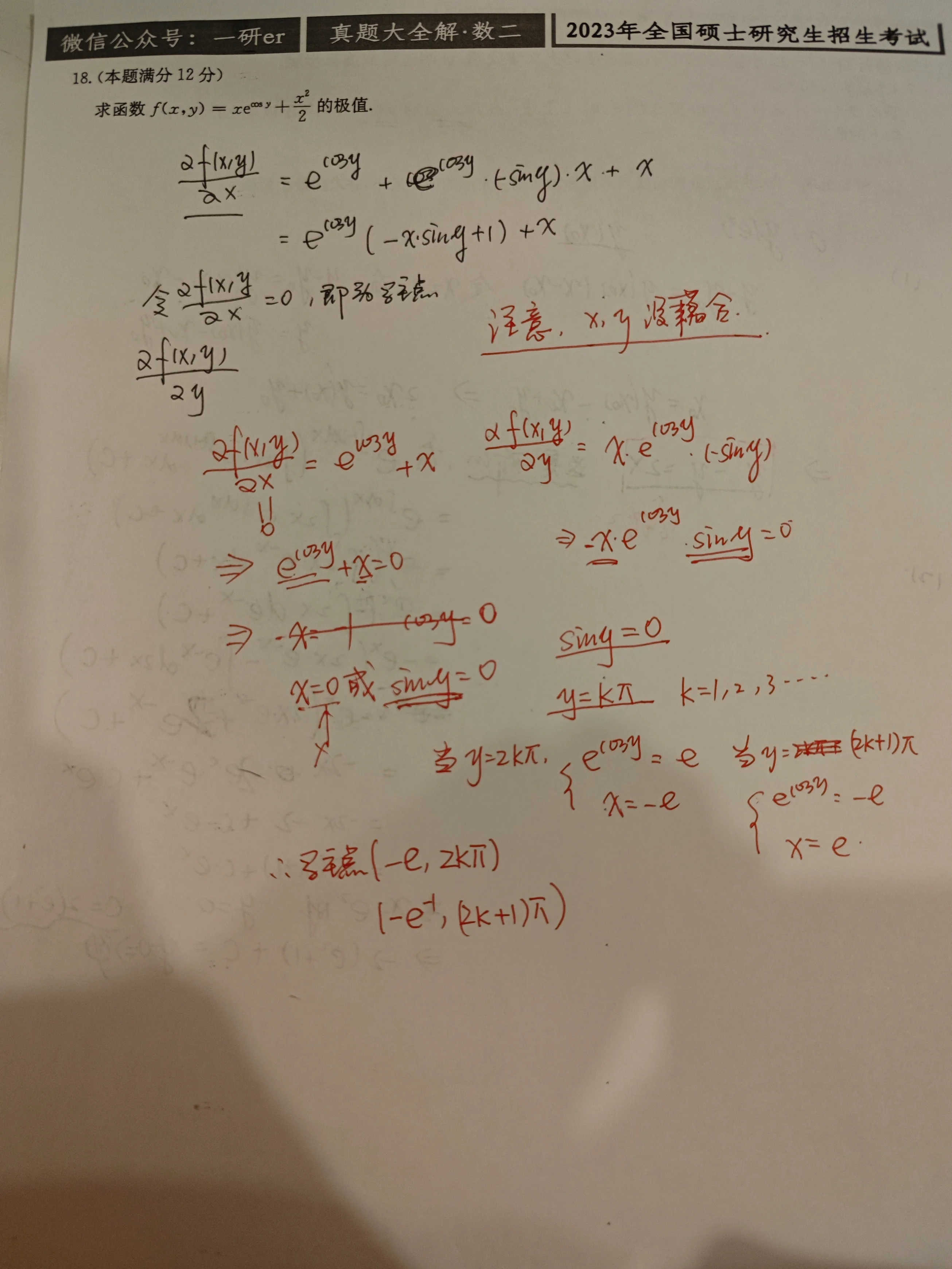
[!done]-
解1 计算
令
当
② 计算
③ 计算
(i) 对点
(ii) 对点
综上所述,