题4
题目
[!question]+
设函数
(A)
(B)
(C)
(D)
分析
[!NOTE]+
这里也是粗心的问题导致算错了,问的是b/a,我算的是a/b
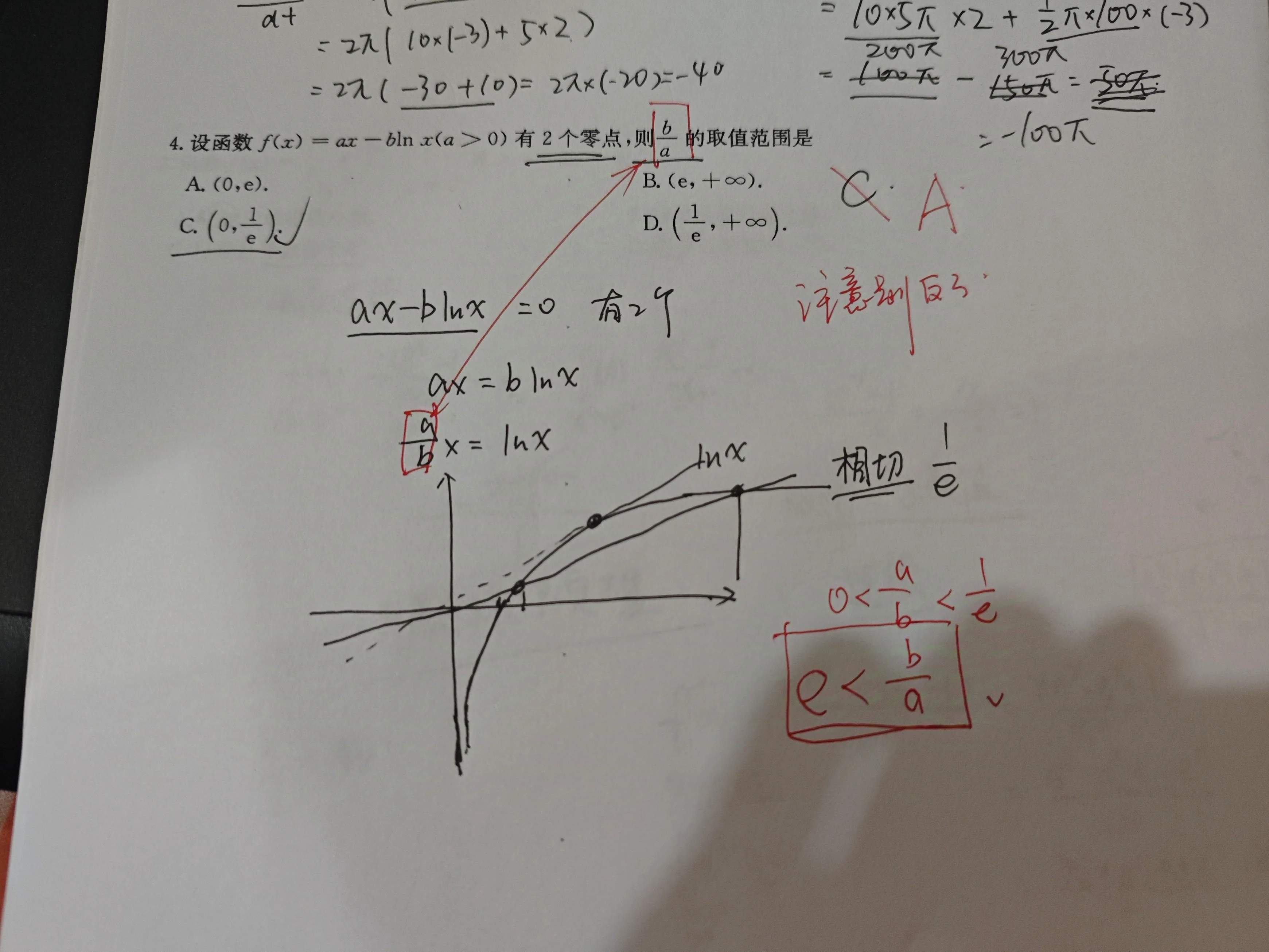
解
[!done]-
可以由
(解) (法一)
下面分析
当
又因为
因此,应选 A.
(法二) 同法一可知
计算
由于
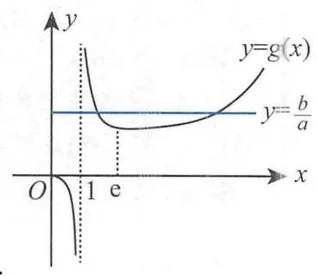
由图可知,曲线
注 ① 实际上,
因此,
② 法二中,也可以令
Jun 19, 20255 min read
[!question]+
设函数
(A)
(B)
(C)
(D)
[!NOTE]+
这里也是粗心的问题导致算错了,问的是b/a,我算的是a/b

[!done]-
可以由
(解) (法一)
下面分析
当
又因为
因此,应选 A.
(法二) 同法一可知
计算
由于

由图可知,曲线
注 ① 实际上,
因此,
② 法二中,也可以令