题10
题目
[!error]+
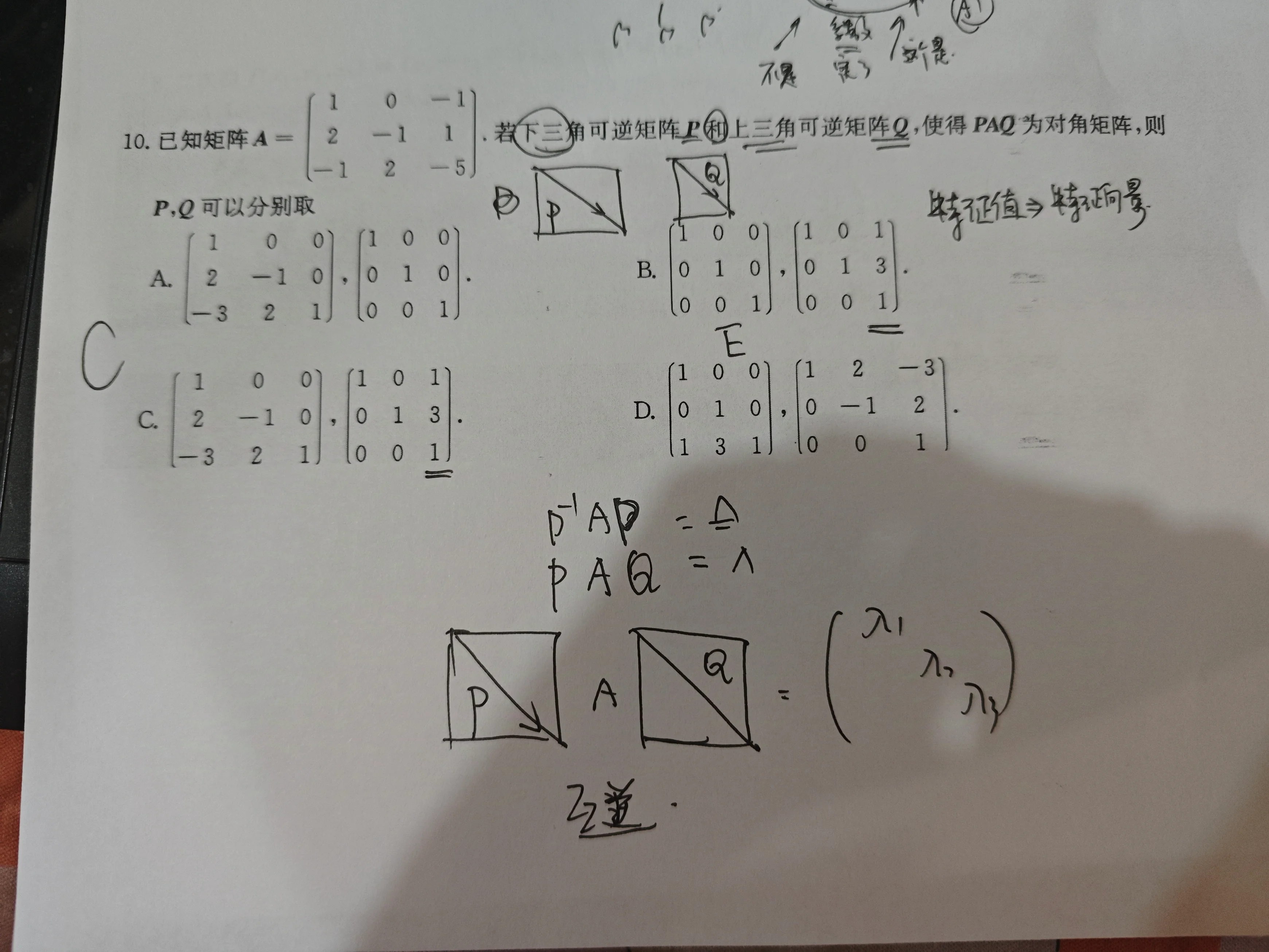
Q:已知矩阵 ,若存在下三角可逆矩阵 与上三角可逆矩阵 ,使 为对角矩阵,则 可分别为 ( )
(A) .
(B) .
(C) .
(D) .
分析
[!NOTE]+
A:注意可逆矩阵这个条件,说明可以通过做出的初等变换得到
解
[!done]-
对矩阵左乘一个初等矩阵相当于对矩阵作一次初等行变换, 左乘一个可逆矩阵相当于对矩阵作一系列初等行变换; 对矩阵右乘一个初等矩阵相当于对矩阵作一次初等列变换, 右乘一个可逆矩阵相当于对矩阵作一系列初等列变换.
当已知矩阵 通过初等变换化为对角矩阵 ,即存在可逆矩阵 ,使得 时,我们可以通过如下操作找到记录初等行变换的可逆矩阵 与记录初等列变换的可逆矩阵 .
① 对 作初等行变换. 当 变成上三角矩阵 时, 变成 ,即 .
② 对 作初等列变换. 当 变成对角矩阵 时, 变成 ,即 .
解 (法一) 对 作初等行变换.
( 表示对第 行作初等行变换后所得新的第 行,每作一次初等行变换,加一个 .)
取 .
记 ,对 作初等列变换.
取 .
此时, 为对角矩阵. 因此,应选 C.
(法二) 代入法.
观察选项 、 发现,其中各有一个单位矩阵.
由于左乘矩阵相当于对原矩阵作行变换, 右乘矩阵相当于对原矩阵作列变换, 故
的第一列为 的第一列,即 ,
的第一行为 的第一行,即 ,而任何矩阵与单位矩阵相乘所得结果均为原矩阵,于是选项 、 所给 均不能使得 为对角矩阵. 由此可排除选项 、 .
将选项 中的两个矩阵代入计算,可得
由此可见选项 正确. 应选 .
简单计算可验证选项 D 不正确.
的第一行、第二行与 的第一行、第二行相同,即 ,
记为 再右乘 ,则新矩阵的第一列为 . 于是,所得结果不是对角矩阵.
