题8
题目
[!question]+
设
(A)
(B)
(C)
(D)
分析
[!NOTE]+
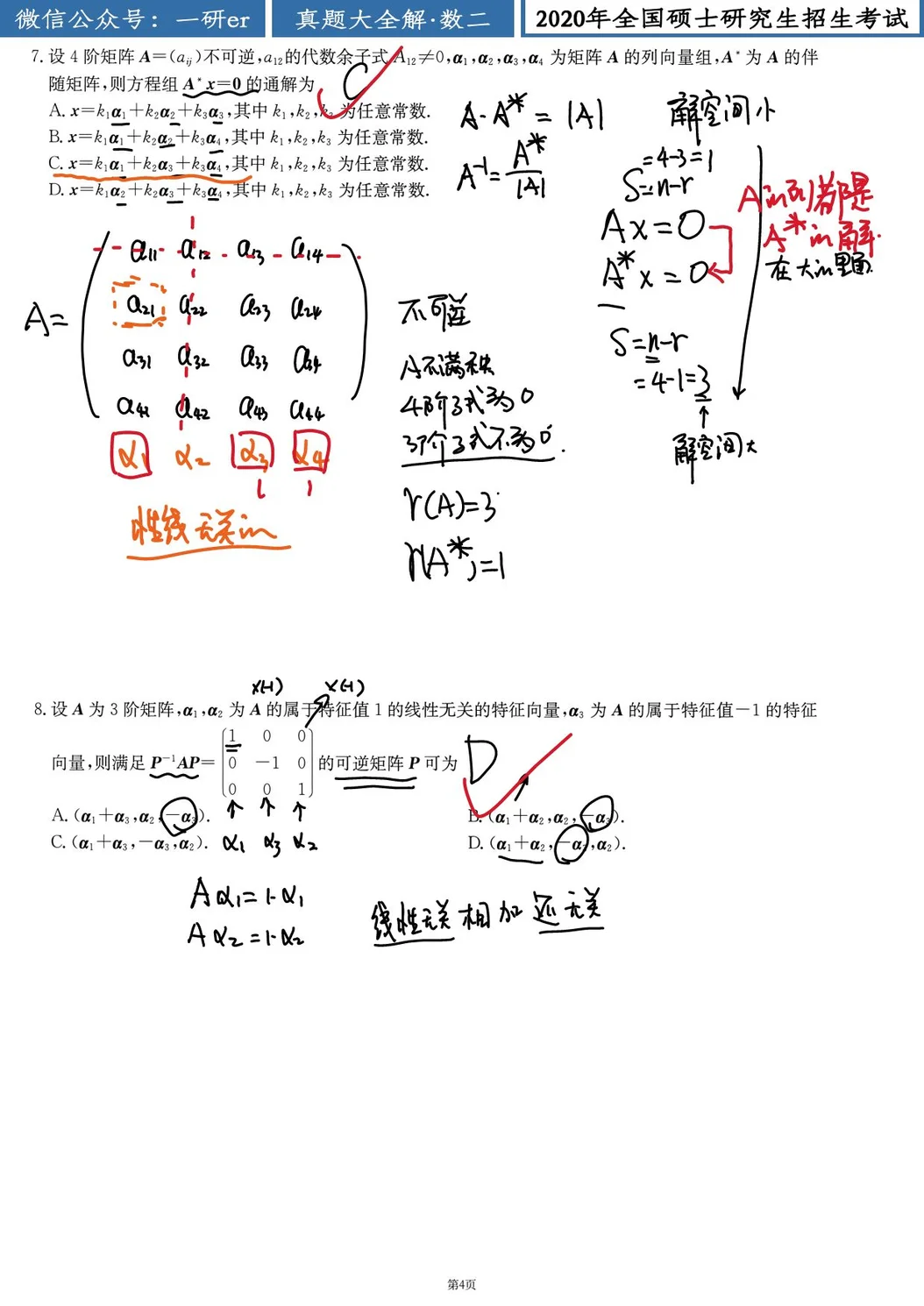
解
[!done]-
所求可逆矩阵
解 由于
第 1 列与第 3 列为属于特征值 1 的线性无关的特征向量.
由已知条件,
由于
因此,
Jun 19, 20252 min read
[!question]+
设
(A)
(B)
(C)
(D)
[!NOTE]+

[!done]-
所求可逆矩阵
解 由于
第 1 列与第 3 列为属于特征值 1 的线性无关的特征向量.
由已知条件,
由于
因此,