题21
题目
[!question]+
设函数
分析
[!NOTE]+

解
[!done]-
解 点
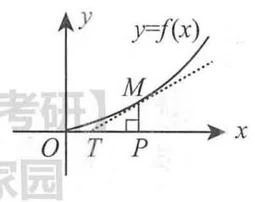
计算
曲线
令
由于
由定积分的几何意义可得,曲边三角形
由曲边三角形
对 (1) 式两端同时求导可得,
整理可得
这是一个可降阶微分方程. 令
由
分离变量可得
综上所述,
[!question]+
设函数
[!NOTE]+

[!done]-
解 点

计算
曲线
令
由于
由定积分的几何意义可得,曲边三角形
由曲边三角形
对 (1) 式两端同时求导可得,
整理可得
这是一个可降阶微分方程. 令
由
分离变量可得
综上所述,