题6
题目
[!question]+
已知 阶可导且 2 阶导函数在 处连续,则 是曲线 和 在 对应的点处相切且曲率相等的 ( )
(A) 充分非必要条件.
(B) 充分必要条件.
(C) 必要非充分条件.
(D) 既非充分又非必要条件.
分析
[!NOTE]+
我们再默写一遍曲率的公式:,原函数和高阶导数之间等式关系,我们通过泰勒公式来得到,注意这个条件,典型的极限的运算法则里面,分式的极限之比,得到其中一个是0倒推出另一个是0的运用

解
[!done]-
两条曲线相切, 能推出两曲线在切点处的切线斜率相等, 即对应的函数在切点横坐标处导数相等. 切点处曲率相等说明两条曲线在该点处的弯曲程度相等,从而由曲率的计算公式 可知切点处对应的二阶导数绝对值相等,但是并不能说明二阶导数相等. 在分析充分性与必要性的时候, 要注意这一点.
解 由 在 处的二阶泰勒公式可得,
代入 可得,
由上式可知 当且仅当
曲线 与 在 对应的点处相切当且仅当 又由曲率的计算公式 以及 可得两条曲线在 对应的点处曲率相等.
因此, 是曲线 和 在 对应的点处相切且曲率相等的充分条件.
注意到两曲线在 对应的点处曲率相等只能说明 ,但并不能推出 ,故 不是曲线 和 在 对应的点处相切且曲率相等的必要条件.
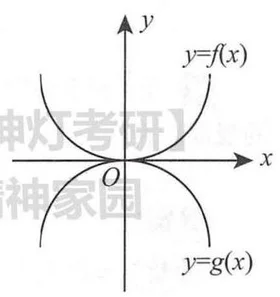
例如: 取 这两条曲线均为半径为 1 的半圆弧 (圆弧上各点的曲率半径均为 1 ). 于是, 各点处曲率相等, 均等于 1 . 如图所示, 这两条曲线在原点处相切, 但 在 上是凹曲线, 在 上是凸曲线,
综上所述, 应选 A.

