题18
题目
[!question]+
已知平面区域
分析
[!NOTE]+
二重积分画不出来图怎么办?不慌!尝试用极坐标算二重积分来画这个图,或者奇偶性化简二重积分,我们看看积分区域的奇偶性来确定图形的大致性质,看看能不能化简,这种类似的区域我们也画过:题18

解
[!done]-
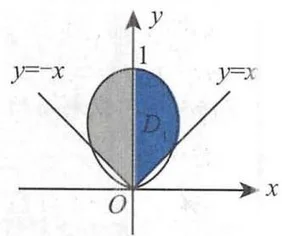
通过观察可知,本题中的区域
解 如图所示,区域
由于
在极坐标系下计算
写出区域
边界曲线
因此,
Jun 19, 20253 min read
[!question]+
已知平面区域
[!NOTE]+
二重积分画不出来图怎么办?不慌!尝试用极坐标算二重积分来画这个图,或者奇偶性化简二重积分,我们看看积分区域的奇偶性来确定图形的大致性质,看看能不能化简,这种类似的区域我们也画过:题18

[!done]-

通过观察可知,本题中的区域
解 如图所示,区域
由于
在极坐标系下计算
写出区域
边界曲线
因此,