题16

题16

题目

[!question]+
求不定积分 .

分析

[!NOTE]+
部分分式积分法一定要记住，这里的分母已经是分式乘积了，我们直接拆分进行拆项就可以了

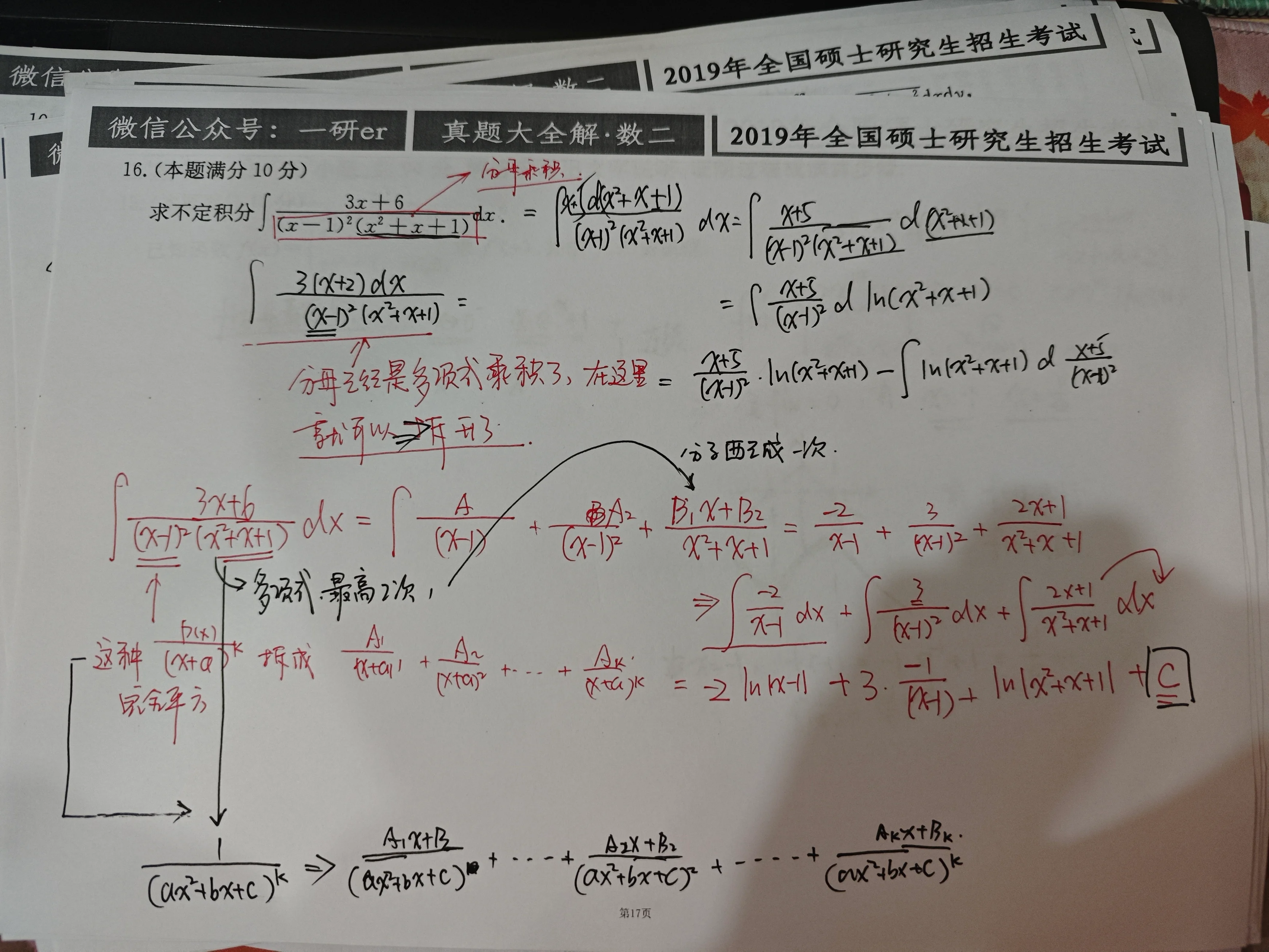
解

[!done]-
本题中的被积函数是有理分式, 故计算它的不定积分时, 需先对其进行部分分式分解. 根据分母的特点, 可作如下分解:

利用待定系数法求得 再积分.

解 设

通分并整理可得,

比较 的系数以及常数项可得,

由 (1) 式可得 . 代入 (4) 式可得

(5) 式与(3) 式相减,可得 ,即 . 分别代入(2) 式与(3) 式,可解得 . 从而 .

因此,

其中 为任意常数.

注 “ ” 处的积分结果 可以不写绝对值符号是因为 恒大于零.

有理函数积分的一般步骤

将有理函数写成多项式加真分式的形式, 并对真分式进行部分分式分解, 再分别积分.

真分式的部分分式分解的一般方法

对真分式 ,

(1) 若 含有因式 ,则分解后所得表达式包含

其中 均为常数.

(2) 若 含有因式 ,其中 ,即二次三项式 无实根, 则分解后所得表达式包含

其中 均为常数.

以有理分式 为例.

注意到 有实根,故原有理分式应写为 后再按照上述方法分解. 分解后所得表达式应为

按照此种方法分解得到的表达式是唯一的.