题16

题16

题目

[!question]+
已知连续函数 满足 .
(I) 求 ;
(II) 若 在区间 上的平均值为 1,求 的值.

分析

[!NOTE]+
虽然以前考过变上限积分，拿去在积分，然后我们用来分部积分凑微分把这个变限积分求导公式的考法。但是呢，这个题，考的其实直接是对这个变限积分求导然后我们得到一个微分方程。总之就是看见变限积分一定要想是不是要求导，能先求导就先求导，不能先求导，我们再考虑说拿去在积分或者说凑分部积分。

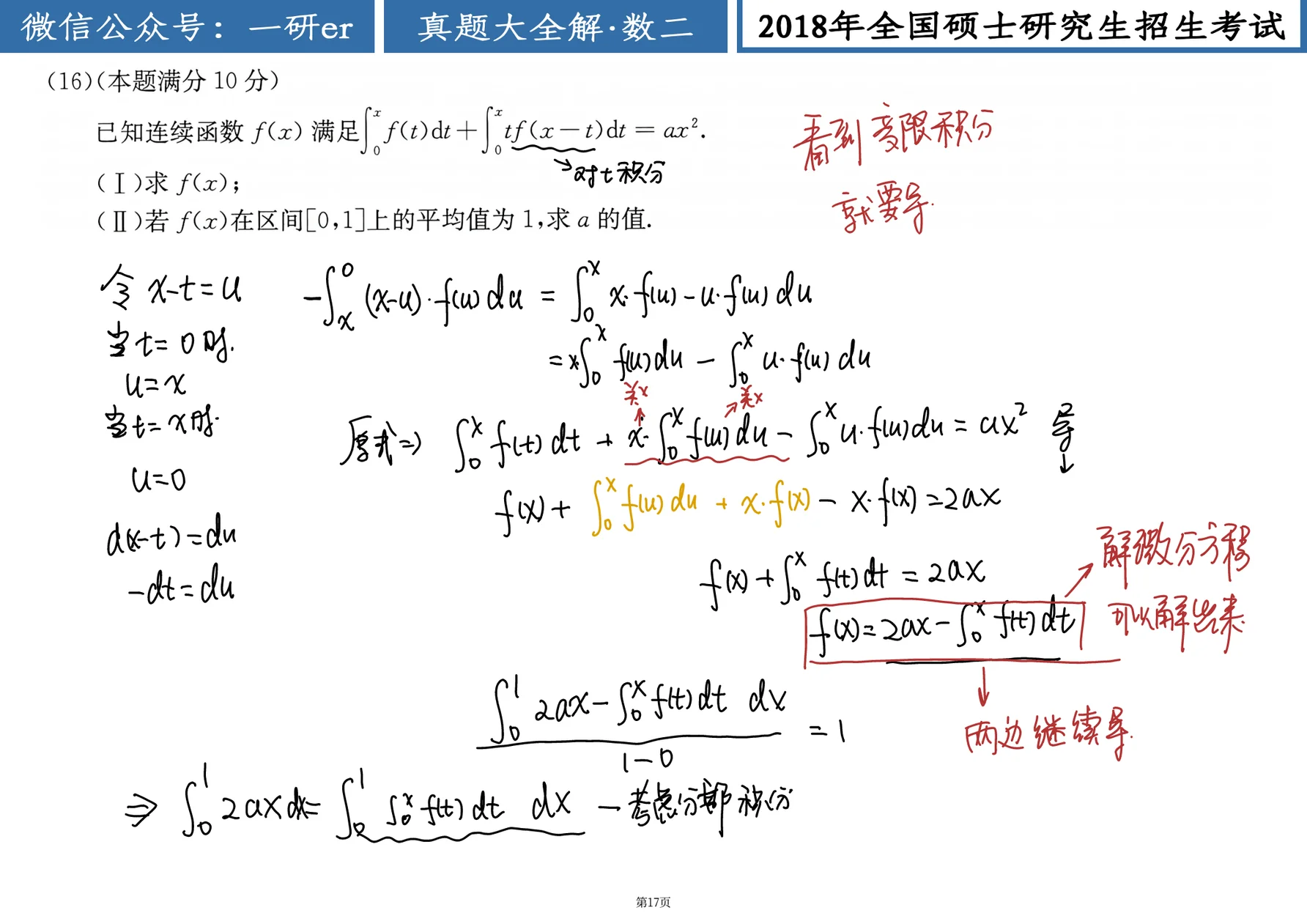
解

[!done]-
第 (I) 问中，对已知等式关于 求导，可得关于 的一阶微分方程，解该微分方程，并代入初始条件，可以得到 的表达式。在求导时，需要注意 的被积函数中含有参变量 ，应先利用换元法将其转化为被积函数不含参变量 的变限积分再求导。此外，需注意利用已知等式得到初始条件。

第 (II) 问中，要用到函数在区间上的平均值的定义。该概念在 2016 年第 (21) 题中也考查过，希望引起大家的注意。

函数 在区间 上的平均值为 。

解 (I) 令 ，则

于是，

对 两端关于 求导，可得

，

即

(1)。

由 (1) 式可知，，而 连续，故 可导，从而 可导。

对 (1) 式两端关于 求导，可得

。

这是一个一阶非齐次线性微分方程。由求解公式可得，

其中 为待定常数。

在 (1) 式中，令 ，可得 。将 代入 可得，，即 。

因此，。

(II) 根据平均值的定义，，即 。

由于

故 。解得 。

因此，。