题3
题目
[!question]+
(3) 设数列
(A) 当
(B) 当
(C) 当
(D) 当
分析
[!NOTE]+
又是这种数列极限和函数之间是否一一对应,然后判断收敛与否的问题
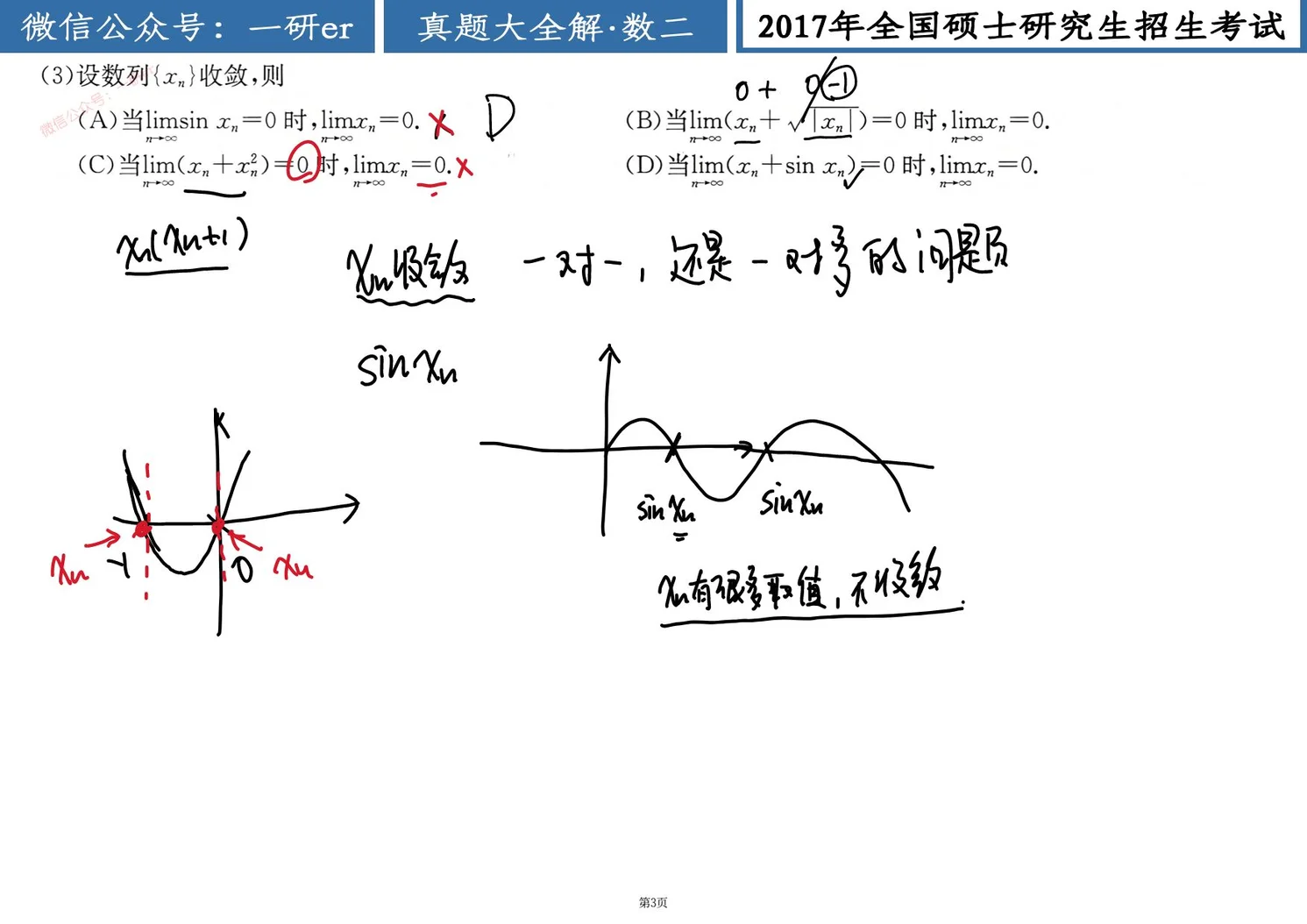
解
[!done]-
若数列
对本题而言, 排除法是较快的解法.
解 (法一) 记
注意到
(法二) 记
由于
应选 D.
(法三) 排除法.
对选项 A: 考虑
对选项 B 和选项 C: 考虑
但
由排除法知,应选 D.
注 本题可以从如下角度来考虑反例的选取.
注意到四个选项中出现的函数均为连续函数,而对连续函数
选项
选项
选项
选项 D:
因此,选项