题23
题目
[!question]+
设二次型
分析
[!NOTE]+
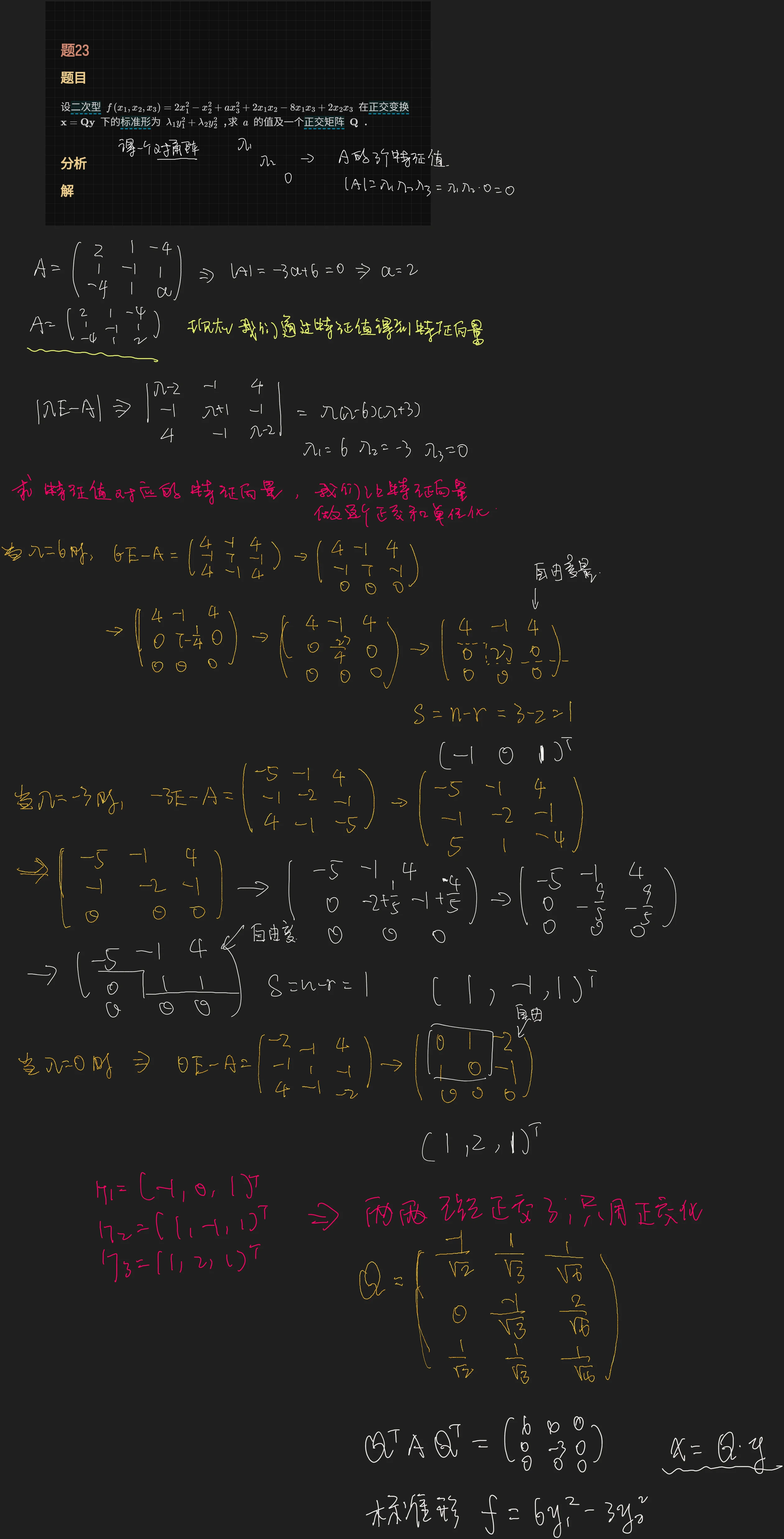
解
[!done]-
解 记二次型
由于
计算
因此,
计算
于是,
当
当
当
由于实对称矩阵对应于不同特征值的特征向量相互正交,故只需要将所得特征向量单位化。
将
注 得到
Jun 19, 20255 min read
[!question]+
设二次型
[!NOTE]+
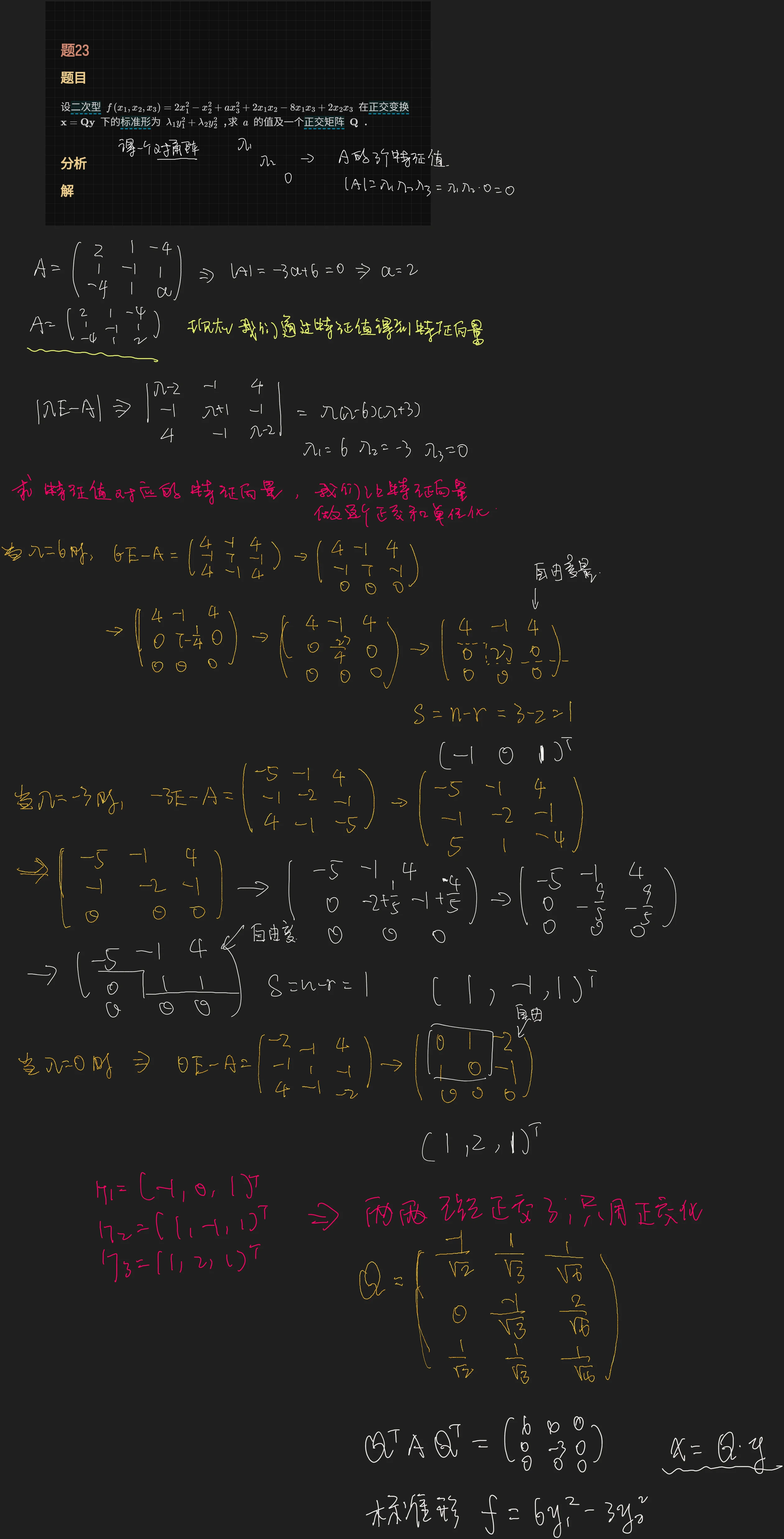
[!done]-
解 记二次型
由于
计算
因此,
计算
于是,
当
当
当
由于实对称矩阵对应于不同特征值的特征向量相互正交,故只需要将所得特征向量单位化。
将
注 得到