题2
题目
[!question]+
(2) 设二阶可导函数 满足 且 ,则 ( )
(A) .
(B) .
(C) .
(D) .
分析
[!NOTE]+
画图是对的,但是不能纯拿眼睛看,还是得把它设出来,小题大做,这个属于是该拿到的分
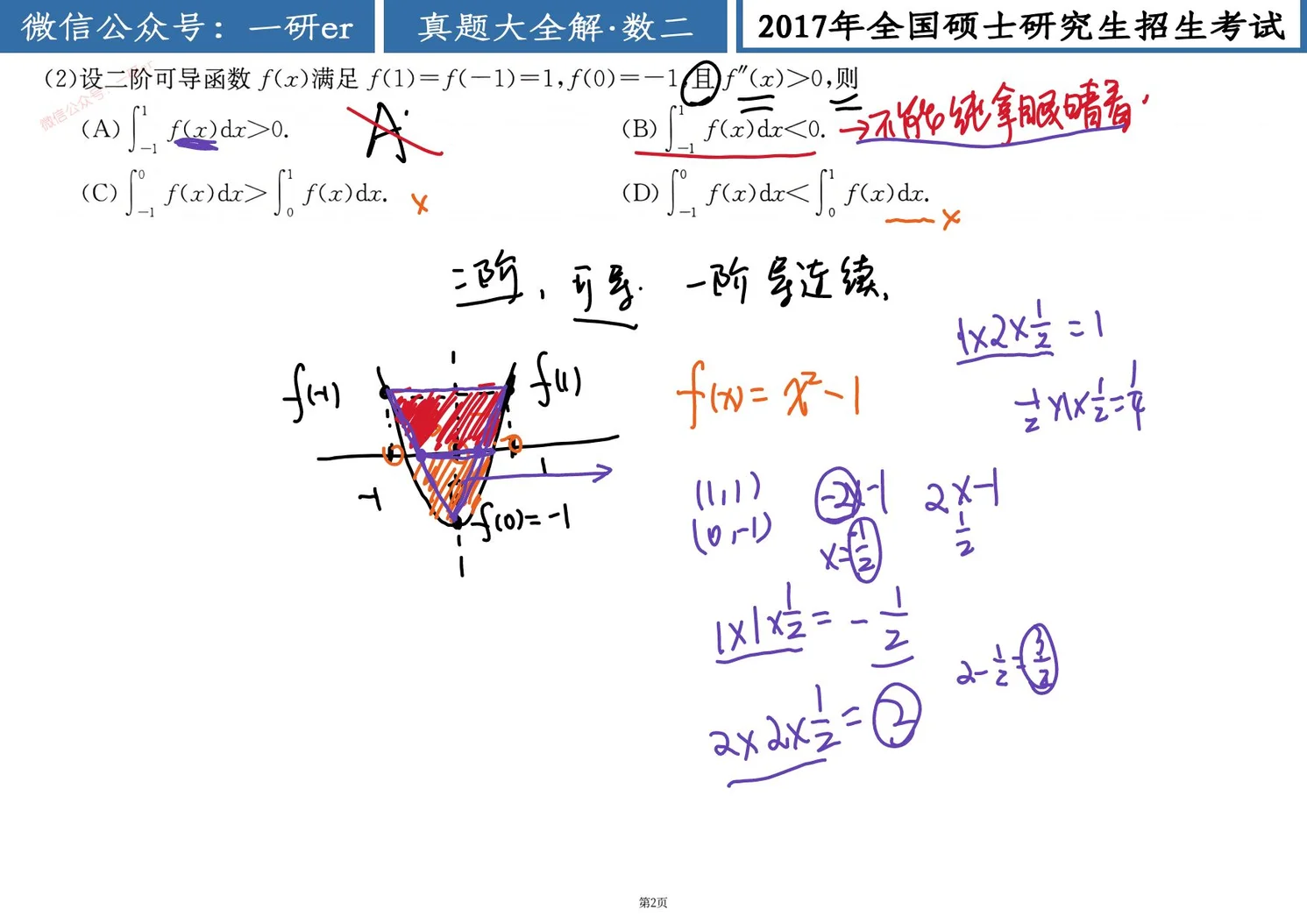
解
[!done]-
(解) (法一) 如图所示,用直线连接点 . 记这三点所过折线为 . 根据 ,求得 关于 轴对称.
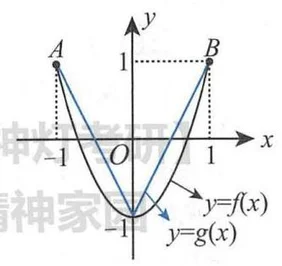
由于 ,故 是凹曲线. 根据凹曲线的性质,曲线 位于曲线 以下,即 ,等号仅在 处取得. 因此,
应选 B.
(法二) 记 ,则 在 上可导.
对 上的 使用拉格朗日中值定理,可得 ,其中 . 由 可知, . 代入 (1) 式,可得
于是, 在 上单调增加, ,即 .
因此,
同理讨论 上的 可得 在 上单调增加,从而 . 于是对 上的 ,有 . 因此,
综上所述, . 应选 B.
(法三) 排除法.
取特殊的 ,使其满足 ,且 .
由于 ,故不妨取二次函数 ,且 . 代入点 和 ,可解得 . 于是,设 . 由于
对称性
故可排除选项 A.
进一步,可验证对 ,
可排除选项 和选项 . 因此,应选 .
注 法一通过凹曲线的几何性质得到 .
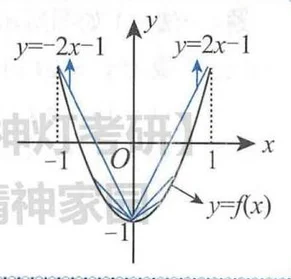
法二反映了凹曲线的另一个几何性质,实际上是将 证明了一遍. 如图所示, 实际上为连接曲线 上两点 的弦的斜率. 对凹曲线来说, 是单调增加函数,故对 ,整理即得 .


