题5
题目
[!question]+
设函数
(A)
(B)
(C)
(D)
分析
[!NOTE]+
解
[!done]-
(解) (法一) 首先,由于函数
另一方面,由于
由
考虑函数
综上所述,应选 A
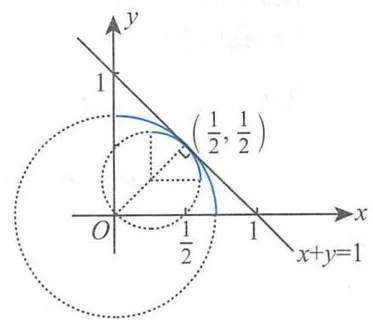
(法二) 特殊值法。我们将题中的两条曲线分别取作两段圆弧。
以点
这两段圆弧均为凸曲线,且在点
Jun 19, 20253 min read
[!question]+
设函数
(A)
(B)
(C)
(D)
[!NOTE]+

[!done]-
(解) (法一) 首先,由于函数
另一方面,由于
由
考虑函数
综上所述,应选 A

(法二) 特殊值法。我们将题中的两条曲线分别取作两段圆弧。
以点
这两段圆弧均为凸曲线,且在点