题20
题目
[!question]+
设
分析
[!NOTE]+
旋转体侧面积和旋转体的体积的问题,这里我们要把这个参数方程解出来然后硬算都是可以的


解
[!done]-
解 区域
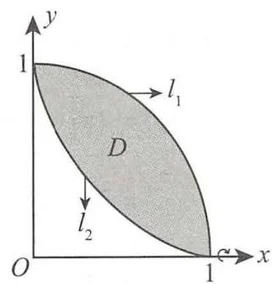
记曲线
此外,可求得两条曲线的交点为
下面我们用两种方法来计算所得旋转体的体积与表面积.
(法一) 利用
因此,
(法二) 写出曲线
由
下面计算
因此,
Jun 19, 20255 min read
[!question]+
设
[!NOTE]+
旋转体侧面积和旋转体的体积的问题,这里我们要把这个参数方程解出来然后硬算都是可以的


[!done]-
解 区域

记曲线
此外,可求得两条曲线的交点为
下面我们用两种方法来计算所得旋转体的体积与表面积.
(法一) 利用
因此,
(法二) 写出曲线
由
下面计算
因此,