题14

题14

题目

[!question]+
设矩阵 与矩阵 等价,则

分析

[!NOTE]+
不要对实对称矩阵矩阵用sherman-morrison公式，这里用了，但是错了，没把这个行列式算对，实对称的，直接用行和相等的方法算就可以了

解

[!done]-
解 (法一) 记 .

( 表示对第 行作初等行变换后所得新的第 行,每作一次初等行变换,加一个 .)

于是 .

由于 等价,故 ,从而 .

另一方面,计算 得,

当且仅当 或 . 当 时, ,不符合题意. 因此, .

(法二) 由法一知, .

对 作初等行变换,

当 ,即 或 时, . 又由于当 时, ,

故舍去.

因此, .

注 两个同型矩阵等价, 当且仅当它们的秩相等, 而两个同型矩阵的秩相等仅仅只是它们矩阵合同或者矩阵相似的必要条件.

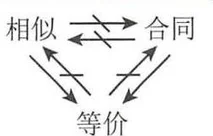
对于一般矩阵来说, 合同不能推出相似, 而相似也不能推出合同.