题4

题4

题目

[!error]+
Q:设函数在 内连续,其 2 阶导函数 的图形如右图所示,则曲线 的拐点个数为 ( )

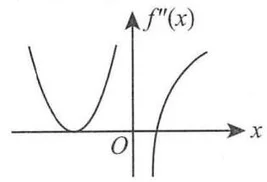
(A) 0 .
(B) 1 .
(C) 2 .
(D) 3 .

分析

[!NOTE]+
A:考察了拐点的判定，我做错了，我的直觉是：判断二阶导的变号零点来判定拐点，只能说我的直觉对了一部分，首先：二阶导为0不是判断拐点的充要条件这个确实，其次，我们如果要看0点，这个零点必须是变号0点，也就是我的直觉。但是，如果在某点无定义，同时在该点左右两侧是变号的，这个点同样可以拐点，这也就是驳斥了二阶导为0是拐点，和我的默认直觉，只看了变号零点的问题

解

[!done]-
曲线可能的拐点需考虑二阶导数不存在的点和二阶导数为零的点. 若 在 的某去心邻域内二阶可导, 满足 或者 不存在，且 在 左、右两侧异号,则点 为拐点.
解 由图可知,在 上, 有两个实根 ,且 在 处无定义.
下面我们分别讨论点 和 是否为拐点.

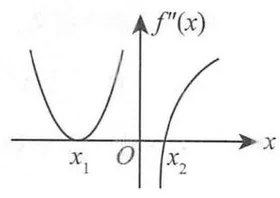
在 的左、右邻域内, 均大于零. 在该点两侧不变号, 故点 不是曲线 的拐点.
在 的左侧邻域内, ; 在 的右侧邻域内, . 在该点两侧变号,故点 是曲线 的拐点.
在 的左侧邻域内, ; 在 的右侧邻域内, 在该点两侧变号,故点 是曲线 的拐点.
综上所述,曲线 共有 2 个拐点,应选 C.
注 ① 注意: 不是拐点的充分条件. 本题中的点 满足 ,但却不是曲线 的拐点. 此外,不要漏掉 不存在的点. 本题中, 在 处不存在,但点 是曲线 的拐点.
② 本题也可以利用下述判别法来判定点 为拐点. 若函数 在点 处三阶可导且 ,则点 为曲线 的拐点.
从图中可以看出曲线 在点 处切线的斜率大于零,从而 . 因此由上述判别法可得点 为拐点,但不能确定其他两点是否为拐点.