题21
题目
[!question]+
已知函数
分析
[!NOTE]+

解
[!done]-
(证) 首先,由于过点
因为
因此,
如图 (a) 所示,记点
下面我们用两种方法证明
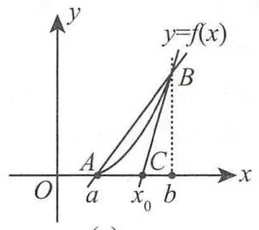
(a)
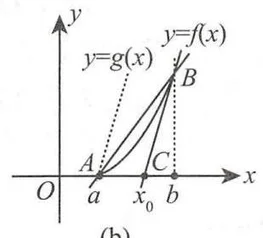
(法一) 由拉格朗日中值定理可得,存在
代入
(法二) 要证
该不等式的几何意义为过点
记
由拉格朗日中值定理,有
由于对任意的
因此,
综上所述,
Jun 19, 20254 min read
[!question]+
已知函数
[!NOTE]+

[!done]-
(证) 首先,由于过点
因为
因此,
如图 (a) 所示,记点
下面我们用两种方法证明

(a)

(法一) 由拉格朗日中值定理可得,存在
代入
(法二) 要证
该不等式的几何意义为过点
记
由拉格朗日中值定理,有
由于对任意的
因此,
综上所述,