题2

题2

题目

函数 在 内
(A) 连续.
(B) 有可去间断点.
(C) 有跳跃间断点.
(D) 有无穷间断点.

分析

这个题目我们做过：题1.4，这里我是考虑先以t为极限的变量，把这个fx解出来，然后看的是以x为变量的函数是否连续，我们把目光放在t上，这是一个无穷小的无穷大次，可以直接解出来。这里我对可去间断点还是存在理解错误，一直没搞清楚，可去间断点是指，函数在这个点上的极限存在，但是函数值和极限不相等（或者说该点无定义）这个题目就是0这里做了分母，没有定义，但是两侧极限是相同的，所以是可去的

解

解 由 的表达式可以看出, 在 处无定义.
当 时, .
下面我们用两种方法计算 .
(法一) 凑重要极限.

(法二) 取对数.

于是,当 时, . 因此, 为 的可去间断点. 应选 B.
注 本题可能让人困惑的地方是 的形式. 是以 型未定式极限的形式出现的. 对 的正确理解: 固定一个 (例如 ),考虑以 为变量的极限过程,所得极限值即 所对应的 (例如 ). 由于分母不能为零,故 为 的间断点,可通过求 来判断 的间断点类型.
间断点的定义 设函数 在点 的去心邻域内有定义. 若 满足下列情形之一,
在 没有定义;
在 有定义, 不存在或者 存在但 ,则称 在 不连续, 为 的间断点.

间断点的分类

类型	定义	相关概念
第一类间断点	与 均存在	可去间断点、跳跃间断点
第二类间断点	至少有一个不存在	无穷间断点、振荡间断点

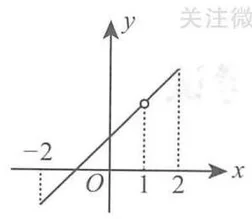
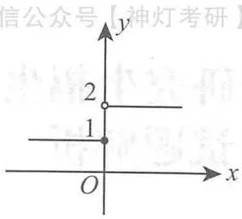
• 可去间断点满足 . 例如: 为 的可去间断点,如图 (a).
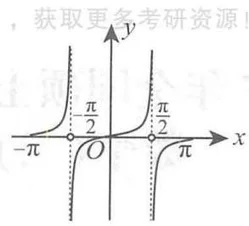
• 跳跃间断点满足 . 例如: 为 的跳跃间断点,如图 (b).
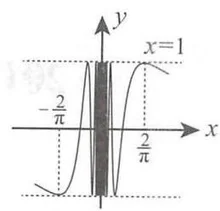
• 无穷间断点满足 至少有一个为 . 例如: 为 的无穷间断点,如图 (c). 注意: 在 的左、右极限不相等. .
• 振荡间断点满足在该间断点附近,函数值在某个区间内变动无限多次. 例如: . 为 的振荡间断点,如图(d).

解本题首先应当找出函数的间断点, 再通过求函数在间断点处的极限来判断其类型.