题8
题目
[!question]+
设 均为 3 维向量,则对任意常数 ,向量组 线性无关是向量组 , 线性无关的 ( )
(A) 必要非充分条件.
(B) 充分非必要条件.
(C) 充分必要条件.
(D) 既非充分也非必要条件.
分析
[!NOTE]+
注意我们判断向量组是否线性无关的时候,常常自己设置系数,而忘记了我们还可以自己设置向量,只要找到了一个反例的向量组,也就证明了成立和不成立,我这里有点纠结也是这个原因,因为我在这个系数上面纠结上了
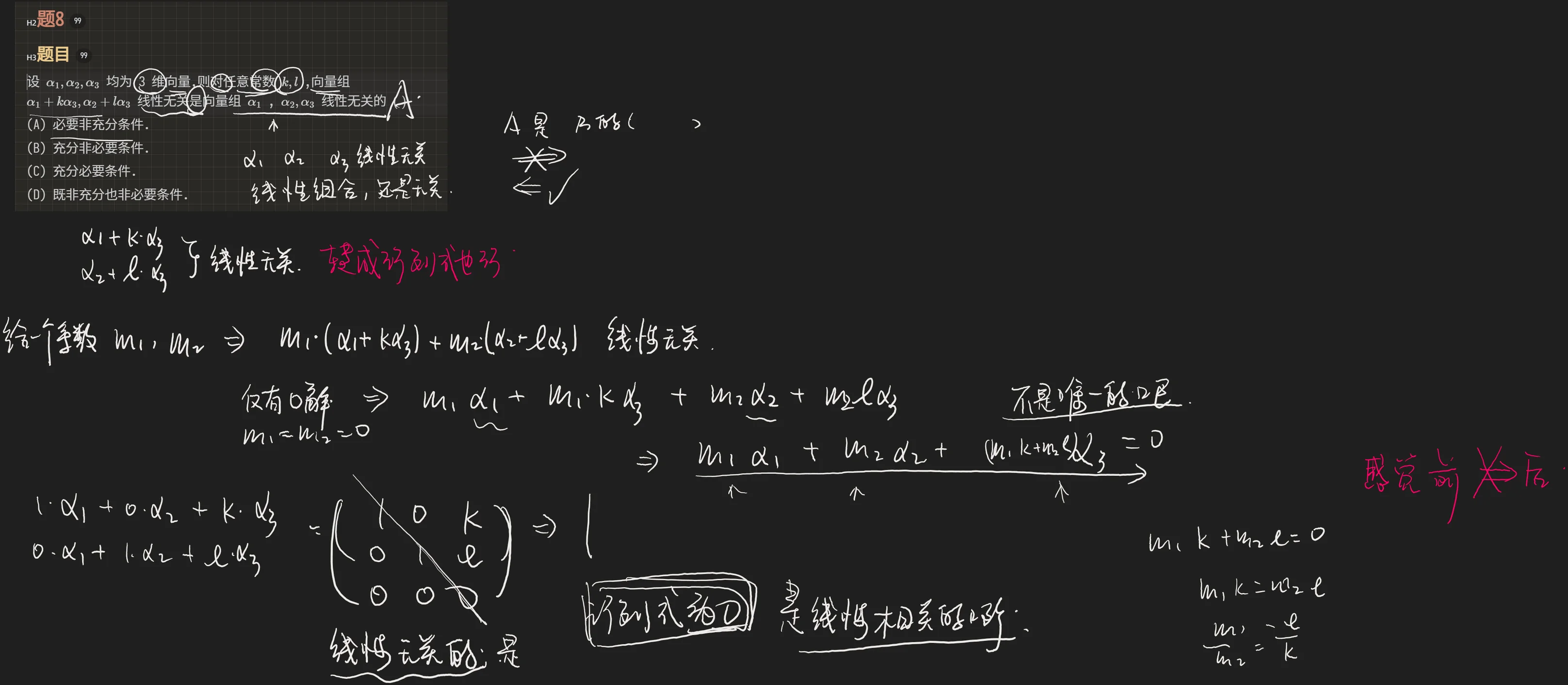
解
[!done]-
向量组线性无关的定义 给定向量组 ,若由
能得到 均为零,则称向量组 是线性无关的,否则称它线性相关,即存在不全为零的数 使得 (1) 式成立.
解 假设 线性无关. 考虑向量组 .
由于 ,故由 线性无关可知, . 因此, 线性无关. 向量组 线性无关是向量组 线性无关的必要条件.
但是向量组 线性无关不是向量组 线性无关的充分条件.
下面我们给出反例. 令 线性无关,而 ,则此时 线性无关. 对任意非零常数 ,有 ,从而 线性相关.
因此, 线性无关是向量组 线性无关的必要非充分条件. 应选 A.
注 正确解答本题需要一定的逻辑推理能力. 请大家注意充分条件与必要条件的区别与联系.
充分条件与必要条件 若命题 能推出命题 ,则称命题 是命题 的充分条件,或命题 是命题 的必要条件.