题3
题目
[!question]+
设函数
(A) 当
(B) 当
(C) 当
(D) 当
分析
[!NOTE]+

解
[!done]-
分析 本题主要考查曲线的凹凸性. 对此类题, 常用数形结合的方法.
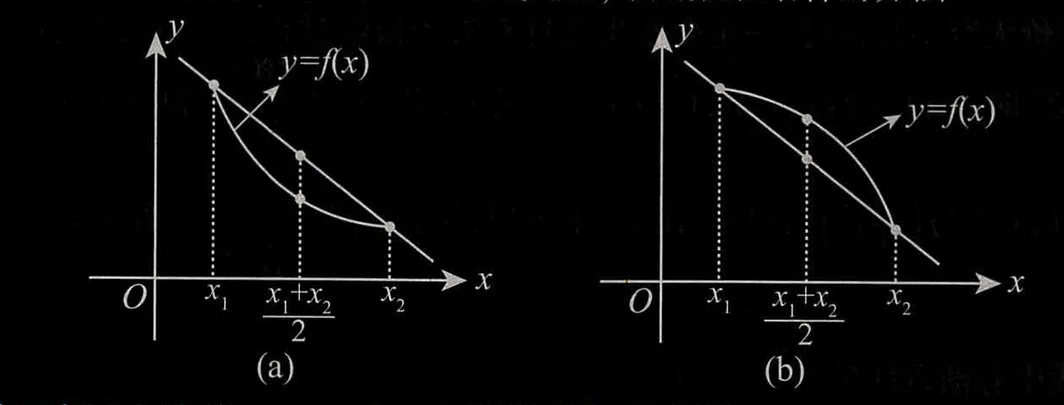
设
- 若恒有
,则称曲线 在区间 上凹,如图 (a); - 若恒有
,则称曲线 在区间 上凸,如图(b).
从图形上看,过凹曲线
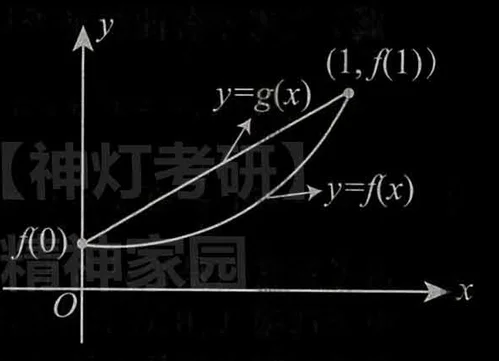
解 由于
由分析知,若
一阶导数的符号与曲线的凹凸性没有直接关系. 作为选项
Jun 19, 20253 min read
[!question]+
设函数
(A) 当
(B) 当
(C) 当
(D) 当
[!NOTE]+

[!done]-
分析 本题主要考查曲线的凹凸性. 对此类题, 常用数形结合的方法.

设
从图形上看,过凹曲线

解 由于
由分析知,若
一阶导数的符号与曲线的凹凸性没有直接关系. 作为选项