题21
题目
[!question]+
已知函数
曲线
分析
[!NOTE]+
这是不规则的,不是坐标轴的旋转体的体积,不能直接套公式,这里要理解公式再操作,这里是隐函数,一时之间找不到函数
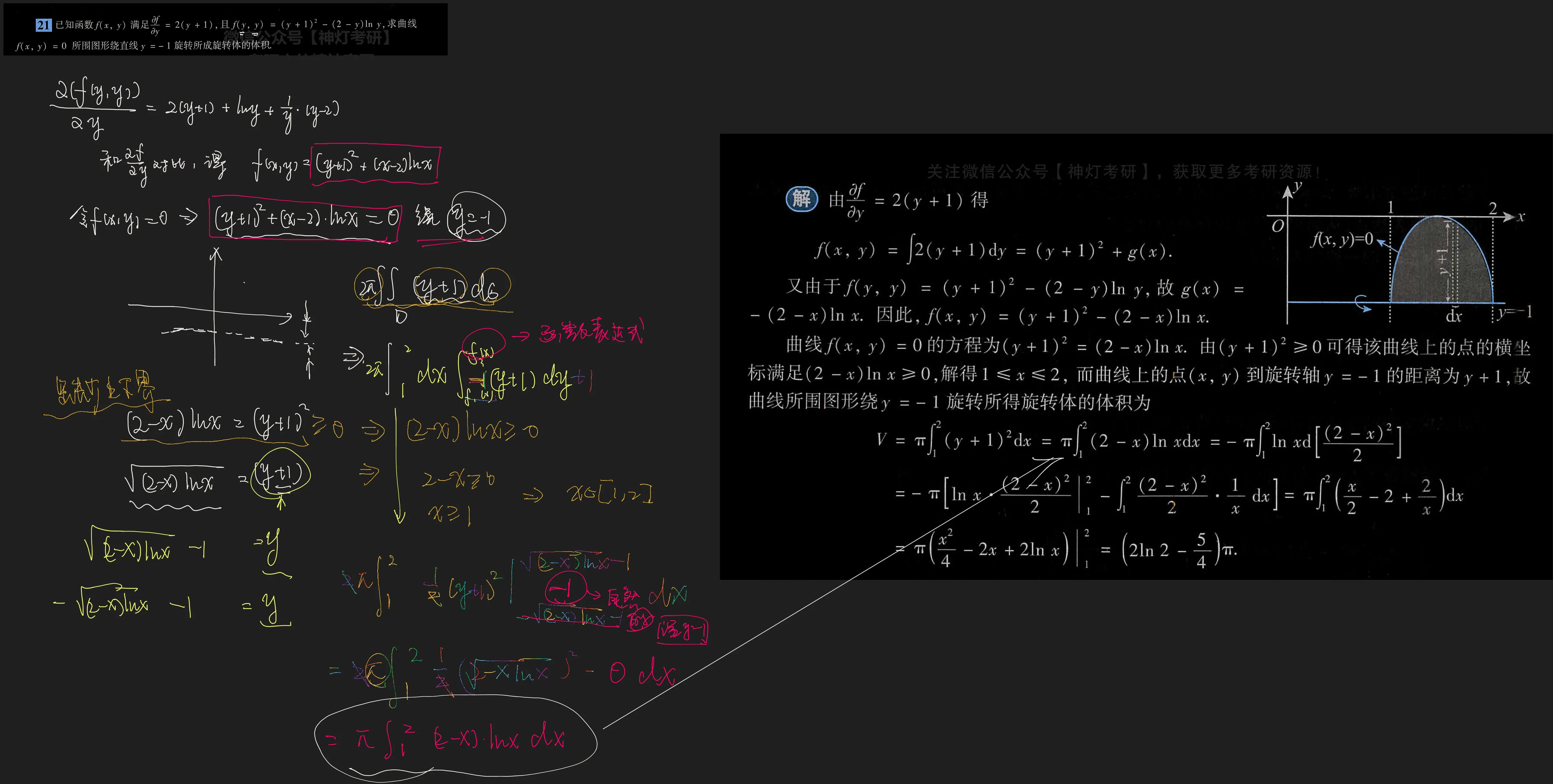
解
[!done]-
解 由
又由于
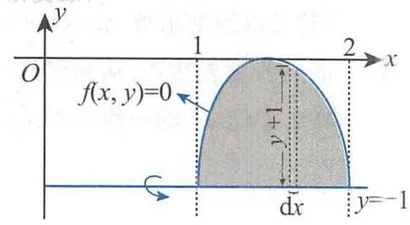
曲线
注 求本题中旋转体的体积, 并无现成的公式可套用. 因此, 我们应该从基本方法出发来求解.
在推导公式
曲线
Jun 19, 20253 min read
[!question]+
已知函数
曲线
[!NOTE]+
这是不规则的,不是坐标轴的旋转体的体积,不能直接套公式,这里要理解公式再操作,这里是隐函数,一时之间找不到函数

[!done]-
解 由

又由于
曲线
注 求本题中旋转体的体积, 并无现成的公式可套用. 因此, 我们应该从基本方法出发来求解.
在推导公式
曲线