题19
题目
[!question]+
设函数
证明:
(I)
(II)
分析
[!NOTE]+
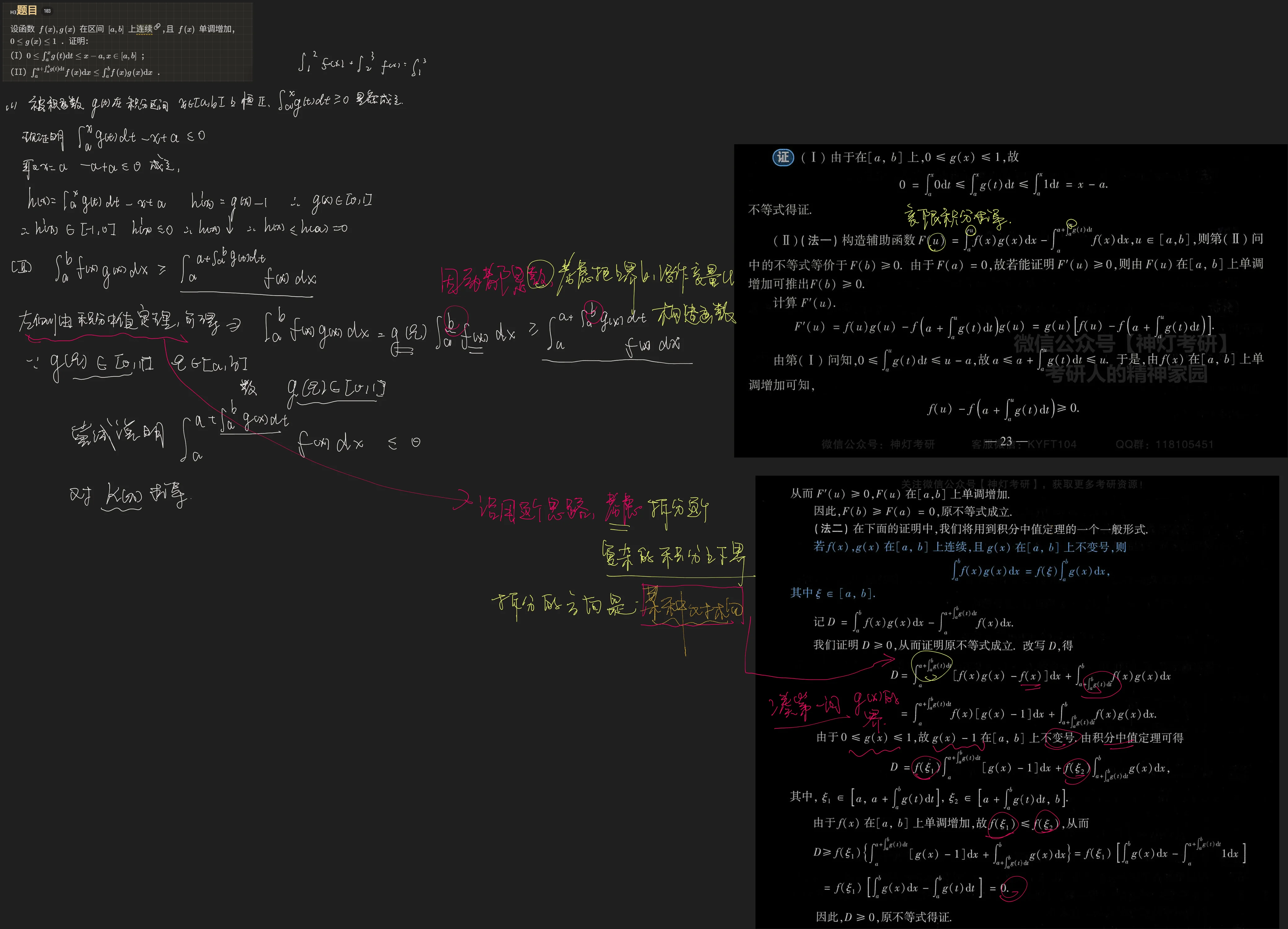
解
[!done]-
(证) (I) 由于在
不等式得证.
(II) (法一) 构造辅助函数
计算
由第
从而
因此,
(法二) 在下面的证明中, 我们将用到积分中值定理的一个一般形式.
若
其中
记
我们证明
由于
其中,
由于
因此,
Jun 19, 20254 min read
[!question]+
设函数
证明:
(I)
(II)
[!NOTE]+

[!done]-
(证) (I) 由于在
不等式得证.
(II) (法一) 构造辅助函数
计算
由第
从而
因此,
(法二) 在下面的证明中, 我们将用到积分中值定理的一个一般形式.
若
其中
记
我们证明
由于
其中,
由于
因此,