题17

题17

题目

[!question]+
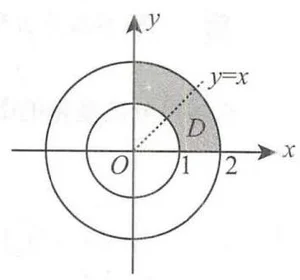
设平面区域 . 计算 .

分析

[!NOTE]+
算二重积分的时候，先看轮换对称性简化二重积分化简和奇偶性化简二重积分，然后再看极坐标算二重积分，算的时候，特别要注意使用华里士公式，和区间再现公式来对三角进行化简，这里每一步，我都没有多想，都在硬算，导致算错了

解

[!done]-
解 记 . 积分区域如图所示.

(法一) 首先,由于积分区域 关于 对称,故对 具有轮换对称性, 从而

因此,

在极坐标系下, .

其中,

因此, .

(法二) 在不使用轮换对称性对 进行化简的情况下计算 .

在极坐标系下, .

由于

故

因此, .

(注) 在法二中,我们用到了 .

事实上,我们有更一般的结论.

设 是定义在 上的连续函数. 利用换元法,我们能证明

令 ,则