题22
题目
[!question]+
设
分析
[!NOTE]+
考虑直接解矩阵方程,我这里因为太复杂了,有一步抄错了,所以没写出来
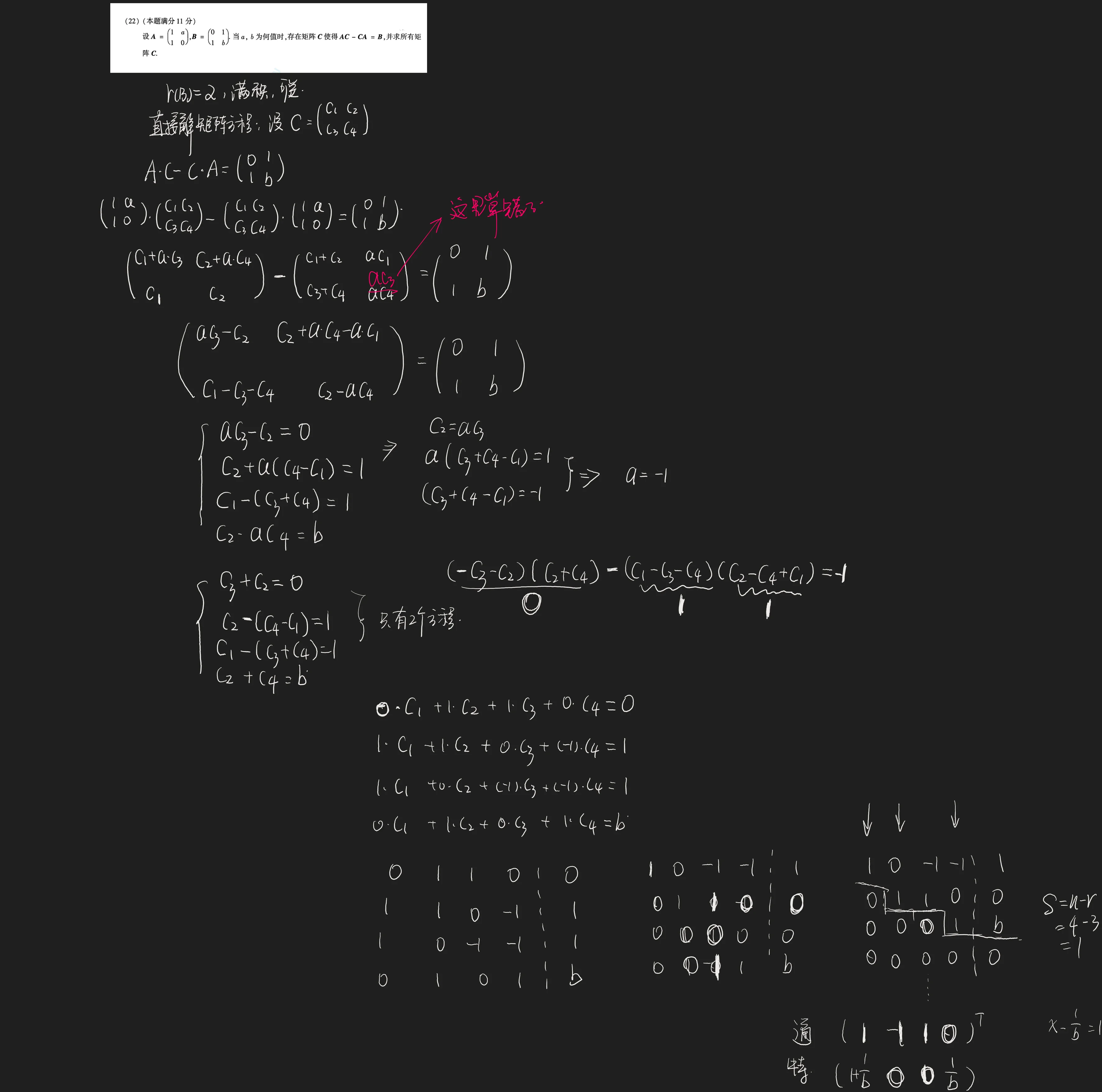
解
[!done]-
关于矩阵的迹,有这样一条性质: 若
解 (法一) 设
写成线性方程组的形式:
记该线性方程组为
当
即
其中
因此,当
(法二) 由于
设
将
从而
注 法二与法一实际上差别不大. 法二中,在确定
Jun 19, 20255 min read
[!question]+
设
[!NOTE]+
考虑直接解矩阵方程,我这里因为太复杂了,有一步抄错了,所以没写出来

[!done]-
关于矩阵的迹,有这样一条性质: 若
解 (法一) 设
写成线性方程组的形式:
记该线性方程组为
当
即
其中
因此,当
(法二) 由于
设
将
从而
注 法二与法一实际上差别不大. 法二中,在确定