题21

题21

题目

[!question]+
设函数 在闭区间 上连续,在开区间 内可导,且 , .
证明: 存在 ,使得 .

分析

[!NOTE]+
拉格朗日中值定理的这种待证明结论里面，是“导+变量”形式出现的，考虑它的原函数，把相等问题，变成原函数的导函数的零点问题；原函数的不等式问题，同样也变成了，通过导函数看单调性的问题。这里把这几个题，放在一起看，更加直观：例6.13，例6.4，这里变回原函数有几种手段，一种是我们直接看出来了，还有的可能是要用变限积分来转换

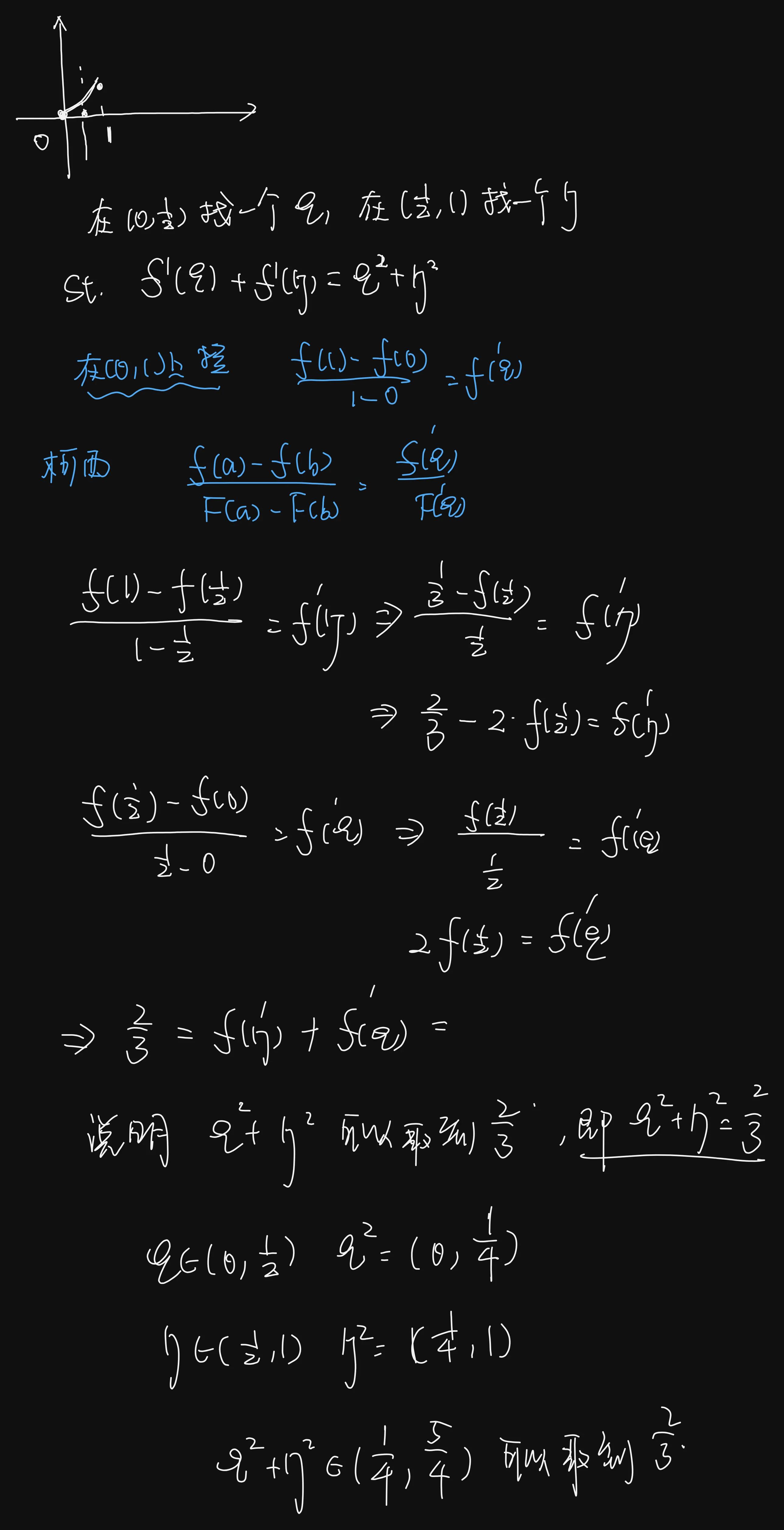
像我上面这种做法，我感觉是非常不严谨的，甚至说可以是错的

解

[!done]-
解此类题,一般可从要证明的结论出发,构造辅助函数.

拉格朗日中值定理 若函数 在 上连续,在 内可导,则在 内至少有一点 ,使等式

成立.

(证) 构造辅助函数 ,则 在 上连续, 内可导, . 于是,所要证的结论变为 “存在 ,使得 . ”

首先,由题设,有 .

分别在 和 上对 使用拉格朗日中值定理可得,存在 ,使得

由 (1) 式,得 . 又因为 ,所以 , 即 .

(注) 本题中, 的取值区间是由条件给定的,这给予了我们解题的方向,我们稍作思考便能得到分别对区间 和 上的 使用拉格朗日中值定理的思路. 若取消这个条件, 则解题难度会变大. 那么, 如何寻找划分区间的点呢?

假定 是我们要找的划分区间的点,分别对 上的 使用拉格朗日中值定理,可得存在 ,满足

要得到 ,即要得到

易由 解得 .