题20
题目
[!question]+
计算二重积分
分析
[!NOTE]+
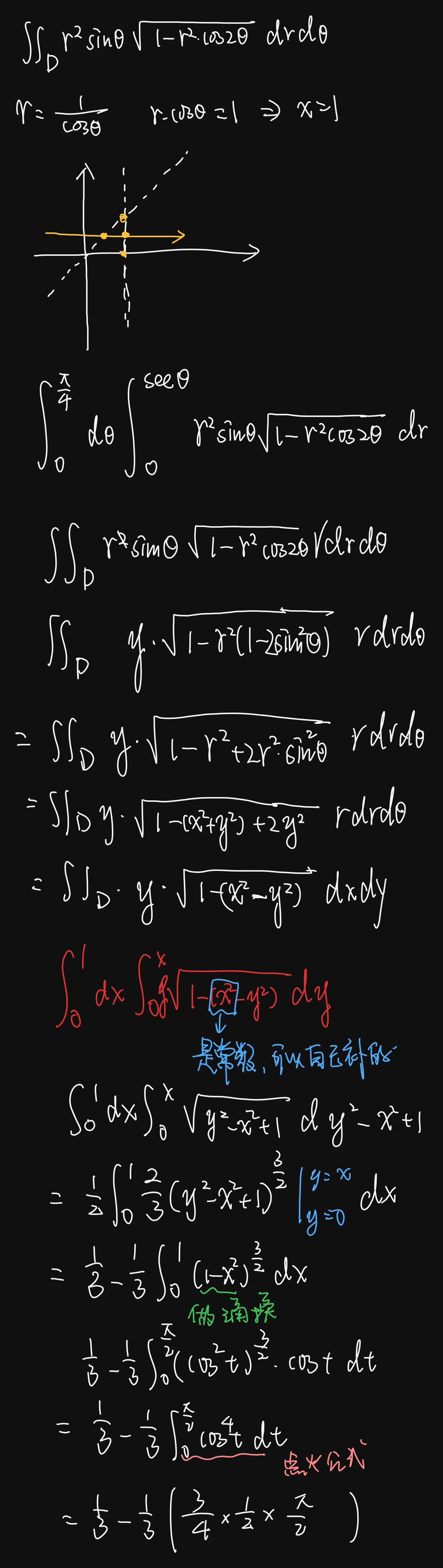
这样的二重积分,注意这里的x是常数,是可以自己在后面补项的
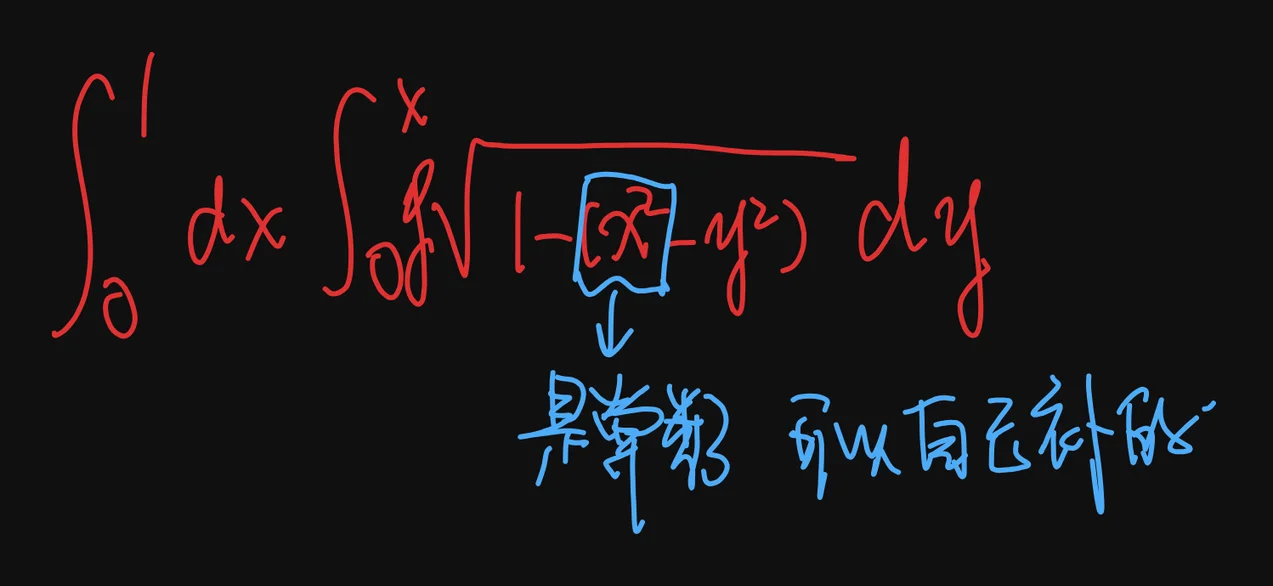
华里士公式如果是奇数次,到
解
[!done]-
本题中的二重积分是在极坐标系下给出的, 但稍作分析会发现它在直角坐标系下的区域表示较简单, 被积函数的表达式也较简单, 因而应选择在直角坐标系下进行计算.
解 在极坐标系下,积分区域
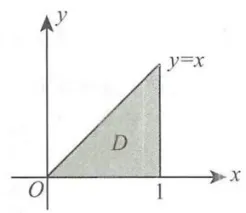
由
因此,
注 ① 很多时候, 我们都是对直角坐标系下给出的二重积分作极坐标变换以简化计算, 而本题恰恰相反. 本题中, 直接在极坐标系下计算题给二重积分较难, 而在直角坐标系下计算较简单. 这提醒我们, 在解题时, 切忌养成“思维定势”, 要学会针对具体问题进行分析.
② 本题用到了下面的定积分计算公式.
其中,正整数