题18
题目
[!question]+
一个高为
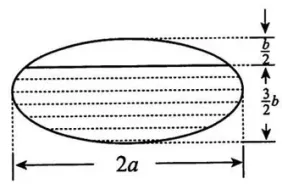
分析
[!NOTE]+
属于二重积分的应用,这里要记得椭圆的面积公式:
然后我们就只用算这部分近似于细长条的矩阵区域
解
[!done]-
解 以贮油罐的底面中心为原点,
由于油的密度为常量,贮油罐为柱体,故油的质量
设油面所占区域为
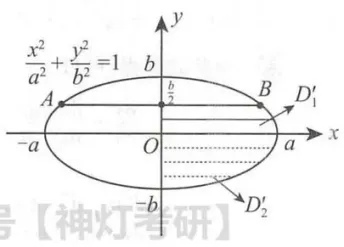
(法一) 利用定积分计算区域
记
根据椭圆面积公式,
将
因此,
(法二) 利用二重积分来计算
将区域
从而
其余同法一.
Jun 19, 20254 min read
[!question]+
一个高为

[!NOTE]+
属于二重积分的应用,这里要记得椭圆的面积公式:
然后我们就只用算这部分近似于细长条的矩阵区域

[!done]-
解 以贮油罐的底面中心为原点,
由于油的密度为常量,贮油罐为柱体,故油的质量
设油面所占区域为

(法一) 利用定积分计算区域
记
根据椭圆面积公式,
将
因此,
(法二) 利用二重积分来计算
将区域
从而
其余同法一.